This article is one of three papers to be presented exclusively on the web as part of the June 2000 JOM-e the electronic supplement to JOM.
	The following article appears as part of JOM-e, 52 (6) (2000), http://www.tms.org/pubs/journals/JOM/0006/Keavney/Keavney-0006.html JOM is a publication of The Minerals, Metals & Materials Society

Materials for Magnetic Memory: Overview

Characterizing Nanostructured Magnetic Materials with Photonic Probes

TABLE OF CONTENTS
INTRODUCTION VISIBLE-LIGHT PROBES X-RAY PROBES ACKNOWLEDGEMENTS References

New magnetic materials, especially nanostructured materials and thin films, continue to penetrate developing technological areas from magnetic sensors to microelectronics. In many of these applications, techniques for characterizing very small quantities of magnetic materials in novel configurations and environments are needed. The strong interaction between electromagnetic radiation, particularly visible and soft x-ray photons, and magnetic moments offers the ability to detect and characterize layers as they exist in device architectures with high sensitivity and element specificity. During the last ten years, a variety of visible light and synchrotron-based techniques have been developed for obtaining valuable spectroscopic and spin dynamical information from these materials. In this article, a few of these recent developments are discussed.

INTRODUCTION

The discovery in 1986 of oscillatory antiferromagnetic coupling in layered magnetic/nonmagnetic trilayer and multilayer structures,^1,2 and the subsequent discovery of the associated giant magnetoresistance (GMR) effect,^3,4 has led to increased interest in nanostructured magnetic materials for a wide range of applications. In addition, magnetic tunnel junctions (MTJs) have been successfully fabricated with even larger resistance changes.^5,6 The large room-temperature change in sample resistance in GMR and tunneling structures has dramatically expanded the potential of nanostructured magnetic materials for device applications⁷ such as magnetic sensors and high-speed, non-volatile magnetic random access memory (MRAM).⁸ Also, new materials with high magnetic anisotropy are of interest for magnetic recording media.

The realization of the considerable promise of these magnetic materials and structures has required the fabrication of thinner layers and new interfacial combinations that have not been made before. In many cases, lateral patterning of small features may also be necessary. The magnetic properties of most materials are often significantly affected by the reduction of dimensionality and by interfacing with other materials. Therefore, along with these new device architectures comes the necessity for characterization techniques with greater sensitivity, abilities for measuring materials in device-like environments, and capabilities for measuring various relevant material properties.

Due to the interactions that are possible between photons and magnetized materials, light-based probes offer the potential for high-sensitivity characterization. In the past decade, powerful synchrotron light source facilities have been constructed and instrumentation advances have been made that have stimulated the development of photon-based magnetic characterization techniques that provide information not available with bulk characterization techniques. This article discusses three such techniques, the new magnetic information they provide, and how this information is relevant to specific applications. Although these techniques were chosen as specific examples, progress has not been limited to these specific areas.

VISIBLE-LIGHT PROBES

In device architectures, magnetic layers can be as thin as a few Angstroms and buried under capping layers or other device component layers that may be hundreds of Angstroms thick. Since the mere presence of capping layers can modify magnetic behavior, this introduces the need to probe buried magnetic layers with very high sensitivity. Unfortunately, many of the most sensitive magnetic probes are based on spin-polarized electrons, and they can probe only the first few Angstroms beneath the surface. However, with visible light, the penetration depths can be a few hundred Angstroms, even for conductive films. This allows visible-light-based techniques to probe buried layers on thick substrates in a reflection or backscatter geometry. At the same time, the interaction of visible photons with metals is still strong enough to allow optical techniques to detect films in the monolayer thickness range.

Magneto-optical Kerr Effect

When polarized light propagates through a magnetized material, off-diagonal elements of the dielectric tensor can modify the polarization state of the light. This is manifested as a rotation of the primary axis of polarization (Kerr rotation) and a change in the ellipticity of polarization (Kerr ellipticity). The size of these effects can be related to the average sample magnetization through the matrix elements, which involve the magneto-optical constants. Therefore, if the polarization state of the incident light is known or prepared prior to incidence, the magnetization can be obtained by analyzing the polarization of reflected or transmitted light.

Figure 1. An experimental set-up for the longitudinal Kerr effect. The polarized laser beam is modulated by the photoelastic modulator (PEM) driven by a frequency generator, f. The reflected beam is analyzed and input into the detector. The lock-in technique increases the signal-to-noise ratio.

In practice, the typical magneto-optical Kerr effect (MOKE) experiment is performed in reflection geometry, with an externally applied field to allow hysteresis curves to be obtained. Depending on the preferred magnetic axis of the sample, the field may be perpendicular to the film plane, with the light at normal incidence (polar geometry) or parallel to the film plane, with the light incident at 20-30° (longitudinal geometry). The case for the longitudinal geometry is shown in Figure 1. The incoming polarization state is prepared to be either s- or p-linear polarization, and the reflected light is analyzed with an additional polarizer oriented to give the maximum intensity change per degree of polarization rotation.

The Kerr effect can easily detect magnetic films of only a few tens of Angstroms thickness and much thinner films with a little more work. Typically, a 10 mW He-Ne laser provides more than sufficient intensity, although some form of intensity stabilization is usually needed. A lock-in detection technique with an incident-intensity modulator is often used to improve the signal-to-noise ratio for very thin films. However, for films thicker than tens of Angstroms, even this may not be necessary.

MOKE is a technique that can be easily set up on a single optical bench and has sensitivity rivaling that of a SQUID magnetometer at a fraction of the cost. Since the Kerr effect requires only an external magnetic field and access to the sample for an optical beam, it also lends itself well to integration into a vacuum chamber for insitu measurements of evaporated or sputtered films, potentially even during deposition. However, one drawback of MOKE is that the relative contributions of magnetic material at varying distances from the surface can be difficult to model due to the absorption of the capping and magnetic layers. This problem can become even more acute in multilayered systems. Although this absorption behavior has been modeled by Zak et al.,⁹ MOKE is still most often used as a probe of hysteretic properties or relative magnetization trends, rather than as a quantitative measure of magnetization.

Spin-Wave Brillouin Light Scattering

In many cases, dynamical information from buried layers as well as magnetization data is needed. Magnetic excitations that can interact with visible photons (called magnons or spin waves) are present in magnetic solids. Because the energy spectra of these excitations are dependent on intrinsic material properties and are dramatically affected by nanostructuring the materials, they provide a powerful tool for magnetic characterization of magnetic thin films.

Brillouin light scattering (BLS) is an optical probe capable of detecting and determining the frequency of these excitations with high sensitivity. Although most incident photons scatter elastically, a very small fraction undergo inelastic scattering. In these inelastic events, photons may create or absorb collective excitations, such as phonons or spin waves; thus, the scattered photons are frequency shifted by an amount corresponding to the excitation energy of the phonon or spin wave. For magnetic characterization, the spin-wave excitations are the ones of interest and are selected by preparing the polarization of the incoming light beam appropriately. By determining the dependence of the spin-wave frequency and intensity on the external magnetic field and film thickness, the spin-wave spectrum is directly probed, yielding valuable information on the magnetic ordering of the films, as well as their uniformity and anisotropies. Because this technique uses optical photons as the probe, it is also well suited for both insitu measurements and for probing buried layers.

Figure 2. An experimental set-up for an in-situ, high-sensitivity BLS measurement in the backscattering geometry.

In practice, BLS is accomplished as shown in Figure 2. Because of the relatively small number of inelastically scattered photons and the closeness of the spin-wave modes to the primary laser line, the requirements on the performance of the optical system are extreme, especially for detecting spin waves in films only a few monolayers thick. The spin-wave frequencies can be as small as a few GHz, so the light source must have a line width of, at most, 20 MHz. Typically, a high power (~200 mW) laser is used--either an argon-ion at 514.5 nm or a diode-pumped, frequency-doubled neodymium-doped yttrium-aluminum-garnet (Nd:YAG) solid-state laser at 532 nm. In the BLS facility discussed here, a Nd:YAG laser with a linewidth of 2 MHz is used.

The solid-state laser is becoming more popular for this measurement due to recent improvements in the reliability, available linewidth and power, and the lack of need for water cooling at this power level. A polarization rotator allows selection of the incident linear polarization, and an acousto-optic modulator varies the intensity for a lock-in detection scheme. The laser beam is focused onto the sample to a relatively small spot size (~0.7 mm), and the backscattered light is collected via the collection optics, sent through a spatial filter for noise suppression, and then sent into the spectrometer for energy analysis. The incidence angle may be varied, especially for determining phonon spectra, although 45° is typical for spin-wave scattering.

For these measurements, the sample is in an external magnetic field oriented parallel to its surface and perpendicular to the optic axis. For spin-wave scattering, the analyzer is used to suppress the phonon modes, which otherwise would overwhelm the spin-wave modes. Even in the backscattering geometry shown here, the collected light will have a large elastic peak at the laser wavelength. Thus, to resolve the spin waves in the presence of this line, a spectrometer with very high sensitivity, stability, resolution, and contrast is needed. This is accomplished in the set-up described here using an actively stabilized six-pass tandem Fabry-Perot spectrometer developed by J.R. Sandercock,^10,11 as shown in Figure 2. The multipass geometry of this spectrometer gives very high finesse, and the single-transducer approach to the etalon scanning produces the exceptional stability needed for long counting times. This enables the BLS spectrometer to detect spin waves from films in the monolayer thickness regime.

Two Fabry-Perot etalons (FP1 and FP2) are arranged with their optic axes at an angle as shown, and the light to be analyzed is directed, using a mirror and two prisms, to pass through each etalon three times. This significantly enhances the contrast of the spectrometer over that of a single-pass Fabry-Perot. One mirror of each etalon is mounted on a scanning stage, which moves via a single piezoelectric transducer, and thus, the mirrors move together. Due to the angle q between the optic axes of the two etalons, the change in spacing of FP2 is less than that of FP1 by a factor of cos(q). This results in different spacings of their respective transmission orders, so that the two etalons tend to suppress each other's ghost peaks, thus removing ambiguity in assigning orders to the inelastic peaks from the sample.

After passing through the spectrometer, the light is incident on a detector, usually a high-quantum efficiency photodiode or a photomultiplier tube. The count rate from this detector is input to a multichannel scaler (MCS)-equipped data acquisition computer, which also controls the etalon scanning stage. The data obtained are, therefore, of backscattered intensity vs. frequency shift, Dw.

The analysis of BLS data can be somewhat complicated, depending on the sample geometry and the relative importance of the various terms that may contribute to the spin-wave energies. In this article, a few cases of importance to single films are discussed; spin-wave excitations in more complicated structures, such as coupled layers or superlattices, have been treated in other reviews dedicated primarily to light scattering.^12-14

In thin-film materials there are two types of spin-wave modes: bulk (or uniform) and surface (or called Damon-Eschbach) modes. The bulk modes may propagate at an angle to the film plane, and the perpendicular component of the wave vector is quantized. The surface modes propagate in-plane and are evanescent with distance from the surface. Both of these modes are solutions to the general continuum equations of motion for a material with magnetization M^15-17

where g is the gyromagnetic ratio, and H_eff may include contributions from external and demagnetizing fields, as well as effective exchange and anisotropy fields. Here, we consider the case of a single magnetic layer of thickness d with in-plane magnetization M and an in-plane external field H₀, neglecting anisotropy and exchange.¹⁸ For the bulk modes, this solution yields the dispersion relation

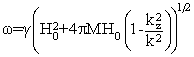
where k_z is the perpendicular component of the spin-wave vector k. For the surface modes,

where k_{| |} is the magnitude of the in-plane component of the spin-wave vector. For very thin films (k_| |d<<1), the surface-mode frequency approaches that of the lowest order (k_z = 0) bulk mode. In some cases, anisotropies can be included in the approximation above by adding an effective field to H₀. For volume anisotropy when the external field is along an easy axis, this term is H_an = 2K_V/M₀, where K_V is the volume-anisotropy constant. To include surface anisotropy and for the case where the external field is not along an easy axis, the analysis should be treated according to References 17 and 19.

In a typical BLS characterization, the primary quantities obtained are the spin-wave peak position and its dependence on the external magnetic field, film thickness, sample temperature, or other parameters of interest. These data are fitted to obtain the film properties. In addition, the spin-wave line width can provide at least qualitative information about the magnetic uniformity of the sample, and large backscattered intensity variations can indicate the increased magnetic fluctuations at phase transitions.

Figure 3. Spin-wave frequency vs. in-plane applied magnetic field for a 4 ML thick cobalt film buried under 35 Å of gold.

Spin-wave Brillouin scattering has been used to examine many properties of thin magnetic films.^20-22 Figure 3 plots the dispersion behavior of the surface spin-wave mode in a 4 ML thick cobalt film buried under ~35 Å of gold.²⁰ Note that the signal-to-noise ratio is quite good even at this low thickness. In fact, BLS is capable of detecting spin waves even down to 1 ML of cobalt with acceptable statistics.²³ In this respect, BLS outperforms even the most sensitive bulk magnetometers. Also, note that the field dependence is nonmonotonic (i.e., the mode frequency drops to zero at a critical field H_C of about 2 kOe). Associated with this dip is an increase in mode intensity, indicating a magnetic phase transition. In this case, the transition is the reorientation of the film magnetization from out-of--plane to in-plane by the external field.

By fitting the dispersion relation of Figure 3 to a model that includes any relevant anisotropies, the anisotropy energies, saturation magnetization, and gyromagnetic ratio for this film can be derived. In this case, first- and second-order uniaxial terms K_u⁽¹⁾ and K_u⁽²⁾ were used to model the perpendicular anisotropy. The solid line is a fit including the second-order term, and the dashed line is the result for K_u⁽²⁾ = 0. Therefore, this term clearly must be included to explain the spin-wave dispersion behavior. In addition, the fits show that the dispersion behavior is consistent with the perpendicular magnetization model. The perpendicular anisotropy constants were shown to increase with decreasing cobalt thickness in Reference 20, indicating that their origin is an interfacial perpendicular anisotropy.

X-RAY PROBES

Many current and anticipated applications for magnetic materials involve heterostructures or alloys that contain more than one magnetic component. This makes it difficult, or impossible, to determine the magnetic behavior of each component using the traditional bulk characterization methods. To accomplish this, a means of determining element-specific magnetic behavior in a thin-film sample is needed. The transition-metal K or L edges and the rare-earth M edges are sufficiently narrow and far from each other that element-specific x-ray absorption spectroscopy (XAS) can be easily accomplished. Therefore, polarized x-ray absorption techniques using new synchrotron beamlines as light sources offer the ability to selectively excite each spin subband and determine its absorption characteristics. Differences in absorption between orthogonal polarizations reflect differences in the conduction band spin-up and spin-down densities of states, and a wealth of information on the magnetic moments can be extracted. Here, the case for circularly polarized x-rays is mainly treated, because much of the early development of this technique^24,25 and the first use of dichroism for element-specific magnetic hysteresis²⁶ was with circular polarized light. However, dichroism is also possible with linear polarization.

X-ray magnetic circular dichroism (XMCD) is the spin-dependent absorption of circularly polarized x-ray photons by core levels in ferromagnetic materials. In standard (non-spin-dependent) XAS, photon absorption excites a core level electron to the valence band, so that the absorption probability is dependent, in part, on the density of states at the Fermi level. If the incident photons are circularly polarized, only spin up or down electrons will be excited, depending on the direction of the helicity of the light with respect to the absorbing atoms magnetic moment. In ferromagnetic materials, the density of states at the Fermi level is spin-dependent. Therefore, a difference in absorption is expected for left- and right-circularly polarized light incident on ferromagnetic materials. This difference in absorption can be related to the average magnetic polarization of the absorbing atomic species and can, therefore, indicate element-specific magnetizations. Consequently, XMCD has been used to probe magnetic properties in multilayers systems,^26-29 alloys,³⁰ and intermetallic compounds^31,32 involving both transition metals and rare earths. More recently, resonant-scattering techniques based on XMCD have been applied to layered systems to obtain magnetic switching behavior³³ and magnetic roughness information.³⁴

XMCD requires an intense source of circularly polarized light tunable in the energy range of interest for magnetic materials. For the L edges of the transition metals and the M edges of the rare earths, this is between 300 eV and 1,000 eV. If transition-metal K edges are used, energies above 1,000 eV are needed. In practice, therefore, XMCD requires a synchrotron source. Two types of light sources exist at synchrotrons--bending magnets and insertion devices--and both are suitable for generation of the required circularly polarized x-rays. On bending magnet beamlines, circular polarized light of either helicity is available, at reduced intensity, above and below the synchrotron orbital plane. The degree of polarization available in this arrangement is typically 80-90%. Insertion devices, such as undulators or wigglers, offer some advantages over bending magnet beamlines, although at higher cost. For an example of an undulator designed to produce polarized x-rays in the energy range important for transition metal L-edges, see Reference 35. The polarization is controlled by varying the relative phase between rows of magnets; therefore, the device may be specifically designed to allow an arbitrary polarization state. The polarization also may be changed without having to physically move any beamline components, as opposed to the bending magnet case. Finally, higher degrees of polarization (up to ~98%) are available, and more of the beam intensity goes into polarized light.

Figure 4. A schematic of an XMCD beamline. For photon energies in the transition-metal L-edge regime, the monochromator is typically a grating. Detectors for the three types of absorption measurements (transmission, fluorescence, and partial electron yield) are shown. In addition, total electron yield measurements can also be accomplished by monitoring the photocurrent from an isolated sample.

Figure 4 is a schematic beamline arrangement for XMCD measurements. The broadband beam from the insertion device or bending magnet is monochromated by a grating monochromator, which is used to scan the incident photon energy over a suitable range, depending on the transition being examined. The sample sits at the focus of the monochromatic beam, oriented such that its magnetization is as close to parallel to the beam direction as possible. The sample may be measured in remanence or there may be an external field to saturate it or to scan the field for hysteresis measurements. The absorption is measured as the incident photon energy is scanned through the relevant edge by the monochromator. The difference in spin-dependent absorption is obtained by taking spectra with both light helicities or by reversing the sample magnetization, if possible. The MCD signal is then the difference of these two spectra.

The absorption is typically measured by one or more of three ways. In total or partial yield measurements, the photocurrent, which is a measure of the total absorption, is monitored. Alternatively, the fluorescence yield from transitions of excited atoms back to the ground state can be measured. This yield also will be dependent on the absorption probability. Finally, if the sample is thin enough, the total transmitted intensity can be measured. The first two techniques can be used on thick samples, but are subject to surface sensitivities and saturation effects that can render the data analysis described quite complicated.

The spin-dependent absorption probabilities are governed by quantum mechanical selection rules for the transitions in question; therefore, these probabilities can be calculated. By applying the selection rules to either the itinerant magnetic transition metals or the more localized rare earths, sum rules have been derived that predict the MCD intensities for both cases. By applying these rules, one can also extract spin³⁶ and orbital³⁷ moments from the MCD data. For the case of the 3d transition metals at the L edges, the sum rules are

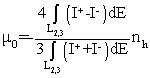
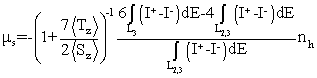
where m_o and m_s are the orbital and spin moments, I^+(-) is the spin-dependent absorption with the photon helicity parallel (antiparallel) to the magnetization, n_h is the number d-band holes per atom, and <S_z> and <T_z> are the spin and magnetic dipole operators. The integrations are performed over the indicated L edges. Some of these quantities may not be known for a given material; however, the <T_z> contribution for the 3d ferromagnets is small.^38-40 Also, by working with orbital-to-spin or total moment ratios, rather than absolute moments, uncertainties in n_h are removed.

Element-specific magnetic hysteresis using XMCD was reported on an Fe/Cu/Co trilayer film²⁶ in 1993. In this experiment, the relative MCD intensities at the iron and cobalt L₃ edges were monitored while an in-plane external magnetic field scanned the hysteresis curve of the sample. These separate signals indicate individual hysteresis curves of the iron and cobalt layers, respectively. These curves could then be used to explain features in the bulk hysteresis that were not separable by conventional magnetometry.

ACKNOWLEDGEMENTS

We thank the U.S. Department of Energy grant DE-FG02-93ER45488 and the U.S. Air Force Office of Scientific Research/DURIP grant F496209910147 for research support.

References

1. P. Grunberg et al., Phys. Rev. Lett., 57 (1986), p. 2442.
2. S.S.P. Parkin, N. More, and K.P. Roche, Phys. Rev. Lett., 64 (1990), p. 2304.
3. M.N. Baibich et al., Phys. Rev. Lett., 61 (1988), p. 2472.
4. H. Sato et al., Superlattices and Microstructures, 4 (1988), p. 45.
5. J.S. Moodera et al., Phys. Rev. Lett., 74 (1995), p. 3273.
6. T. Miyazaki and N. Tezuka, J. Magn. Magn. Mater., 139 (1995), p. L231.
7. G.A. Prinz, Phys. Today, 48 (1995), p. 58.
8. S. Tehrani et al., IEEE Trans. Mag., 35 (1999), p. 2814.
9. J. Zak et al., Phys. Rev. B, 43 (1991), p. 6423.
10. J.R. Sandercock, Solid State Commun., 26 (1978), p. 547.
11. R. Mock, B. Hillebrands, and J.R. Sandercock, J. Phys. E, 20 (1987), p. 656.
12. P. Grunberg, Light Scattering in Solids V: Superlattices and Other Microstructures, ed. M. Cardona and G. Guntherodt (Berlin: Springer, 1989), p. 303.
13. C. Patton, Phys. Rep., 103 (1984), p. 251.
14. S. Demokritov and E. Tsymbal, J. Phys.: Condens. Matter, 6 (1994), p. 7145.
15. M.G. Cottam and D.J. Lockwood, Light Scattering in Magnetic Solids (New York: Wiley, 1986).
16. T. Wolfram and R.E. De Warnes, Prog. Surf. Sci., 2 (1972), p. 233.
17. G.T. Rado and R.J. Hicken, J. Appl. Phys., 63 (1988), p. 3885.
18. R.W. Damon and J.R. Eshbach, J. Phys, Chem. Solids, 19 (1961), p. 308.
19. J.F. Cochran and J.R. Dutcher, J. Appl. Phys., 63 (1988), p. 3814.
20. A. Murayama et al., J. Appl. Phys., 82 (1997), p. 6186.
21. A. Murayama et al., J. Appl. Phys., 83 (1998), p. 613.
22. A. Murayama et al., Phys. Rev. B, 60 (1999), p. 15245.
23. A. Murayama et al., J. Appl. Phys., 85 (1999), p. 5051.
24. G. Schutz et al., Phys. Rev. Lett., 58 (1987), p. 737.
25. C.T. Chen, Nucl. Instrum. Methods Phys. Res. Sec. A, 256 (1987), p. 595; also in C.T. Chen and F. Sette, Rev. Sci. Instrum., 60, 1616 (1989); C.T. Chen, Rev. Sci. Instrum., 63 (1992), p. 1229.
26. C.T. Chen et al., Phys. Rev. B, 48 (1993), p. 642.
27. C.T. Chen et al., Phys. Rev. B, 42 (1990), p. 7262.
28. Y. Wu et al., Phys. Rev. Lett., 69 (1992), p. 2307.
29. J.G. Tobin, G.D. Waddill, and D.P. Pappas, Phys. Rev. Lett., 68 (1992), p. 3642.
30. Y.U. Idzerda et al., J. Magn. Magn. Mater., 127 (1993), p. 109.
31. D.J. Keavney et al., Phys. Rev. B, 57 (1998), p. 5291.
32. J. Chaboy et al., J. Magn. Magn. Mater., 140-144 (1995), p. 1051.
33. J.W. Freeland et al., Appl. Phys. Lett., 71 (1997), p. 276.
34. J.W. Freeland et al., J. Appl. Phys., 83 (1998), p. 6290.
35. S. Lidia and R. Carr, Nucl. Instrum. Methods Phys. Res. A, 347 (1994), p. 77.
36. P. Carra et al., Phys. Rev. Lett., 70 (1993), p. 694.
37. B.T. Thole et al., Phys. Rev. Lett., 68 (1992), p. 1943.
38. C.T. Chen et al., Phys. Rev. Lett., 75 (1995), p. 152.
39. R. Wu and A.J. Freeman, Phys. Rev. Lett., 73 (1994), p. 1994.
40. R. Wu, D. Wang, and A.J. Freeman, Phys. Rev. Lett., 71 (1993), p. 3581.

David J. Keavney is an assistant research professor and Charles M. Falco is the chair of condensed matter physics and professor of optical sciences at the University of Arizona.

For more information, contact D.J. Keavney, Optical Sciences Center, University of Arizona, Gould-Simpson Building 1015, P.O. Box 210077, Tucson, Arizona 85721; e-mail keavney@u.arizona.edu.