This article is one of five papers on computer tools for materials to be presented exclusively on the web as part of the April 1997 JOM-e—the electronic supplement to JOM. The coverage was developed by Steven LeClair of the Materials Directorate, Wright Laboratory, Wright-Patterson Air Force Base. Please tell us know what you think by taking the survey below.
	The following article appears as part of JOM-e, 49 (4) (1997), http://www.tms.org/pubs/journals/JOM/9704/Goraya/ JOM is a publication of The Minerals, Metals & Materials Society

Metal-Casting Process Design: Postmortem and Predictive Troubleshooting

It is possible to construct useful multimedia associative memories for troubleshooting, in the performance of industrial tasks, relying on the concept of self-organization and mapping of experiences. This paper demonstrates this concept for some aspects of metal casting. The theoretical issue is the question of whether it is possible to cluster and map in semantic vector spaces automatically, with little or no prior knowledge of the problem domain. The paper also reports on some early positive research results. Clustering is clearly feasible and useful, even when features are linguistic symbols rather than numerical ones. The clustering technique is demonstrated (via example and a downloadable program) for the storage and retrieval of part designs. Mapping seems to be feasible if there is, indeed, an implied relationship.

INTRODUCTION

This paper presents a variation on the practice of clustering objects that are described in terms of linguistic symbolic attributes in a semantic vector space. The technique does not require additional domain-specific information, it works directly with the symbolic attributes of objects, and it incorporates a new distance metric based on set operations. A hierarchical clustering technique can be used to discover detailed relationships between objects. Then, a search technique can be utilized for both predictive and post-mortem troubleshooting by using the clustered structure to retrieve similar objects, experiences, or events. These techniques for organization and searching can be applied in any domain comprising symbolic information. The objective this work is to utilize a self-directed process to extract information from a knowledge base of objects described with linguistic symbolic attributes. This information primarily includes the nature of the relationships between objects.

CLUSTERING AND SEARCH TECHNIQUES: A BACKGROUND

Clustering is the process of forming meaningful groups of data in multidimensional space such that the members in each resulting group possess a high degree of similarity to each other and yet are significantly different from members of other groups. Clustering has two major applications: discovering relationships in data and compressing voluminous amounts of data. The insight gained from the resulting structure can be captured and stored for future use. In order to use clustering for data compression, the distinguishing characteristics of each group are identified and captured in terms of attributes. Then, each group can be depicted by a single entity, called the centroid, composed of these attributes. This cluster structure can be analyzed with significantly less effort and time than required for the entire set of data. The procedures for clustering numerical data are relatively straightforward and are usually well-accepted, primarily owing to their crisp mathematical descriptions. The process is generally as follows. The objects to be clustered are denoted as vectors, where the dimensionality of the vectors corresponds to the number of attributes of an object. The data are normalized to ensure a consistent representation for all objects. A suitable hierarchical or nonhierarchical structure is selected. The next step is to choose an agglomerative or divisive procedure. Then, a method for merging or separating objects is selected from among linkage methods, centroid methods and variance methods. The clustering procedure can be accomplished using techniques that are graph-theoretic, probabilistic, or statistical or from artificial intelligence (AI)-inspired adaptive or rule-based algorithms. After clustering, numerous techniques, ranging from statistical to AI based, can be applied for cluster analysis. The latter are generally used when all other methods fall short of providing adequate results or when the data are non-numeric. Conceptual Clustering Conceptual clustering is a technique for grouping symbolic features with the objective that the clusters will be described by simple formulas from predicate calculus. The technique is based on the premise that not all attributes of objects are equally important.1 Therefore, in each cluster, objects are similar to each other in the sense that they score similarly on the "important" attributes. Different clusters are expected to have descriptions with different values of the selected important attributes. For example, symbols "train" and "truck" should be conceptually closer as compared to "airplane" in the context of transportation. When knowledge about the relative importance of attributes is not readily available, conceptual clustering is generally not meaningful. This approach does circumvent the problems associated with encoding data into numerical representation and standardization. However, it requires significant amounts of pre-processing in terms of time and effort. This adds to the computational complexity, and consequently, the run time of the clustering program. Optimal results can require NP-complete (nondeterministic polynomial time complete) algorithms.2

The use and application of this technique in the domain of metal casting, where the objects are descriptions of designs of metal parts. The idea is that the clustering technique can be used to discover relationships between a large base of previously designed parts. Then, when designing a new part, the engineer can query the system for parts designed in the past that are similar to the current design. The information contained in the part descriptions can then be used for predictive troubleshooting, to discover potential defects that can occur. In addition, in the case of a defective part that has already been cast, the search technique can be used for postmortem troubleshooting, to uncover solutions that were utilized in the past to fix parts with similar defects. In this manner, potential problems can be corrected before they occur, and existing problems can be solved quickly, thereby saving both time and money.

A NEW APPROACH FOR CLUSTERING AND SEARCHING

The Distance Metric

The distance metric is derived as follows:

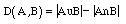(1)

Where D(A,B) denotes the distance between A and B. "|.|" denotes cardinality of a set; "u" denotes union, and "n" denotes intersection operations on sets.

If object A has "a" number of unique attributes and object B has "b" number of unique attributes, and they share "c" number of common attributes, then the distance between object A and object B is as follows:

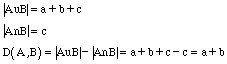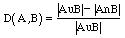(2)

Proof of the New Distance Metric

1. D(A,B) = D(B,A)
2. D(A,B) 0
3. D(A,B) = 0 if, and only if, A = B
4. D(A,B) + D(B,C) D(A,C)

1. Operations on sets are order independent. Therefore, D(A,B) = D(B,A).
2. |A u B| is always greater than or equal to |A n B|, then |A u B| - |A n B| 0. Therefore, D(A,B) 0
3. If A = B, then A and B represent the same set of attributes, and |A u B| = |A n B|. Therefore, D(A,B) = 0. If D(A,B) = 0, it means that |A u B| = |A n B|; therefore, A = B.
4. Consider three objects as shown in Figure 1, which demonstrate

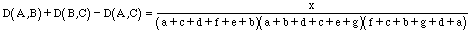(3)

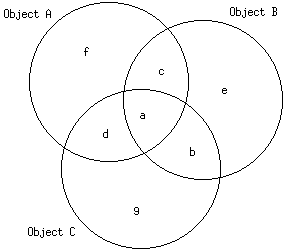Figure 1. Three objects. Letters represent the number of attributes in the regions. The distances between objects are as follows:

The numerator, x, of Equation 3 is a very large sum, but it only contains positive terms. Therefore,

D(A,B) + D(B,C) - D(A,C) 0, and D(A,B) + D(B,C) D(A,C)

Based on these criteria, the measure described in Equation 2 can serve as a distance metric. Because this distance metric uses set operations to compute the distance between two objects, each object within a data set can have a different number of attributes, and the attributes can be in any order. Furthermore, since set operations are used, which consider each item in the set as equally important and independent, the symbolic attributes of the objects are also considered as equally important and independent.

A New Method for Defining a Cluster Center

Hierarchical Clustering

Therefore, a hierarchical clustering approach is used for implementation. When the clustering procedure begins, a large cluster radius is used to discover the coarse relationships among objects. Then, each large cluster is re-clustered using a smaller cluster radius. This step is repeated recursively until some preset minimum radius is met. Following this approach, detailed relationships among clusters are discovered. The result is a tree-like structure of clusters, where the clusters closer to the root are larger. The sub-clusters then have successively smaller radii, with objects becoming more similar at deeper levels of the cluster tree.

There is no prespecified number of clusters. A new cluster is formed whenever an object is presented for classification that does not belong to any of the existing clusters. The sole member object in this new cluster also acts as the cluster-center, until new objects join the cluster. This clustering method is called the follow-the-leader approach. Whenever a new object joins a cluster, the cluster center is shifted to reflect the influence of the new member. This leads to the possibility that a previous member may no longer belong to the cluster. As new clusters are dynamically added, certain members may then qualify as members of other clusters.

This approach tends to bias the cluster formation by favoring the objects towards the front end of the data. In other words, the cluster formation is influenced by the order of presentation of the objects. Therefore, in this procedure, all the objects in the data set are presented repeatedly, until either no additional objects change clusters or alternatively, if a pre-specified number of iterations has been reached.

Search Technique for the Clustered Structure

In order to find the cluster closest to the cue with the new search technique, the hierarchically structured cluster tree is searched starting at the root. At each level of the tree, the cluster closest to the cue is identified. The search is then continued down that branch of the tree, with the closest cluster as the root. This procedure continues until the desired level of similarity is reached. At that level of the cluster tree, the closest cluster to the cue is considered to have the similar objects.

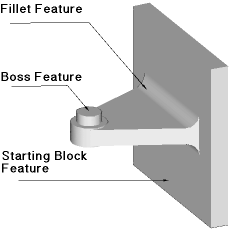Figure 2. A part illustrating geometric features. The image was sampled from a screen generated by the Rapid Foundry Tooling System, AI Ware, Inc.

In addition, after the closest cluster to the cue is identified, the adjacent clusters, based on a nearest-neighbor table, are also considered as candidates for containing similar objects. The members of these clusters are collectively reported as the objects similar to the cue. In addition to locating similar objects, this search technique can also be used to find the object that is most similar to the cue—the best match. This can be accomplished by searching the individual adjacent clusters identified above, which covers the possibility that the best match may reside on the boundary of a neighboring cluster.

APPLYING THE NEW TECHNIQUES TO THE METAL-CASTING INDUSTRY

Figure 3. Clustering results of five designs. Design 1: top face pocket; front face pocket; left face pocket. Design 2: top face pocket; front face pocket; left face pocket; back face pocket; right face pocket. Design 3: top face pocket. Design 4: top face pocket; blind hole. Design 5: top face pocket; blind hole; bottom face pocket.	Figure 4. The left panel shows the hierarchical cluster tree. The right pane shows a list of the children of the currently selected node. The clusters are labeled with the design number of the metal parts and refer to the same parts indicated in Figure 3. (Click the figure for a larger view.)

The clustering technique is first used to organize a large knowledge base of previously designed parts. This clustering imposes a structure on the collection of design experiences in such a way that similar designs can then be easily retrieved. The designs can be retrieved based on several degrees of similarity, ranging from very similar to partially similar. The idea is that by looking at previously encountered similar designs and the steps taken to generate them, the user can learn from the past experiences of others.

Figure 3 illustrates an example of hierarchical clustering for five cast parts. Note that the designs do not have the same number of features, yet they form meaningful clusters. This strength is a result of the set-based metric. In conventional clustering, it would generally not be possible to cluster objects with different dimensions. Figure 4 shows a screen view of the cluster browser, which enables the user to study the hierarchical cluster structure tree. The user can traverse the tree and can also interactively customize the view by choosing from a number of viewing options. The right pane shows a list of the children of the currently selected node. In this example, the clusters are labeled with the design number of the metal parts and refer to the same parts indicated in Figure 3.

Figure 5. A predictive troubleshooting screen from a system designed with an intelligent memory based on new clustering and searching techniques. A large-scale animated version of the screen (1 MB), showing the program at work, can also be viewed. For Macintosh users, a demonstration verison of the program (725 KB) can be downloaded as an file that can be unstuffed, using Stuffit Expander, as a folder called "Troubleshooting." Be sure to read the "readme" file before attempting to use the program. A Power Macintosh is recommended, although the program should run on a 68000-based machine. In order to install and run the demonstration, you should have Around 5MB of free disk space A monitor that supports 832 x 624 mode System 7.1 and above 16MB of RAM NOTE: JOM assumes no responsibility for the reliability of this program.

In utilizing the past experiences of others, a system designed with an intelligent memory based on this new clustering and searching technique can be used for predictive troubleshooting as well as for the postmortem troubleshooting of defective castings. In the case of predictive troubleshooting, the intelligent memory can be used to point out potential defects that can occur, based on the information in the memory of past part designs. That is, after a new design has been entered, the intelligent memory can be searched, using the new search technique, to find similar parts. Then, by studying the design episodes associated with each similar part, specifically the defects that occurred based on similar designs, the user can uncover potential defects in the designs. He or she can then choose to correct these potential defects by studying the cures, associated in the intelligent memory, with the defect for that part. In this manner, the user can correct potential problems in the design phase before an actual part has been cast. Figure 5 shows the screen for predictive troubleshooting from a system designed with an intelligent memory based on the new clustering and searching techniques. The user interacts with this screen using a hypermedia interface.

The intelligent memory, utilizing the new symbolic clustering and search techniques, can also be used for postmortem troubleshooting. Specifically, if a defective part has already been cast, the user can again search the intelligent memory for parts that had the same defect. By studying these parts, the user can get information about how their defects were cured and can then apply that knowledge to solve the current problem. Using an intelligent memory based on symbolic clustering and search, existing problems can be solved faster and potential problems can be corrected before they occur, thereby saving both time and money.

References

For more information, contact T.Y. Goraya, Department of Management Information and Decision Systems, Case Western Reserve University, Cleveland, Ohio 44106; (216) 368-3914; fax (216) 368-3914; e-mail tyg@po.cwru.edu.

Will You Take a Short Survey?