This article is one of five papers on computer tools for materials to be presented exclusively on the web as part of the April 1997 JOM-e—the electronic supplement to JOM. The coverage was developed by Steven LeClair of the Materials Directorate, Wright Laboratory, Wright-Patterson Air Force Base. Please tell us know what you think by taking the survey below.
	The following article appears as part of JOM-e, 49 (4) (1997), http://www.tms.org/pubs/journals/JOM/9704/Thaler/ JOM is a publication of The Minerals, Metals & Materials Society

Autonomous Ultrahard Materials Discovery via Spreadsheet-Implemented Neural Network Cascades

Author's Note: A U.S. patent is pending on the creativity machine described in this article.

The application of random inputs to the internal architecture of a trained neural network allows us to interrogate the conceptual space contained therein. For instance, we may supply random inputs to a neural network trained to output the formulas of known chemical compounds of the form A_xB_y. The formulas emerging from such a network consist of not just the exemplars shown to it during training but also a broad range of plausible chemical compounds previously "unseen" by that network. We say that the network "imagines" or "invents" new materials that are beyond its experience (i.e., its training). Supervising this stream of potential chemical formulas with a second neural network, trained to recognize valuable potential chemical compounds, it is possible to capture the emerging discoveries and, thus, create libraries of totally new commercially and technologically useful materials. This paper describes the construction, function, and output of a preliminary chemical invention machine that proposes new ultrahard materials with the simple binary stoichiometry A_xB_y.

THE CREATIVITY MACHINE PARADIGM

As an example, Figures 1-3 depict the process of novel automobile design, showing the basic CM architecture (Figure 1), the egress of the IE's output vectors from the known conceptual space of automobile training exemplars (Figure 2), and the evolution and evaluation of the emerging designs (Figure 3).

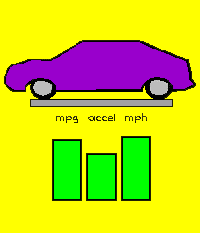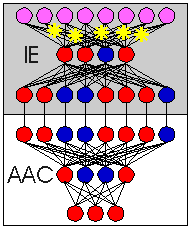
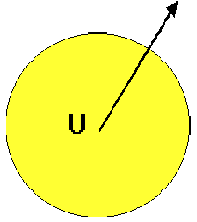
View Animation Figure 1. An IE that has "seen" examples of automobile shapes through training is exposed to internal chaos (yellow stars), causing it to produce a series of output vectors that represent plausible automobile designs. The supervising AAC network translates the imagined shapes to projected performance.	View Animation Figure 2. With increasing internal chaos, the IE's output vectors, representing candidate auto designs, become more radical. The emerging designs begin to deviate from those in the original training set, here symbolized by the conceptual universe (U). This egress from a known conceptual space may be generalized to any problem domain using a suitably trained ANN.	View Animation Figure 3. The supervising AAC network instantaneously evaluates each design for anticipated performance characteristics, filing away only those designs meeting some predetermined performance objective. In the case of general CM design, one can use an associative network to map the conceptual outputs of an IE to some measure of merit or related property. This critic network may then capture the most desirable of the emerging concepts.

Using this fundamental discovery paradigm, it is possible to interrogate the neural network model of any conceptual space, thus facilitating the quest for new discoveries, inventions, and solutions to seemingly intractable optimization and tailoring problems. As an example of applying the CM approach, this article focuses on the construction and function of a CM oriented toward the discovery of new ultrahard compounds having the formula A_xB_y. Following the above-mentioned template for CM construction, the process first involves exposing a feed-forward network to numerous examples of binary compounds and then, following training, subjecting its connection weights to successively higher degrees of perturbation. Emerging from this chaotic network would be a stream of potential chemical compounds, heretofore unseen by the network, yet possessing stoichiometrically plausible proportionalities of the elements A and B. A second network, trained to map chemical compounds A_xB_y to hardness values, could either cumulatively track the hardest of these compounds or create a vast survey of binary ultrahard materials.

It must be noted that this simple architecture may not be the most effective design, and that more complex variations on the CM paradigm may yield improved discovery capabilities. The enhanced cascade architecture may involve any number of highly interlinked IEs and AACs with noise strategically applied to select processing elements. In short, there is no way to avoid the involved architectural experimentation necessary to establish an optimal network structure. Thus, the technique presented here is given to spur the required rapid prototyping and testing environment needed to build and evolve such autonomous discovery systems while also serving to introduce the concept of the spreadsheet-implemented CM.⁵

THE SPREADSHEET-IMPLEMENTED CM

Exploiting the many analogies between biological neurons and cells within a spreadsheet, we may evaluate the state of any given network processing unit by way of relative references and resident spreadsheet functions (Figure 5). By referencing the outputs of such spreadsheet neurons to the inputs of other similarly implemented neurons, it is possible to create whole networks or network cascades. Unlike the algorithmic network simulation, all neuron activations are simultaneously visible and randomly accessible within this spreadsheet implementation. More like a network of virtual, analog devices, this simulation can be considered to be a distributed algorithm, with all neuron activations updated with each wave of spreadsheet renewal.

void feedforward(float *input, float *output) { for(j=0; j<nodes[lay]; ++j)     act[j]=1.0/(1.0+exp(-net[j])); }
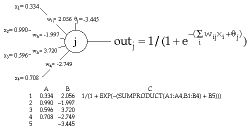Figure 4. Neuron activation within a given network layer is evaluated in C code.	Figure 5. A neuron implemented in a Microsoft Excel spreadsheet.

As a further benefit of the spreadsheet implementation, the user has a convenient graphical interface for constructing and experimenting with ANNs. For instance, one need only build a template neuron once, using simple copy and paste commands to build and connect whole networks from a prototypical processing unit. These procedures can be repeated on larger scales to move networks into position and link them into larger cascade structures. The resulting compound neural networks are transparent in operation and easily accessible for modification and repair. Furthermore, the approach lends itself well to the rapid prototyping of neural architectures when faced with multiple alternative neural circuitries.

In contrast to existing neural network toolboxes that allow for the cascading of multiple neural networks and generally represent a graphical interface to some underlying algorithmic source code (i.e., a DLL), the processing in the new ANN takes place strictly within the confines of the spreadsheet environment, with all processing units constantly accessible for various operator interactions and modifications. Thus, it is possible to readily involve various hidden-layer neuron interactions within the cascade function, to add various functional perturbations to select network weights, and to add recurrencies within any processing unit or groups of neurons. Furthermore, within sophisticated spreadsheet applications (e.g., Microsoft Excel) it is possible to enlist various resident functions and diagnostics, such as dependency traces among network cells and real-time plotting of network activation levels.

Because CMs require at least two ANNs linked within a cascade structure (Figure 1, for example), the spreadsheet implementation is the most natural construction technique. The IE and AAC inputs may readily be connected by relative cell references. Further, various forms of functional perturbations may be added to the constant connection weight values to optimize the generation rate of useful concepts. At all stages of construction, any resident Excel facilities may be enlisted to plot the behavior of any neuron or neuronal cluster or to perform various functional traces throughout the connectionist structure.

Excel’s resident macro utility, Visual Basic for Applications (VBA), typically drives the spreadsheet-implemented CM. Its chief functions are to administer random perturbations to individual neurons or connection weights within the IE, to enable any recurrencies within the CM architecture (i.e., Excel does not allow for self-referent loops), and to perform any run-time diagnostics of the machine.

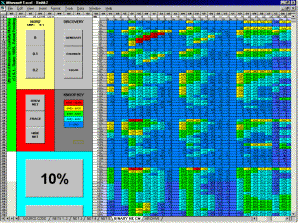
Figure 6. The Excel interface built for this study. Buttons to left activate various cascade functions; the colorized matrix to the right intuitively displays locations of ultrahard discoveries of interest.

Perhaps the spreadsheet implementation of the CM has its greatest advantage when the necessary cascade structure consists of many highly interconnected networks. For instance, various juxtapositional invention schemes require the use of several IEs running in parallel and patrolled by a single AAC.⁶ Alternatively, a number of independent AACs, each alert to the separate judging criteria of a single IE’s output, may be simultaneously active. Here, the ability to rapidly interconnect these various modular networks by relative cell reference tremendously expedites overall CM construction and debugging.

Excel, together with its VBA macros, allows the creation of very striking and easy-to-use interfaces. Figure 6, for example, presents the spreadsheet interface used in this materials study. Noise levels may be set in the upper left panel prior to any run. The CM runs may be initiated by the "generate" button. The hardness survey is then cumulatively displayed in the 100 x 100 colorized matrix to right, where anticipated Knoop hardness is predicted as a function of the constituent elements A and B. A similar matrix, included within the display, shows the anticipated stoichiometric ratios of A and B, in terms of an x/y ratio.

EXAMPLE OPERATION

View Animation Figure 7. An illustration of the generalized cascade feed-forward process (depicted for iron and oxygen): Random inputs are applied to networks 1 and 2, generating electron shell configurations for elements A and B, respectively. (Step 1: Iron and oxygen electron configurations are generated.) After applying a combination of the elements (A and B, determined in step 1), network 3 generates a recommended stoichiometry: x,y. As hardness values are calculated for each imagined compound, they are recorded within two 100 x 100 matrices—one yielding atomic composition and and one providing the ratios of x/y for the hardest stoichiometry found. (Step 2: Fe2O3 is recommended.) The candidate compound is applied to network 4, where small noise terms are added to the x,y inputs to generate an alternative stoichiometry: x',y'. In the animated sequence, the starbursts represent the introduction of random inputs or noise to specifc input nodes of the networks. (Step 3: Fe3O4 is recommended.) The alternative formula is passed to network 5, where the Knoop hardness of hardest potential phase of the compound is calculated. (Step 4: For Fe3O4, a Knoop hardness of 682 is calculated.)

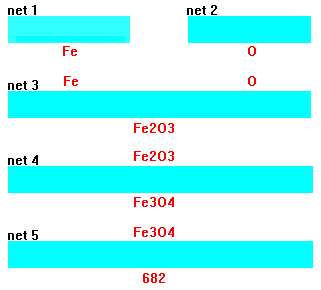
In the first stage of stoichiometry generation, four random numbers (three boolean numbers, representing a binary encoding of an element’s row in the Periodic Table, and one analog number, representing its column coordinate or chemical group) are supplied to each of two ANNs (networks 1 and 2 in Figure 7). For example, lithium would be represented with the input vector seed "0, 1, 0, 0.13," with the successive bits "010" representing row two of the Periodic Table, and 0.13 denoting that the element is found 13 percent of the way across the row. The outputs of these networks then yield elements A and B in an electronic representation, incorporating a similar binary-coded row along with the valence shell electron configuration via s, p, d, and f populations (row left bit, row middle bit, row right bit, s-electrons, p-electrons, d-electrons, f-electrons). Hence, networks 1 or 2 could produce the output "0, 1, 0, 1, 0, 0, 0" for lithium. Using such a representation for chaotically seeding networks 1 and 2, it is possible to rapidly and randomly generate representations of randomly chosen elements A and B without a need to look up tables or formulas for electron shell occupation. As Figure 7 shows, networks 1 and 2 randomly imagine various ground state electron configurations for elements A and B, respectively.

Once networks 1 and 2 imagine candidate elements A and B (inert gases were rejected by the driving algorithm), the respective electron shell configurations pass to network 3, which maps an anticipated or approximate stoichiometry x and y. The training exemplars for this network consisted of 200 binary compounds chosen randomly from standard chemical references. Therefore, if only Fe₂O₃ had been shown to the network as a training exemplar, the network would predict 2 and 3 for x and y, respectively. Alternatively, had the network been exposed to exemplars of both FeO and Fe₂O₃, the emerging subscripts predicted by network 3 would be averaged values for the observed subscripts—1.5 and 2, respectively. Thus, the intermediate formula recommended by network 3 produces a likely mean stoichiometry based upon the network’s previous chemical experience. By convention, if networks 1 and 2 yielded identical elements such as C and C, the recommended subscripts are 1 and 1.

Supplied with a representative stoichiometry from network 3, network 4 (an autoassociative network) invents some valid and, perhaps, creative alternatives for x and y. To understand how this process works, recall that within an ANN every stored memory, as well as generalizations of those memories, takes the form of so-called attractor basins. That is, if network 4 were made recurrent and some random seed were provided as inputs, the outputs would gravitate toward a memory of some stored exemplar, such as Fe₂O₃ or another plausible stoichiometry such as Fe₃O₄ (the network has imagined this new valence state of iron by generalization from other transition metal oxides). Upon multiple passes through this network, relaying outputs back to inputs, the outputs (or inputs) would progressively move toward some exact stoichiometry such as Fe₃O₄. Thus, the network falls into one of its attractor basins. This scheme allows us to roam through a number of plausible stoichiometric combinations unseen by the network, yet generalized from the chemical formulas of isoelectronic compounds. (In the operation of this particular cascade, the network was not made recurrent to speed processing. Therefore, stoichiometry was not quantitatively correct. Rather, it served as a rough approximation to yield an estimated or fuzzy ratio of x/y departing from the first stoichiometric guess offered by network 3.)

The final network within the discovery cascade, network 5, is trained to map the completed binary compound A_xB_y to a projected Knoop hardness value of the compound’s hardest possible phase. Training exemplars for this network were gathered from a variety of sources, including the CRC Handbook, minerological texts, and a number of references featuring hardness measurements for a variety of semiconductors and intermetallics. To make contact with the plentiful minerological examples, a separate network was trained to relate Moh’s scale hardness to Knoop hardness. Training data for the hardness mapping network was limited to high atomic number elements chosen exclusively from beyond the second row of the Periodic Table.

The chosen trainer for this problem was a special back-propagation trainer based on Microsoft Excel and known as Neuralyst^TM (download a zipped demo version). The root-mean square (RMS) training error was maintained below five percent of the range of output parameters. Testing error was maintained below five percent RMS for all networks involved. All networks employed full connectivity, with all processing units employing sigmoidal squashing functions. Following the training of each network, specially written VBA macros converted the connection weight matrix into linkable spreadsheet networks. Once cut and paste into their respective positions in the CM cascade, each was connected manually by relative reference between the required outputs and inputs.

Those spreadsheet cells representing noise inputs to the cascade structure were supplied with a resident random number routine called "rand()," thus achieving the perturbations necessary at the inputs of networks 1, 2, and 4, as shown in Figure 7. A governing looping algorithm was used to repeatedly drive the feed-forward propagation of noise through the spreadsheet network as well as to provide the interactive graphics used to control and monitor the Excel interface shown in Figure 6.

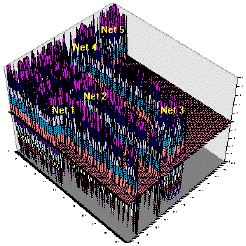View Animation Figure 8. Actual activation patterns across the spreadsheet as new ultrahard materials are imagined. The actual network modules, roughly located by the lavender ridges, are labeled to correspond to the networks depicted in Figure 7. The z-axis represents values appearing in spreadsheet cells, while the x and y coordinates represent rows and columns within the spreadsheet. In many respects, the rising and falling activation levels are reminiscent of cortical activity within the human brain. Analogous to the human internal imagery process, no new information is entering the system. All new information originates internally as a result of the application of noise to the cascade.

In operation, one may simultaneously observe the instantaneous activation level of all processing units of the cascade. Applying the resident Excel x,y,z plotting facility over the spreadsheet region representing the CM cascade, one may view the evolution of activation patterns across the the interconnected networks. This is illustrated by the animation in Figure 8, which comprises time slices of spreadsheet activation along with some general notion of network placement. Static topological features represent network weights and biases, while those in motion signify changing neuronal activations or noise inputs.

As the discovery process proceeds, the spreadsheet automatically logs the Knoop hardness of each binary combination of elements A and B, as well as the corresponding stoichiometric ratio x/y. Therefore, as the CM successively encounters harder stoichiometries of and elemental combinations of A and B, both hardness and the x/y proportionalities are updated within two matrices that appear as real-time displays in the spreadsheet. (Figure 9 depicts the evolution of the hardness matrix for a low atomic number.)

Noise inputs occur at two separate stages of the compound IE. In the first stage, noise input prompts the Monte Carlo generation of ground-state electron configurations of the elements A and B. The level of perturbation can be considered fixed for this process. In the second stage of stoichiometry generation, there is adjustability in the RMS perturbation level as applied to the autoassociative network so that the system may systematically depart from the most common stoichiometry recommended by network 3 toward a novel stoichiometry. Hence, the novelty, as well as the predictive risk, involved in generating new stoichiometries increases with the applied noise level at this stage of the cascade feed through. Therefore, within the spreadsheet discovery system, three levels of perturbation to the x and y inputs of network 3 are allowed for: RMS values of 0, 0.1, and 0.2, as compared to normalized inputs that may vary between 0 and 1. The results reported in this paper were carried out at the intermediate noise level of 0.1.

AUTONOMOUS MATERIALS DISCOVERY

In general, this scheme shares many of the characteristics of human-level discovery, including

1. A completely neuronal approach to learning and creativity, as in the human brain, which is a complex cascade of biological neural networks (i.e., the CM is implemented completely with a similar cascade of ANNs).
2. Learning through repeated interaction with the conceptual space (i.e., training the component ANNs).
3. The internal generation of creativity without the introduction of any additional information (i.e, the introduction of unintelligible noise drives the ANN cascade’s search). (Note: This observation has motivated me to explore the ubiquitous sources of noise within neurobiology as the inpetus and mechanism whereby human beings create and discover.)⁸

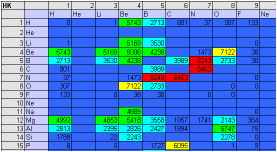View Animation View Hardness Survey of All Binary Compounds Figure 9. Operation of the binary ultrahard materials CM. In an uphill-climb process, the CM discovers successively harder stoichiometries and displays them in a 100 x 100 matrix (only low Z is shown here). Hardness values are color coded from the blue (the softest), to red (the hardest).

THE PREDICTION OF ULTRAHARD MATERIALS

P-Creativity

Table I. The Top 30 Predicted Ultrahard Binary Compounds Based on Projected Knoop Hardness (Hk)
Hardness Order	A	x	B	y	Hk
1	Be	6.000	Fr	1.060	8628
2	C	1.228	C	1.217	8623
3	B	1.391	O	1.689	8605
4	B	1.225	N	1.265	8575
5	Be	6.000	Cs	1.148	8546
6	C	1.239	N	1.262	8530
7	B	5.999	Cs	1.139	8526
8	B	6.000	Fr	1.076	8374
9	Mg	6.000	Fr	1.238	8288
10	B	5.462	Rb	1.330	8182
11	Au	4.453	Zr	5.999	8137
12	Al	6.000	Fr	1.109	8131
13	Be	5.921	Rb	1.448	8102
14	Pt	4.449	Zr	5.999	8040
15	Al	5.996	Cs	1.419	8032
16	Au	4.731	Mn	5.999	8025
17	Au	4.598	V	5.999	8004
18	Be	1.389	O	1.568	7953
19	Pt	4.591	V	5.999	7936
20	Au	4.424	Y	5.999	7909
21	Au	4.374	La	5.999	7903
22	Pt	4.720	Mn	5.999	7900
23	B	1.277	Yb	1.196	7896
24	Au	4.812	Fe	5.999	7859
25	Mg	6.000	Cs	1.774	7839
26	Pt	4.421	Y	5.999	7837
27	Au	4.546	Ti	5.999	7772
28	Pt	4.371	La	5.999	7759
29	C	1.227	Tm	1.186	7759
30	Pt	4.540	Ti	5.999	7750
View Spreadsheet Results for All Binary Compounds.

These p-creative materials discoveries include the following:

• C₃N₄ is predicted within the uncertainties of the stoichiometry generation with x/y = 1.239/1.262 = 0.98, rather than the anticipated 3/4 = 0.75. This compound may correspond to the recently proposed ultrahard material known as beta-C₃N₄.^9,10 Here, the CM predicts this compound to be an ultrahard material, somewhat softer than diamond. This result is consistent with recent findings in which beta-C₃N₄, at first theoretically predicted to surpass diamond in hardness, actually possesses an ionicity that reduces the bonding charge and, therefore, the bulk modulus.^9,10 Interestingly, it appears that the network cascade is generalizing the cases of Si₃N₄, just as its human counterparts did: C. Sung, then of Norton Corporation’s Diamond Technology Center conjectured as early as 1984 (in an abandoned patent application) that Si₃N₄ may exist in both the alpha and beta phases. Collaborating with Marvin L. Cohen of the University of California at Berkeley, a remarkably high theoretical bulk modulus was calculated.¹¹
• BN, assumed to be the cubic phase, was totally unknown to the CM before operation. The discovery cascade predicts the binary combination to be slightly enriched in nitrogen with x/y = 1.225/1.265 = 0.97. Although a well-known and commercialized ultrahard material, network 5 may slightly overestimate the material’s hardness due to sigmoidal activations implemented within the output node.
• C_xH (x > 6) appears as an ultrahard candidate, possibly a-C:H—amorphous, hydrogenated carbon in which 15 percent hydrogen, at most, is present. The real-time CM output shows that progressively higher x values result in increased values of hardness, with x saturating at a value of 6—the upper limit for any subscript within this simulation. This trend is consistent with what is generally known about amorphous carbon. As hydrogen content diminishes and carbon atoms are forced to form a three-dimensional network among themselves, both bulk modulus and hardness tend to increase.
• BeO is predicted to have a Knoop hardness near 8,000. The cascade anticipates an x/y ratio of 0.89 rather than 1.
• BC (x/y = 1.01) is predicted as very hard, having a Knoop hardness of 5,171; in the literature, the value for B₄C is 2,750.

H-Creativity

• FrBe₆₊ (in this application, the plus sign is essentially equivalent to a greater than/equal to sign)—although francium is an admittedly a short-lived material with a half-life of only 22 minutes, this compound is predicted to rival or surpass the hardness of diamond. The network prediction may stem from the increasing hardness trend among borides and beryllides containing successively heavier cations. If beryllium can form a network, as do the borides, with francium tightly filling the interstices, the incompressibility of the francium electron core would contribute substantially to bulk modulus and, hence, to hardness. CsBe₆₊, analogous to FrBe₆₊, could likewise form a nearly diamond-hard phase. With a smaller covalent radius, however, the cesium would not offer the same degree of lattice stiffening. The only precedent for theoretically predicted ultrahard beryllium compounds is an interpenetrating diamond-like network system of BeF₂/SiO₂ and its analog BeF₂/GeO₂, proposed by P. Hoffmann in 1992.¹¹
• B₂O₃, if successfully crystallized, could produce a phase that is comparable in hardness to diamond. Increasing the levels of noise in the CM yields greater hardness with increasing proportions of boron.
• CsB₆, FrB₆, and RbB₆ most likely have structures analgous to the LaB₆ network structure and are likewise predicted to approach diamond hardness, owing to the incompressibility of these large radius atoms in filling boron cages.
• Ultrahard intermetallics (e.g., Au₄Zr₅, Pt₄Zr₆₊, Al₆₊Cs, Au₅Mn₆₊, Au₅V₆₊, Pt₅V₆₊, Au₄Y₆, Au₄La₆₊, and Pt₅Mn₆₊) as well as a number of other intermetallics show the promise of significant hardness. Very little is known about the hardness of these speculative compounds, which have been extrapolated from the discovery cascade. Further analysis and training over more extensive training sets will be needed to understand and corroborate the results.
• Hydrogen-deficient polymers of boron and beryllium, analogous to the above-mentioned hydrogenated amorphous carbon, also hold promise as ultrhard materials (Figure 8).

ANTICIPATED IMPROVEMENTS TO THE DISCOVERY CASCADE

Another system pathology involves the IE's occasional generation of ions, radicals, and charge complexes. Therefore, in addition to producing species such as H₂O and H₂O₂, the IE proposes species such as H₃O⁺ and OH^-—materials attaining the equivalent of inert gas electron configurations. When such materials were generated, they were generally interpreted as existing in combination with other ions to achieve charge neutrality within the derivative crystal lattice.

Currently, a much more ambitious materials CM is under construction, incorporating an IE that checks for charge neutrality and thermodynamic stability for candidate species having as many as five distinct chemical elements. The IE has been trained with more than 10,000 inorganic compounds drawn largely from x-ray crystallographic databases. Generating hypothetical compounds with as many as six elements, this IE will serve to generate a dynamic database of potential chemical compounds. A cascaded associative network may simultaneously predict a wide range of chemical, physical, and, perhaps, medical properties for each of these emerging compounds, allowing us to tailor specific compounds to a variety of requirements.

CONCLUSIONS

The spreadsheet implementation of the creativity machine paradigm is most conducive to the rapid prototyping of the required network cascade architecture, allowing us to quickly experiment with alternative networks and interconnectivities, finally arriving at the highly successful architecture discussed herein. Encouraged by the cascade’s ability to rediscover both verified and theoretical ultrahard compounds, we tend to attach more significance to some of the more speculative predictions. Hopefully, some of these radical projections reflect very subtle trends within the relatively sparse training database and are, in fact, useful patterns that have evaded the scrutiny of researchers. Alternatively, these predictions may represent the thinking of an inadequately trained system that will require more of an apprenticeship period with the seasoned materials scientist before yielding completely accurate recommendations.

In the meantime, however, we may reliably use such creativity machines to provide educated guesses at regimes that will yield important materials breakthroughs.

ACKNOWLEDGEMENTS

References

For more information, contact S.L. Thaler, Imagination Engines, Inc., 12906 Autumn View Drive, St. Louis, Missouri 63146; (314) 576-1617; fax (314) 434-8591; e-mail sthaler@ix.netcom.com.

Will You Take a Short Survey?