 |
The following article is a component of the February 1998 (vol. 50, no. 2) JOM and is presented as JOM-e. Such articles appear exclusively on the web and do not have print equivalents.
|
Overview
Solidification Processing of Materials in Magnetic Fields
B.Q. Li
 |
|---|
| CONTENTS |
|---|
|
The use of external magnetic fields is now widespread in the metals and semiconductor industries to control the behavior of the melts during solidification, resulting in improved process performance and better quality products. With an applied magnetic field, a melt may be supported in air while being solidified by a well-shaped Lorentz force in place of a mechanical mold to obtain high-purity products. The field may also be configured to provide an environmentally friendly, yet effective means for melt stirring, which is useful in generating a desired melt mixing pattern during semiconductor crystal growth or producing a strong turbulent shear flow to induce grain refinement effects during metal casting. A direct current (d.c.) magnetic field can also be used to reduce unwanted turbulent flows and fluctuations associated with melt convection during solidification to help eliminate solidification defects. Because molten metals and semiconductor metals are electrically conducting, the same principles apply for the design of magnetically assisted solidification processing systems for both materials. The details of operation procedures and field control parameters, however, are different because of different technology development history and quality requirements. The attention of metal producers is presently focused on the adaptation of the existing technology to the new generation of casting processes. The semiconductor crystal growers, on the other hand, are actively pursuing electromagnetic stirring while searching for magnetic field configurations that render more effective damping effects in crystal growth.
Solidification describes the phenomenon of liquids transforming into solids as a result of a decrease in liquid temperature. It occurs in a wide range of industrial processes, including casting and semiconductor single-crystal growth.1-3 As liquids undergo solidification, fluid flow and turbulence occur in the solidifying liquid pool and have critical implications to both the solidification-process design and product quality control.1,2 There is extensive research devoted to developing a fundamental understanding of convective flows in solidifying melts and designing effective measures to control and optimize solidification-processing systems in order to obtain solidification products of high quality. One of the very useful methods that have been successfully applied to controlling melt convection in solidification systems is the use of magnetic fields.
The first attempt to deliberately apply magnetic fields to benefit solidification processing dates back to the early 1930s,4,5 and today the use of magnetic fields has become a standard industrial practice in the solidification processing of electrically conducting fluids such as molten metals and semiconductors.6-8 In general, magnetic fields may be configured to contain the melt in air while solidifying, to generate melt convection deep in the solidifying liquid pool, and to damp out the deleterious turbulence flows and fluctuations associated with melt convection. All of these effects have been explored in both metals and semiconductor industries, and improvements in both process control and product quality have been impressive.
Because molten metals and semiconductors behave the same in a magnetic field, the same principles apply in the design of their processing systems; however, the quality requirements for the two materials differ greatly. Generally speaking, quality issues concerning metal producers include grain-size uniformity, macro- and centerline segregation, and internal cracks and inclusions, among others; electronic crystal growers are concerned about impurity striation and radial and microscopic uniformity in crystals. This difference is reflected in the different details of operation control and field configurations used for the two materials.
The basic mechanism by which an applied magnetic field affects the solidifying melt may best be appreciated through the study of the Maxwell stress tensor T
 (SI unit) for a macroscopic homogeneous medium9
(SI unit) for a macroscopic homogeneous medium9
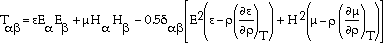 |
(1) |
where  is the electric permittivity, E
is the electric permittivity, E is the
is the  th component of the electric field, µ is the magnetic permeability, H
th component of the electric field, µ is the magnetic permeability, H is the
is the  th component of the magnetic field,
th component of the magnetic field,  is the density of the fluid, and T is the temperature. The Kroneker delta
is the density of the fluid, and T is the temperature. The Kroneker delta 

 takes the value
takes the value 

 = 1 if
= 1 if  =
=  and
and 

 = 0 if
= 0 if 

 , where
, where  ,
,  = 1, 2, 3.
= 1, 2, 3.
In Equation 1, the first and the third terms on the right-hand side represent the electrostatic effects. While electrostatic fields are rarely used during the solidification of conducting fluids, their use in affecting other types of phase-change processes such as boiling and condensation are common.10,11 The magnetic effects come from the remaining two terms. The last term represents the force resulting from the change of magnetic properties and has recently found applications in protein single-crystal growth, a rapidly growing area of great economic importance.12 The major effect of the applied electromagnetic field on metal and semiconductor solidification comes from the other two terms on the right-hand side.
For conducting fluids such as the molten metals and semiconductor melts, the magnetorestrictive effects are negligible [i.e.,  (
(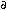 µ/
µ/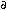
 )T
)T  0].9 Therefore, convection in the melt pool is influenced by the volumetric momentum source of the electromagnetic origin, the Lorentz force. The Lorentz force F is equal to the divergence of the Maxwell stress tensor
0].9 Therefore, convection in the melt pool is influenced by the volumetric momentum source of the electromagnetic origin, the Lorentz force. The Lorentz force F is equal to the divergence of the Maxwell stress tensor 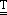 , viz.,
, viz.,
where T
 ,
, denotes the derivative of T
denotes the derivative of T
 with respect to
with respect to  .
.
With the magnetohydrodynamic form of the Maxwell equations,9 it is straightforward to show that Equation 2 reduces to the Lorentz force in a familiar form13
F = J x B = 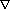 x H x B = x H x B =  (E + u x B) x B (E + u x B) x B |
(3) |
where J and B are the current density and magnetic-induction fields, respectively, and  is the electric conductivity. Also, to arrive at Equation 3, use has been made of Ohm's law for a moving conducting fluid
is the electric conductivity. Also, to arrive at Equation 3, use has been made of Ohm's law for a moving conducting fluid
J =  (E + u x B) (E + u x B) |
(4) |
Two types of magnetic fields are applied in solidification processes for molten metals and semiconductor melts. The first involves the application of alternating magnetic fields to generate eddy currents and, hence, the Lorentz force. For solidification conditions of practical interest, the term u x B is small compared with the induced electric field E; thus, the Lorentz force may be calculated as if the melt were a solid14-17
F =  E x B E x B |
(5) |
This force is exploited to generate strong flow motion near the solidification front to either shred out the newly formed dendrites (as for the metal-casting case) or to homogenize the solute concentration and smear other flow instabilities (as for the semiconductor crystal-growth case). It is also responsible for the support or shape of solidifying melts against gravity.
The second instance involves the use of static magnetic fields to reduce the fluid motion or local flow instability in the solidifying liquid pool. For an arbitrary magnetic field configuration, the Lorentz force is expressed by Equation 3, which entails the solution of the induced electric field that requires the fluid-field distribution. However, for a two-dimensional geometry with transverse magnetic field and/or axisymmetric magnetic field distribution with axisymmetric flow without swirling motion, a much simpler expression for Lorentz force can be obtained18-20
F =  u x B x B u x B x B |
(6) |
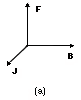
In this case, there is no need for the calculation of the electromagnetic field as B is an applied magnetic field; hence, the computational procedures are simplified considerably. The basic mechanisms for the two types of forces are schematically illustrated in Figure 1.
 |
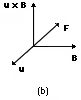 |
| Figure 1. Lorentz force F on a fluid element generated by two types of magnetic field: (a) the application of an a.c. electromagnetic field resulting in the Lorentz force F distribution that generates stirring in the melt, and (b) the application of a d.c. magnetic field gives rise to a force F distribution that opposes the local fluid velocity. Note that Figure 1b is based on Equation 5.
|
The fact that molten metals are electrically conducting opens up possibilities to apply the magnetic fields to control the behavior of the melts during solidification and, therefore, to improve product quality. During metal solidification, magnetic fields have been applied to shape the solidifying melts (i.e., electromagnetic molding), stir the melts at desired locations (i.e., electromagnetic stirring), and reduce the melt disturbance or flow irregularities or turbulence (i.e., electromagnetic braking). The use of the fields has resulted in benefits of improved internal metallurgical structure, reduced inclusions and liquidation, improved uniformity of compositions and mechanical properties, and alleviation of operation constraints.
Invented in the late 1960s,21 electromagnetic casting or electromagnetic mold is now one of the widely used technologies for ingot production in the metals industry, particularly the aluminum industry. In this process, a water-cooled mechanical mold used in conventional direct chill (D.C.) casting processes is replaced by a configured magnetic pressure field that is generated by a water-cooled alternating current (a.c.) induction coil surrounding the solidifying melt. Figure 2 illustrates the basic design of an electromagnetic caster for the production of aluminum ingots of rectangular cross section.
 |
| Figure 2. A schematic of electromagnetic casting processes used for the production of aluminum ingots.27 |
The operating principle of electromagnetic casting is now well understood. An a.c. current flows through the inductor and generates an eddy current in the melt. The eddy current interacts with the imposed and self-induced magnetic fields to produce the Lorentz force in the melts (Equation 3), which may be decomposed into a potential component and a vortical component.15,22,23 The former is responsible for melt support and free-surface deformation by balancing the metostatic pressure of the melt column undergoing solidification, while the latter creates stirring in the melt near a free surface adjacent to the inductor.
The use of an electromagnetic mold eliminates or alleviates many mold-related problems associated with D.C. casting, resulting in ingots with better surface quality.24 While melt support is the intent of the original design, melt agitation in the near-surface region is an inevitable by-product, which can be viewed in two ways. In some respects, stirring may result in the benefit of local-alloy-element homogenization. In other respects, it may also be a culprit for trapping oxides floating on the surface into the final products. The stirring and melt-support phenomena have been studied extensively in literature.15,23,25-27 Electromagnetic molds have been used in the production of aluminum ingots of various cross sections and are being explored for the casting of other metals.17,28 The idea of electromagnetic molding has also been explored to control the meniscus deformation of the solidifying melts during the initial stage of ingot solidification29 and in thin-strip casting.28 A recent review by Evans30 provides a detailed discussion on the basic features of the electromagnetic casting for metals as well as recent progress in applications.
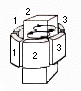
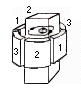
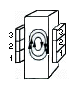
STIRRING MOTION (3 phase) 1 2 2 3 3 |
|---|
| Rotary Stirring |
Linear Stirring |
 |
 |
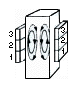 |
 |
| Symmetric |
Opposed |
Symmetric |
Opposed |
| Figure 3. The designs of linear and rotary electromagnetic stirring systems used during metal casting along with associated flow patterns. For both linear and rotary stirring, single- or double-flow loops are possible, depending on the magnetic fields applied. |
The use of electromagnetic stirring during metals solidification dates back to the 1930s,4,5 and a comprehensive review of the stirring activities up to the early 1980s was provided by Tzavaras and Brody.31 Like electromagnetic casting, electromagnetic stirring is produced by the Lorentz force generated by an a.c. inductor (Equation 3). Unlike electromagnetic casting where stirring occurs near the surface region, however, electromagnetic stirrers are designed to deliberately produce melt convection deep in the liquid pool near the solidification front. Thus, lower-frequency magnetic fields are used to allow the Lorentz force to penetrate deeply into the molten-metal pool.
Two types of electromagnetic stirrers are commonly used in practice: the linear stirrer and rotary stirrer. A linear stirrer operates basically the same way as an induction furnace. The design entails the placement of a stack of coils around the casting metal to generate a primary motion that recirculates along the casting direction. A rotary stirrer is basically an electric motor. It uses a rotating magnetic field to produce a swirling flow in the liquid pool. Figure 3 contrasts the linear and rotary stirring modes and the primary fluid motions in the liquids. The two modes may be applied either individually or in a combined fashion and stirring may be employed in various stages of solidification processes6,31 (i.e., in mold, below mold, and at the final stage of solidification).
 |
| Figure 4. The basic mechanism of grain multiplication or grain refinement resulting from strong stirring in the solidification region. The stirring generates shear to break the dendrite tips and circulates the debris in the liquid pool. |
Perhaps one of the major motivations for applying electromagnetic stirring during solidification processing comes from the understanding that a strong melt flow will generate strong shear stresses, and the shear stresses will shed away the newly formed dendrites near the solidification front.32-37 The newly formed dendrite debris is then transported into the bulk liquid pool of higher temperature by convection. Some of the dendrites are remelted and disappear while others survive and are transported back to the solidifying region. These surviving broken dendrites then form additional nucleation sites upon which further grain growth will occur, thereby resulting in grain refinement in the final casting products.6,7,31-37 This basic grain multiplication mechanism induced by strong electromagnetic stirring is depicted in Figure 4.
Aside from refining internal structures, electromagnetic stirring also has the advantages of homogenizing alloy elements, reducing porosity and segregation, and minimizing internal cracks. Table I summarizes the benefits of electromagnetic stirring when applied in the mold region (mold electromagnetic stirrer), below the mold or strand (strand electromagnetic stirrer), and in the final stage of solidification (final electromagnetic stirrer).
| Table I. The Effects of Electromagnetic Braking and Stirring during the Continuous Casting of Metals |
|---|
| Electromagnetic Brake |
Mold Electromagnetic Stirrer |
Strand Electromagnetic Stirrer |
Final Electromagnetic Stirrer |
| Mold Powder Entrapments |
— |
— |
— |
| Surface Cracks |
Surface Slags |
— |
— |
| Break-Outs |
Break-Outs |
— |
— |
| Subsurface Inclusions |
Subsurface Inclusions |
— |
— |
| Inner Inclusions |
Pinholes |
— |
— |
| Macrosegregation |
Blowholes |
— |
— |
| Prolonged Mold Life |
Columnar Structure |
Columnar Structure |
V-Segregation |
| — |
Internal Cracks |
Internal Cracks |
— |
| — |
Center-Line Segregation |
Center-Line Segregation |
Center-Line Segregation |
| — |
Center Porosity |
Center Porosity |
Center Porosity |
Electromagnetic brake uses the principle of magnetic damping to reduce the turbulence flow and unwanted flow instability in the solidifying melt pool. Magnetic damping (Figure 1b) originates from the direct interaction of the applied direct current (d.c.) magnetic field and the melt velocity. In normal continuous casting operations, liquid metals are delivered through the downspout nozzle into the liquid pool and are cooled and solidified when passing through the water-cooled mold.38 The liquid-metal jet leaving the nozzle penetrates into the surface region, carrying with it nonmetallic inclusions and gas bubbles, which are the origins of the surface and internal defects.39 The application of a d.c. magnetic field near the nozzle-exit region produces damping effects and reduces the turbulent-flow velocity associated with the melt jets leaving the nozzle.
Figure 5 shows a typical design of magnetic damping in controlling the liquid jets from the delivering nozzle. This reduction in velocity helps to slow down the penetration of the inclusions-laden liquid metals into the surface region and the deep slump below the nozzle, thereby allowing the inclusions and gas bubbles to float up to the melt meniscus more quickly.40 Electromagnetic braking also helps to reduce macrosegregation by reducing the chance of bringing broken dendrites that are rich in alloy elements into the melting pool and then settling in the center of the ingot, which is a quality issue of more concern to aluminum producers.40 Table I also lists the advantages of electromagnetic braking as applied to continuous casting of metals.
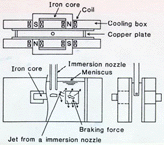 |
| Figure 5. A typical design of the magnetic-field configuration used for damping the turbulence of the melt jets leaving the downspout nozzle.39 |
Single crystals for electronic applications are solidified or grown from semiconductor melts. While many different techniques have been developed, the Czochralski and the floating zone (crucibleless) methods are perhaps the two most popular ones.41,42 In the electronics industry, the majority of commercial crystals are grown using the Czochralski method, while the floating zone method is primarily used for the growth of single crystals of extra-high purity demanded for rectifier and infrared sensor and detector applications.
Semiconductor crystal growth and metal casting both involve solidifying liquid into solid and share similarities in process-design concepts; however, the quality demand for single crystals differs greatly from that for metals; thus, the details of solidification-processing operation and required thermal and flow management are quite different. In contrast with metal castings, whose structures consist of numerous grains oriented randomly, a single crystal is a single grain in which atoms are arranged in perfect orientation. The impurities in semiconductor crystals include dislocations and foreign atoms resulting from doping or oxygen from crucible walls and are tightly controlled at a certain level (i.e., 0.01-10 ppm or 1015 ~ 1018 atoms/cm3), depending on specific applications. For high-yield production of microchips required by integrated circuit designers, it is essential that there is a radially as well as microscopically uniform distribution of these impurities when present. This requires that the temperature gradient be carefully controlled at the crystal-melt interface so that liquid atoms are given sufficient time to incorporate into equilibrium-lattice positions of the crystal. Thus, semiconductor crystals are small in size (10 ~ 15 cm in diameter) and growth rate is slow (a few centimeters per hour) in comparison with metal ingots.
A semiconductor is basically an electrical insulator at room temperature. However, it becomes a good electrical conductor when in a molten stage. This property permits the use of the electromagnetic fields to achieve a thermal and flow environment favorable for growing crystals of better quality. As in metal solidification, the fields are used for the purposes of melt support (or electromagnetic crucible), stirring, and damping during crystal growth. However, the details of operation, such as field configurations and process-control parameters, are different from metal solidification and are tailored to satisfy the more restricted processing and quality requirements imposed by the semiconductor industry.
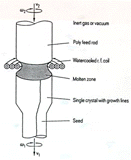 |
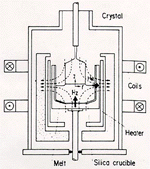
| Figure 6. A schematic of floating-zone processes used for silicon single-crystal growth.42 The process is very similar in concept to electromagnetic casting. |
The floating zone (crucibleless) process or electromagnetic crucible is a technique to grow single crystals of low dislocation and high purity for high-power device applications. Invented in 1928, the process currently produces 15% of crystals consumed by the electronics industry.42,43 The process is schematically illustrated in Figure 6. In principle, the process is very similar to electromagnetic casting; the major difference is that the melt is produced by the induction melting of the feeding polycrystals, which results from the interaction of the eddy currents or the joule heating generated in the polycrystals by the surrounding inductor.43-49 The inductor also generates the electromagnetic force, which supports the melt zone against gravity and drives a melt-recirculating flow near the free surface.43,45 The applied frequency is in the MHz range, which compares with KHz used in electromagnetic casting.
During the operation, a necking melt shape is maintained, and polycrystals and single crystals may rotate to provide better mixing. Superimposed on the forced electromagnetic flow near the surface and mechanical rotation are strong buoyancy- and surface-tension-driven flows. The whole process is conducted in a vacuum and requires very delicate control to minimize the thermal fluctuations and flow instabilities associated with buoyancy and thermocapillary flows. Because of the fact that the semiconductor melt is not in contact with any physical crucible, single crystals of very low oxygen content and extra-high purity can be obtained with this process. Although mainly employed for producing semiconductor crystals, it has also been used for the solidification processing of other types of materials.50
In the melt pool from which a single crystal is grown, thermal gradients are present and cause strong buoyancy-driven convection and surface-tension-driven flows where there is a free surface. It is now understood that the melt-convective flows are at least partially turbulent, which is largely responsible for crystal imperfections and a radially and microscopically nonuniform distribution of dopant concentration and impurities in the crystals. One of the recently explored ideas to reduce the detrimental effect of convection turbulence is to apply electromagnetic stirring to induce a forced flow that overpowers the convective flows responsible for the melt turbulence.51-54 The idea is motivated by the success of electromagnetic stirring in the metal industry and by the recognition established through years of study that although turbulence is unwanted, steady-state convection lies at the heart of the production of uniform single crystals.8 In contrast with the metals industry, where different modes of stirring are applied, only rotary electromagnetic stirring has been applied in single-crystal growth processes.51,52
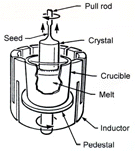 |
| Figure 7. A schematic of rotary electromagnetic stirring used for Czochralski growth of semiconductor single crystals. |
Figure 7 shows a possible coil-design arrangement for rotary electromagnetic stirring during crystal growth. Recent studies showed that adequate electromagnetic rotation indeed helps to grow crystals with a better radial and microscopic uniformity.51 This effect may be explained by the fact that deliberate stirring by electromagnetic forces helps to smear out the flow irregularities and produce a desired flow pattern for melt mixing near the crystal-liquid interface, leading to a reduction of solutal striation in crystals. Electromagnetic stirring may also be applied in combination with mechanical rotation of the crucibles and/or crystals for a better flexibility in thermal and flow management.
It is important to note that there is a major difference between metal and semiconductor stirring, although stirring is preferred at the solid-liquid interface for both cases. Metal stirring is intended to produce a fine-grain structure; hence, high shear turbulence flow is desirable and necessary to break up the dendrites. During crystal growth, on the other hand, an adequate Lorentz force is needed to smear out thermally induced flow instabilities and mix the melt near the solidification front, but not mix so strong as to cause forced-flow turbulence. Also, unlike metal casting, where stirring is a well-established technology, electromagnetic stirring during crystal growth is not yet matured and is an active research subject being vigorously pursued by single-crystal growers.
 |
| (a) |
 |
| (b) |
 |
| (c) |
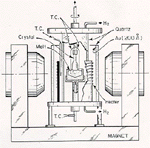
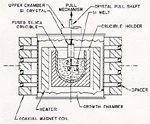
| Figure 8. Czochralski growth of semiconductor single crystals in various d.c. magnetic fields: (a) transverse magnetic-field configuration,56 (b) axial magnetic-field configuration,57 and (c) cusped magnetic-field configuration.62
|
While stirring is studied as an alternative to control melt turbulence, a more popular and well-established technology has been to apply a d.c. magnetic field to damp out turbulence and flow irregularities to reduce the solutal striation and other defects in the final crystals.8,55-62 The effect of the magnetic field on the improvement of single-crystal qualities grown from melt was first demonstrated in the 1960s,55 and magnetic damping is now widely practiced in the semiconductor industry.8 In crystal-growth practice, the strength of an applied magnetic field ranges from 0.05-3 Tesla. With high-temperature superconducting magnets available, higher field strengths would also be possible.
Many different magnetic-field configurations have been applied to achieve an adequate damping effect on convection in the melt pool.8 This is in contrast with the metals industry, which has considered mainly transverse magnetic fields for the purpose of braking turbulent jets leaving the downspout nozzle. Earlier applications used transverse magnetic fields, by which two magnetic poles are placed in opposition to generate a magnetic field perpendicular to the crystal-growth direction.56 The axial magnetic field, which is parallel to the growth direction, was later considered.57 In both cases, magnetic-field distribution is uniform. Recently, efforts have been directed to apply the cusped magnetic fields generated by a pair of Helmholtz coils placed coaxially above and below the crystal-melt interface and operated in an opposed current mode.60,62
Figure 8 compares the transverse, axial, and cusp field configurations used in Czochralski single-crystal growth furnaces. The cusped magnetic field is nonuniform such that it has sufficient strength in the bulk melt, is approximately normal to the crucible-melt interface, and yet has no axial component at the crystal-melt interface. Compared with axial and transverse magnetic fields, the cusped configuration gives rise to a more favorable environment—adequately damped bulk convection in the melt, a thickened boundary layer near the crucible-melt interface, and a well-mixed flow near the crystal-melt interface.59,61 Crystals grown under this configured magnetic field have lower oxygen contents and more radial uniformity.62 A comprehensive review of the history and application of magnetic damping during single-crystal growth was given in a recent paper by Series and Hurle.8
For electrically conducting fluids, magnetic fields can be used to support the melts in place of a mechanical container, provide an environmentally friendly yet effective means for melt stirring, and reduce unwanted turbulent flows and fluctuations associated with melt convection. These remarkable effects of magnetic fields on solidifying melts have led to the development of various magnetically assisted solidification technologies for producing metal ingots and semiconductor crystals of superb quality.
The electromagnetic mold or crucible is based on the concept of magnetic support and replaces a mechanical mold or crucible by the Lorentz forces generated by an inductor surrounding the solidifying melt. Support or shape of the melt eliminates the possible contamination of impurities originated from the container. As such, it has become the method of choice for the production of high-purity and low-defect solidification products, whether they are metal-casting ingots or semiconductor single crystals.
Electromagnetic stirring results from a deliberate application of a.c. magnetic fields and allows the melt convection to be generated at locations where most needed. It is applied in the mold region, below-mold region, and in the final stage of solidification during the continuous casting of metals. Both linear and rotary stirring has been applied in the metals industry; rotary stirring has been the only mode used in the semiconductor industry. While electromagnetic stirring in metals has enjoyed a long history, it has just started in the single-crystal growth community.
Electromagnetic brake or magnetic damping uses the interaction of the melt convection and a d.c. magnetic field to produce an opposing force to the flow motion in the solidifying melt. It has been widely used in both the metal and semiconductor industries to suppress the melt turbulence and flow instabilities. In the metals industry, mainly transverse magnetic fields have been considered with the purpose of slowing down or braking the turbulence of liquid jets issued from the downspout nozzle. In contrast, many different magnetic-field configurations have been explored in the semiconductor industry to damp out the turbulence and flow instabilities or fluctuations associated with melt convection.
The application of magnetic fields has now become widely practiced in the materials industry for the solidification processing of metals and semiconductors and has resulted in improved quality and process control. Ever-increasing global economic competition has created a black-hole type of demand for better quality, which in turn generates a powerful thrust for improved process design and operation. Because of different development histories and different quality requirements, metal and semiconductor researchers have different focuses in their research on solidification processing in magnetic fields, though the design principles applied are the same. Metals researchers, while perfecting the current practice, are now exploring the possibility of extending the use of the electromagnetic fields in near-net-shape casting, thin-gauge casting, and other novel casting processes. On the other hand, crystal growers are preoccupied with adapting electromagnetic stirring in semiconductor melts while developing more effective magnetic damping field configurations.
The author gratefully acknowledges the financial support provided by NASA (NCC8-92, NCC3-435) and the National Science Foundation (Grant No. NSF/CTS-9622275) and helpful discussions with H.C. de Groh at NASA Lewis Research Center.
1. M. Fleming, Solidification Processing (New York: McGraw-Hill, 1974).
2. W.A. Tiller, The Science of Crystallization (Cambridge, U.K.: Cambridge University Press, 1991).
3. W. Kurz and D.J. Fisher, Fundamentals of Solidification, 3rd ed. (Switzerland: Trans Tech Publications, 1989).
4. D.A. Shtanko, "Solidification of Steel in a Magnetic Field," Zh. Tekh Fiz., 3 (6) (1933), p. 1085.
5. A. Bruchanov, "Solidification of Steel in a Rotating Magnetic Field," Stahl Eisen, 54 (1934), p. 1111.
6. E. Takeuchi et al., "Applied MHD in the Process of Continuous Casting," Magnetohydrodynamics in Process Metallurgy, ed. J. Szekely et al. (Warrendale, PA: TMS, 1992), pp. 189-202.
7. S. Asai, Metallurgical Aspects of Electromagnetic Processing of Materials in Liquid Metal Magnetohydrodynamics, ed. J. Lielpeteris and R. Moreau (Boston, MA: Kluwer Academic Publishers, 1989).
8. R.W. Series and D.T.J. Hurle, "The Use of Magnetic Fields in Semiconductor Crystal Growth," J. Crystal Growth, 113 (1991), pp. 305-328.
9. J.D. Jackson, Classical Electrodynamics (New York: John Wiley & Sons, 1975).
10. W.F. Hughes and F.J. Young, The Electromagnetohydrodynamics of Fluids (New York: John Wiley & Sons, 1966).
11. R.E. Holmes and A.J. Chapman, "Condensation of Freon-114 in the Presence of a Strong, Non-Uniform, Alternating Electric Field," J. Heat Transfer, 92 (1970), pp. 616-620.
12. T.B. Jones, "An Electrohydrodynamic Heat Pipe," Int. J. Heat Mass Transfer, 16 (1973), pp. 1045-1048.
13. B. Tillotson and J. Houston, "Diamagnetic Manipulation for Microgravity Processing" (paper presented at the 35th Aerospace Science Meeting, Reno, NV: January 1997).
14. H.K. Moffat, "Electromagnetic Stirring," J. Phys. Fluids, 3 (5) (1991), pp. 1336-1343.
15. B.Q. Li, J.W. Evans, and D.P. Cook, "An Improved Mathematical Model for Electromagnetic Casters and Testing by a Physical Model," Mat. and Met. Trans. B, 22B (1991), pp. 121-134.
16. B.Q. Li, "The Fluid Flow Aspects of Electromagnetic Levitation Processes," Int. J. Eng. Sci., 32 (1) (1994), pp. 45-67.
17. B.Q. Li, "A Finite Element Analysis of Magnetically-Driven Recirculating Flow in Electromagnetic Near Net Shape Casting," J. of Mat. Processing Technology, 3 (1995), pp. 351-359.
18. G.M. Opeper and J. Szekely, "The Effect of an Externally Imposed Magnetic Field on Buoyancy Driven Flow in a Rectangular Cavity," J. Crystal Growth, 64 (1983), pp. 505-515.
19. J.A. Shercliff, A Textbook of Magnetohydrodynamics (New York: Pergamon, 1965).
20. B.Q. Li, Magnetic Damping of Convection during Unidirectional Solidification, report submitted to NASA, Lewis (1997).
21. Z.N. Getslev, "Casting in an Electromagnetic Field," J. Metals, 23 (10) (1971), pp. 38-39.
22. R. Ricou and C. Vives, "Experimental Study of Electromagnetic Casting of Aluminum Alloys," Mat. and Met. Trans. B, 16B (1985), pp. 377-384.
23. J. Sakane, B.Q. Li, and J.W. Evans, "Mathematical Modeling of Meniscus Profile and Melt Flow in Electromagnetic Casters," Mat. and Met. Trans. B, 19 (1988), pp. 397-408.
24. E.M. Dunn, Metallurgical Structure of Electromagnetically Cast Extrusion Billet Light Metals, ed. W.S. Peterson (Warrendale, PA: TMS, 1979), pp. 671-782.
25. Z.N. Getselev et al., "Calculation of the Parameters of Electromagnetic Crystallizers for the Casting of Round Ingots," Magnit. Girodyn., 2 (1975), pp. 144-148.
26. D.P. Cook and J.W. Evans, "A Three-Dimensional Mathematical Model of Electromagnetic Casting and Testing Against a Physical Model," Mat. and Met. Trans. B, 26B (1995), pp. 1263-1279.
27. J. Rappaz and R. Touzani, "Numerical Simulation of Solidification Processes in Electromagnetic Casting," in Ref. 6, pp. 181-189.
28. D.P. Cook, J.W. Evans, and J. Grandfield, "Application of a Mathematical Model to Thin Strip Electromagnetic Casting," in Ref. 6, pp. 145-150.
29. M. Nakada, K. Mori, and T. Osaka, "Control of Initial Solidification in Continuous Casting Mold," in Ref. 6, pp. 203-207.
30. J.W. Evans, "The Use of Electromagnetic Casting for Al Alloys and Other Materials," JOM, 47 (5) (1995), pp. 38-41.
31. A.A. Tzavaras and H.D. Brody, "Electromagnetic Stirring and Continuous Casting—Achievements, Problems and Goals," J. Metals, 36 (3) (1984), pp. 31-37.
32. R.T. Gass and T.T. Jackson, "Use of Electromagnetic Stirring During Slab Casting for Hot Rolled Tubular Products," 1991 Steelmaking Conference Proceedings (Pittsburgh, PA: AISI, 1991), pp. 539-545.
33. F.C. Langenberg et al., "Grain Refinement by Solidification in a Moving Electromagnetic Field," J. Metals, 13 (12) (1961), pp. 895-899.
34. P.G. Schmidt, "The Effect of Mechanical Stirring of Molten Steel on the Solidification of a Continuously Cast Product," Steel USSR, 7 (4) (1977), pp. 216-217.
35. R. Perie and J.C. Ruth, "Stirring Steel in the Mould," Iron Steelmaker, 4 (2) (1977), pp. 24-29.
36. R. Widdowson and H.S. Marr, "Metallurgical Aspects of Electromagnetic Stirring During the Solidification of Low Carbon Steels," Sheffield International Conference on Solidification and Casting 1977, Metals Society Book 192 (Metals Society, London: 1979), pp. 547-552.
37. C. Vives, "Hydrodynamic, Thermal and Crystallographic Effects of an Electromagnetically Driven Rotating Flow in Solidifying Aluminum Melts," Int. J. Heat Mass Transfer, 33 (12) (1990), p. 2585.
38. B.Q. Li, "Production of Thin Strips by Twin Roll Casting," JOM, 47 (5) (1995), pp. 29-33.
39. H. Tozawa and S. Takeuchi, "Flow Control of Molten Steel in Continuous Casting Mold by Static Magnetic Field," in Ref. 6, pp. 215-222.
40. C. Vives, "Effects of Magnetically Damped Convection During the Controlled Solidification of Metals and Alloys," Int. J. Heat Mass Transfer, 33 (1987) p. 479.
41. S. Wolf and R.N. Tauber, "1986: Silicon Processing for the VLSI Era," Process Technology, 1 (Sunset Beach, CA: Lattice Press, 1986).
42. W. Keller and A. Muhlbauer, Floating-Zone Silicon (New York: Marcel Dekker, 1981).
43. A. Muhlbauer and F.M. Kamel, "Artificial Growth of Large Silicon Single Crystals by the Floating Zone Method," Elektrowqaerme Internation, 47 (6) (1989), pp. 529-545.
44. H. Riemann et al., "Silicon Floating Zone Process: Numerical Modeling of RF Field, Heat Transfer, Thermal Stress and Experimental Proff For 4 Inch Crystals," J. Electrochem. Soc., 142 (3) (1995), pp. 1007-1014.
45. S. Song and B.Q. Li, "Modeling of Melt Flow and Free Surface Deformation in Zone Refining Processes with RF Induction," Application of Modeling and Sensors in Materials Processing (Warendale, PA: TMS, 1997).
46. A. Muhlbauer, W. Erdmann, and W. Keller, "Electrodynamic Convection in Silicon Floating Zones," J. Crystal Growth, 64 (1983), pp. 529-545.
47. J.Y. Murphy, "A Numerical Simulation of Flow, Heat and Mass Transfer in A Floating Zone at High Rotational Reynolds Numbers," J. Crystal Growth, 83 (1987), pp. 23-34.
48. E.D. Lyumkis and E.N. Martuzane, "The Effect of Electromagnetic Forces on the Hydrodynamics of a Melt in the Process of High Frequency Floating Zone Melting," Magnetohydrodynamics, 3 (1983), pp. 95-102.
49. E.D. Lyumkis, B.I. Martuzane, and E.N. Martuzane, "Effect of Thermocapillary Convection and MHD Flow on Impurity Distribution in Zone Melting," Hydrodynamics and Heat and Mass Transfer in Materials Production, Izdatel'stvo Nauka (1990), pp. 124-130.
50. S. Otani, T. Tanaka, and Y. Ishizawa, "Effect of PrB Addition on Lab Crystals Grown by the Floating Zone Method," J. Crystal Growth, 113 (1991), pp. 329-332.
51. M. Salk et al., "CdTe and CdTeSe Crystals Grown by the Travelling Heater Using a Rotating Magnetic Field," J. Crystal Growth, 138 (1994), pp. 161-167.
52. D.C. Gillies et al., "Solidification of II-VI Compounds in a Rotating Magnetic Field," NASA Microgravity Materials Conference, ed. F. Szofran et al. (Huntsville, AL: NASA, 1996), pp. 241-242.
53. H. Wiemann et al., "3D-Modeling of Marangoni-Convection in Floating Zone Growth of GaAs Under Microgravity and Rotating Magnetic Fields" (paper presented at the Joint Xth European and Vith Russian Symposium on Physical Sciences in Microgravity, St. Petersburg, Russia, June 1997).
54. A.S. Senchenkov et al., "MCT Crystal Growth From Solution Within a Rotating Magnetic Field" (paper presented at the Joint Xth European and Vith Russian Symposium on Physical Sciences in Microgravity, St. Petersburg, Russia, June 1997).
55. H.P. Utech and M.C. Fleming, "Elimination of Solute Banding in Induium Antimonide Crystals by Growth in a Magnetic Field," J. App. Phys., 37 (2) (1966), pp. 2021-2024.
56. A.F. Witt, C.J. Herman, and H.C. Gatos, "Czochralski-Type Crystal Growth in Transverse Magnetic Fields," J. Mat. Sci., 5 (1970), pp. 822-824.
57. K.M. Kim and P. Smetana, "Striations in CZ Silicon Crystals Grown Under Various Axial Magnetic Field Strengths," J. App. Phys., 58 (7) (1985), pp. 2731-2734.
58. K. Tarashima, A. Yahata, and T. Fukuda, "Growth Condition Dependence of EL2 Concentrations in Magnetic Field Applied Liquid-Encapsulated Czochralski GaAa Crystals," J. App. Phys., 59 (3) (1985), pp. 982-984.
59. M. Mihelcic and K. Wingerath, "Numerical Simulations of the Czochralski Bulk Flow in an Axial Magnetic Field," J. Crystal Growth, 71 (1985), pp. 163-168.
60. R.W. Series, "Effects of a Shaped Magnetic Field on Czochralski Silicon Growth," J. Crystal Growth, 97 (1989), pp. 92-98.
61. T. Kimura et al., "The Effect of Strong Magnetic Field on Homogeneity in LEC GaAs Single Crystal," J. Crystal Growth, 79 (1986), pp. 264-276.
62. H. Hirata and K. Hoshikawa, "Silicon Crystal Growth in a Cusp Magnetic Field," J. Crystal Growth, 96 (1989), pp. 745-755.
ABOUT THE AUTHOR
B.Q. Li earned his Ph.D. in engineering from the University of California at Berkeley. He is an associate professor of mechanical engineering at Washington State University. Dr. Li is also a member of TMS.
For more information, contact B.Q. Li, Washington State University, School of Mechanical and Materials Engineering, P.O. Box 642920, Pullman, Washington 99164; (509) 335-7386; fax (509) 335-4662; e-mail li@mme.wsu.edu.
Copyright held by The Minerals, Metals & Materials Society, 1998
Direct questions about this or any other JOM page to jom@tms.org.




 (SI unit) for a macroscopic homogeneous medium9
(SI unit) for a macroscopic homogeneous medium9
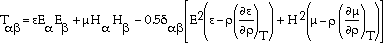
 is the electric permittivity, E
is the electric permittivity, E is the
is the  th component of the electric field, µ is the magnetic permeability, H
th component of the electric field, µ is the magnetic permeability, H is the
is the  th component of the magnetic field,
th component of the magnetic field,  is the density of the fluid, and T is the temperature. The Kroneker delta
is the density of the fluid, and T is the temperature. The Kroneker delta 

 takes the value
takes the value 

 = 1 if
= 1 if  =
=  and
and 

 = 0 if
= 0 if 

 , where
, where  ,
,  = 1, 2, 3.
= 1, 2, 3.
 (
( µ/
µ/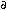
 )T
)T  0].9 Therefore, convection in the melt pool is influenced by the volumetric momentum source of the electromagnetic origin, the Lorentz force. The Lorentz force F is equal to the divergence of the Maxwell stress tensor
0].9 Therefore, convection in the melt pool is influenced by the volumetric momentum source of the electromagnetic origin, the Lorentz force. The Lorentz force F is equal to the divergence of the Maxwell stress tensor 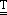 , viz.,
, viz.,
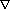 ·
· 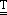

 ,
, denotes the derivative of T
denotes the derivative of T
 with respect to
with respect to  .
.
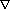 x H x B =
x H x B =  (E + u x B) x B
(E + u x B) x B is the electric conductivity. Also, to arrive at Equation 3, use has been made of Ohm's law for a moving conducting fluid
is the electric conductivity. Also, to arrive at Equation 3, use has been made of Ohm's law for a moving conducting fluid
 (E + u x B)
(E + u x B) E x B
E x B u x B x B
u x B x B





