 |
51 (2) (1999), pp. 21-27. |
|---|
 |
51 (2) (1999), pp. 21-27. |
|---|
 |
| TABLE OF CONTENTS |
|---|
Since icebergs were first proposed as potential aircraft carriers in World War II, research has led to a better understanding of the mechanical behavior of ice. While work remains, especially in relating fracture on the small scale to that on the larger scale and to the appropriate structural features, the groundwork in materials science has been laid. This paper presents an overview of the structure and mechanical behavior of polycrystalline terrestrial ice.
Since then ice research has flourished. Nucleation and growth from both vapor and liquid states has been studied and placed within the context of classical thermodynamics and kinetics. The structure of ice and natural ice formations has been examined and then related to the thermal-mechanical history of the material. Electrical properties have been measured and explained in terms of the number density and mobility of protonic charge carriers. Optical and thermal behaviors have been explored. Mechanical behavior has been thoroughly studied, from the flow and fracture of single crystals to the creep of glaciers and the fracturing of Arctic sea-ice covers. Indeed, over the past ten years alone more than 10,000 papers on ice have appeared in the scientific and engineering literature.
Why the interest? Ice, it turns out, is a factor in activities as diverse as skiing and skating, rainmaking, polar marine transportation, and cold ocean oil exploration. It is an element in the degradation of cold concrete and other porous materials. It forms as "icing" on airplanes and electrical transmission lines. Ice is also a factor in global climate, evident perhaps from the facts that the Antarctic and Greenland ice sheets cover about 10% of the earth's land area and sea ice covers about 10% of the ocean surface either seasonally or perennially. In addition, the ice sheets and the air bubbles entrapped therein are the storehouses of the pa-leoclimate record. Ice is also a major constituent of the moons of Jupiter and of other extraterrestrial bodies.
This article reviews the structure and mechanical behavior of polycrystalline terrestrial ice. Fuller accounts are given in the literature cited and in the following references: ice physics by Hobbs2 and by Petrenko and Whitworth;3 ice-structure interactions by Sanderson;4 sea ice by Weeks;5 ice mechanics by Michel;6 and plastic flow and fracture in the Johannes Weertman Symposium.7 Curtin8 offers a historical perspective through the eyes of the U.S. Navy, and Levi9 describes the role of ice in the global heat budget. Durham et al.10 discuss the creep of planetary ice.
 -130°C). Amorphous ice can be obtained by depositing vapor at still lower temperatures and by compressing ice Ih at liquid nitrogen temperature. In addition to the elemental phases are clathrate hydrates. These are crystalline compounds composed of a large H2O cage in which Xe, Ar, or CH4, for instance, is entrapped. Clathrates are of economic interest because they offer an abundant source of natural gas.
-130°C). Amorphous ice can be obtained by depositing vapor at still lower temperatures and by compressing ice Ih at liquid nitrogen temperature. In addition to the elemental phases are clathrate hydrates. These are crystalline compounds composed of a large H2O cage in which Xe, Ar, or CH4, for instance, is entrapped. Clathrates are of economic interest because they offer an abundant source of natural gas.
The relationship to Ic lies in a common tetrahedral arrangement of H2O molecules. Ic, however, has the diamond cubic crystal structure, in which the stacking sequence relative to the {111} plane is . . . AABBCCAABBCC . . . ; its lattice parameter (at -130°C) is 0.635 nm.
The hydrogen atoms are arranged randomly11 according to the Bernal-Fowler rules.12 First, two protons must be located near each oxygen. Second, only one proton must lie on each O-O bond. The random arrangement persists at low temperatures, owing to the extraordinarily slow reorientation of the H2O molecule (greater than 100 years at liquid nitrogen temperature), and this leads to a large amount (3.41 J/mol.) of zero-point entropy. Ice does not violate the third law of thermodynamics.
Point Defects
 |
| Figure 2: A composite x-ray topograph showing slip bands in two adjacent grains of an ice Ih polycrystal slowly strained under uniaxial compression at -6°C. The bands formed during in-situ straining through slip on basal planes. The images of each grain were obtained from separate Laue spots (the diffraction vectors are indicated), and, hence, an image of the grain boundary is present in both. The dislocations in the slip bands were nucleated at facets on the grain boundaries, such as those arrowed, and then traversed the grains to relieve the stresses associated with grain-boundary sliding. During straining, the dislocations in the slip band starting at S were observed to traverse the grain and pile up at the opposite boundary at P. (From Liu, Baker, and Dudley.16) |
Violations of the Bernal-Fowler rules create ionic and Bjerrum defects.15 If the proton moves along the O-O bond, then the first rule is violated: one proton near an oxygen atom creates an OH- ion; three create an H3O+ ion. If the proton moves around the oxygen atom, then the second rule is violatedno hydrogen atom on an O-O bond creates L-type Bjerrum defects (L stands for leer, which means empty in German); two protons create a D-type Bjerrum defect (D means doublet). Both kinds of defects contribute to electrical conductivity (the migration of ions allows protons to move from one end of a bond to the other), and the movement of Bjerrum defects allows protons to move from one side of an oxygen atom to another. Without the migration of both defects, long-range protonic conduction could not occur.
Despite the fact that water is a universal solvent, the solubility of substances in ice Ih is very low. The solubility of HCl, for instance, is 3 X 10-6 at -10°C. Exceptions are HF and NH3. These molecules are assumed to dissolve substitutionally, creating L-defects in HF and D-defects in NH3, as well as additional ionic defects. The impurities increase electrical conductivity.
Dislocations
Figure 2 shows a composite x-ray topograph illustrating slip bands in two adjacent grains in a polycrystal. In both crystals slip occurred by dislocation glide on basal or {0001} planes.16 The Burgers' vectors were parallel to the direction 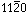 >
>
A unique feature is worth noting. Because the protons in ice Ih are arranged randomly, the translation of part of the crystal relative to the rest by the Burgers' vector will not exactly reproduce the atomic arrangement.18 Instead, the translation introduces Bjerrum defects. The stress needed to create them (of formation energy 0.68 eV) is orders of magnitude greater than can be accounted for by the actual flow stress.18 This implies that some kind of protonic rearrangement must occur. However, the precise way in which dislocations overcome the obstacle presented by proton disorder is not yet known.
Planar Defects
Stacking faults have been observed in as-grown crystals using x-ray topography.19 They can be eliminated by annealing and so are considered to be unstable defects. Twins have not been observed, in material either well annealed or plastically deformed. Barring free surfaces, grain boundaries are the most prominent planar defect. They exhibit ledges, some as large as 1 mm (Figure 2), and close to the melting point they contain liquid water in submillimeter-sized veins that lie along lines of intersection.20 Within warm sea ice they also contain millimeter-sized brine pockets. Grain boundaries are sites of sliding and crack nucleation and are thus important microstructural features.
Arctic sea ice5 forms directly upon the unidirectional solidification of salt water. Floating covers form and consist primarily of columnar-shaped grains elongated in the growth direction, reminiscent of metallic ingots. Once thickened to a few centimeters, the covers develop a strong growth texture in which the crystallographic c-axes are confined more or less to the horizontal plane, but are either randomly oriented within this plane or aligned22 with the ocean current. Sea ice is characterized also by an intragranular porous substructure that consists of submillimeter diameter air bubbles and brine pockets, totaling 4-5 vol.%, arrayed in a plate-like manner parallel to basal planes. Also, cold sea ice may contain precipitates of sea salts (mainly NaCl). Both deformation and growth textures lead to macroscopically anisotropic inelastic behavior.
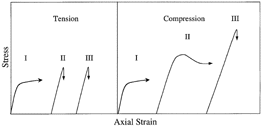 |
| Figure 3: Schematic stress-strain curves. I, II, and III denote low-, intermediate-, and high-strain rates. The arrows indicate either ductile (horizontal) or brittle (vertical) behavior. |
Inelastic behavior is markedly anisotropic. The critical resolved shear stress for non-basal slip is 60 times or more greater than that for basal slip,24 and this presents a problem for polycrystals. Basal slip allows only two independent deformation modes. When coupled with the facts that twinning does not occur and four independent deformation modes are required25 (from self-consistent calculations) for extensive, crack-free flow, the plastic anisotropy leads to the build-up of internal stresses on the scale of the grain size. The stresses arise because grains favorably oriented for slip shed load to those less well oriented. The implication is that unless time is allowed for the internal stresses to relax, plastic flow will initiate cracks.26,27 If the cracks are tolerated, the ice will exhibit macroscopically ductile behavior. If not, then the material will exhibit macroscopically brittle behavior.
That ice can be brittle at temperatures right up to its melting point is perhaps surprising. The reason is related to the fact that its melting point diffusivity is around 10-15-10-14 m2/s, compared to higher values of 10-11-10-12 m2/s for elemental metals. Diffusion-assisted stress relaxation thus occurs relatively slowly.
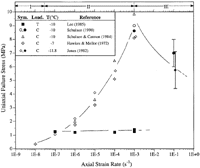 |
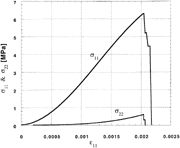
| Figure 4: Tensile and compressive strengths of equiaxed and randomly oriented fresh-water ice of about 1 mm grain size vs. strain rate. At the top of the figure, I, II, and III correspond to the stress-strain curves of Figure 3.30,48,78-80 |
 0.3(
0.3(

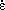 m) and the apparent activation energy27 Q ranges between 45 and 90 kJ/mol. (
m) and the apparent activation energy27 Q ranges between 45 and 90 kJ/mol. (

 memQ/RT), but is generally around 60 kJ/mol. At temperatures above -10°C, Q increases to 120-200 kJ/mol. in polycrystals. As expected for a dislocation-based process, confinement raises the compressive flow stress in the manner of a von Mises material,30-36 meaning that at failure the deviatoric component of the applied stress tensor is independent of the hydrostatic component. Brine inclusions
memQ/RT), but is generally around 60 kJ/mol. At temperatures above -10°C, Q increases to 120-200 kJ/mol. in polycrystals. As expected for a dislocation-based process, confinement raises the compressive flow stress in the manner of a von Mises material,30-36 meaning that at failure the deviatoric component of the applied stress tensor is independent of the hydrostatic component. Brine inclusions  3 vol.%, typical of first-year sea ice, lower the flow stress by a factor of two34,35 and increase the quasisteady-state creep rate by about an order of magnitude. Grain size is a factor only within very finely grained material37 where, for instance, refinement from 89 µm to 8 µm increases the steady-state creep rate at -37°C by a factor of 30 under a compressive stress of 1.4 MPa.
3 vol.%, typical of first-year sea ice, lower the flow stress by a factor of two34,35 and increase the quasisteady-state creep rate by about an order of magnitude. Grain size is a factor only within very finely grained material37 where, for instance, refinement from 89 µm to 8 µm increases the steady-state creep rate at -37°C by a factor of 30 under a compressive stress of 1.4 MPa.
Plastic flow and quasisteady-state creep of coarsely grained ice has been explained24,29 and then modeled quantitatively in terms of dislocation or power-law creep (i.e., by glide and climb of basal dislocations). Supporting this view is the fact that the activation energies for self-diffusion (0.65 eV = 62 kJ/mol.) and creep are essentially the same. Also, the creep rate is independent of grain size, and the dependence of the creep rate on stress (the inverse of the strain-rate sensitivity of the flow stress) is of the correct magnitude. The flow of very finely grained ice of micrometer dimensions can be rationalized in terms of grain-boundary sliding accommodated by dislocation creep. The effect of brine inclusions has been explained by a reduction in internal back stress.
Brittle failure under compression (regime CIII, Figures 3 and 4) is marked by sudden material collapse after shortening less than about 0.5%. The failure mode is generally shear faulting on planes inclined by about 30° to the direction of maximum principal stress, although axial splitting can also occur under unconfined loading. The material now exhibits strain-rate softening, but is still thermally softened. The brittle compressive strength rises sharply under a small amount of confinement in a Coulombic manner.42-47 This implies that the deviatoric stress at failure increases with increasing hydrostatic stress and means that frictional crack sliding is an important element in the failure process. Again, the strength decreases with increasing grain size in a Hall-Petch manner.48 Brine inclusions, however, have no effect at all.47
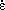 =v/2L
=v/2Lwhere v is the velocity of the ice relative to the structure, and L is the width of the structure. Typical values are v = 0.1- 1 m/s and L = 10-100 m, giving strain rates that lead to brittle behavior.
 |
 |
 |
| a | b | c |
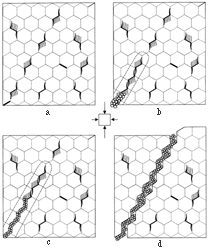
Figure 5: (a) A compressive shear fault in columnar-grained ice. The columns are perpendicular to the page and the fault runs from the upper right to the lower left. The ice was loaded biaxially such that the major stress ( 11) was vertical and the minor stress ( 11) was vertical and the minor stress ( 22) was horizontal. Note the wing cracks (arrowed) in the background field, the zigzag edges of the fault, and the milky zones stemming from one side of parent-inclined cracks (e.g., A and B). (b) A thin-section of the fault. Note the secondary or splay cracks stemming from parent cracks A and B. (c) A stress-strain curve for the above test specimen. (From Schulson, Iliescu, and Renshaw.51) 22) was horizontal. Note the wing cracks (arrowed) in the background field, the zigzag edges of the fault, and the milky zones stemming from one side of parent-inclined cracks (e.g., A and B). (b) A thin-section of the fault. Note the secondary or splay cracks stemming from parent cracks A and B. (c) A stress-strain curve for the above test specimen. (From Schulson, Iliescu, and Renshaw.51) |
||
Consider the most recent observations.51 Figure 5a shows a typical terminal shear fault; Figure 5b shows a thin section of the same fault, and Figure 5c shows the corresponding stress-strain curve. The fault was created by loading coarsely grained (10 mm) columnar fresh-water ice biaxially across the columns under a moderate degree of confinement (minor stress/major stress =  22/
22/ 11 = 0.1) at -10°C at 5 X 10-3 s-1. In Figure 5, the long axis of the grains is perpendicular to the page.
11 = 0.1) at -10°C at 5 X 10-3 s-1. In Figure 5, the long axis of the grains is perpendicular to the page.
 |
| Figure 6: A schematic sketch of the comb-crack mechanism. |
 = 26° to the maximum principal stress (vertical). Second, wing-cracks (arrowed) are distributed across the overall field of damage. They stem from the tips of intergranular parent cracks, which are inclined by about 45° to the direction of maximum principal stress and tend to be aligned with this direction. Third, the fault has zigzag edges, implying that wing cracks are an element in its structure. Fourth, milky features (e.g., A and B in Figure 5a) stem from one side of some parent-inclined cracks. These features are actually sets of closely spaced secondary cracks of about one-half the grain diameter, evident from the thin section (Figure 5b). These are termed splay cracks in recognition of the term used to describe similar features in faulted rock.52-55
= 26° to the maximum principal stress (vertical). Second, wing-cracks (arrowed) are distributed across the overall field of damage. They stem from the tips of intergranular parent cracks, which are inclined by about 45° to the direction of maximum principal stress and tend to be aligned with this direction. Third, the fault has zigzag edges, implying that wing cracks are an element in its structure. Fourth, milky features (e.g., A and B in Figure 5a) stem from one side of some parent-inclined cracks. These features are actually sets of closely spaced secondary cracks of about one-half the grain diameter, evident from the thin section (Figure 5b). These are termed splay cracks in recognition of the term used to describe similar features in faulted rock.52-55
Experiments and analyses have shown that the parent cracks nucleate through grain-boundary sliding.56-59 The wing cracks initiate as a result of frictional sliding of the parent cracks.50 The splay cracks, it is thought, initiate from Hertzian contact stresses across the parent-crack faces and then propagate within a tensile field created most likely by nonuniform displacements across the sliding crack.
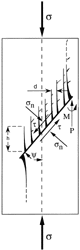
Schulson et al.51 propose that splay cracks are critical features in initiating the fault. Upon forming, they create sets of closely spaced microcolumns fixed on one end and free on the other. The free end contacts the sliding crack, which induces a moment that causes the columns to bend and break, rather like the breaking of teeth in a comb under a sliding thumb (Figure 6). It is the failure of these microcolumns under frictional shear loading, they suggest, that initiates the fault. Near-surface microcolumns probably break first, owing to less constraint there. It is imagined that growth then follows along a band of reduced shear strength that is composed of splay cracks formed prior to fault initiation plus fresh splay cracks created within a kind of process zone just ahead of the advancing fault front (Figure 7). The front moves rapidly across the section, creating "gouge" in its wake.
An estimate of the stress to initiate the fault may be obtained as follows. Assume that the fault is initiated when a microcolumn breaks. Assume also the scenario sketched in Figure 6, where M and P, respectively, are the induced moment and axial load per unit depth of the microcolumn;  and
and  n are the shear stress and normal stresses, respectively, acting on the microcolumn; and
n are the shear stress and normal stresses, respectively, acting on the microcolumn; and 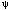 is the inclination of the parent crack. Then, by invoking the analysis of Thouless et al.60 for the propagation of an edge crack in a brittle plate, one can show that for
is the inclination of the parent crack. Then, by invoking the analysis of Thouless et al.60 for the propagation of an edge crack in a brittle plate, one can show that for 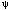 = 45° the initiation stress,
= 45° the initiation stress,  f, under uniaxial loading is approximated by the relationship51
f, under uniaxial loading is approximated by the relationship51
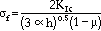
 |
| Figure 7: A schematic of the proposed development of a compressive shear fault, from a point very close to terminal failure. The hexagonal network denotes the microstructure. Wing cracks sprout from the tips of some inclined, intergranular cracks, and splay cracks stem from one side of some of the parent cracks. The fault grows through a kind of process zone and creates gouge in its wake as splay-crack-induced microcolumns break. (From Schulson, Iliescu, and Renshaw.51) |
 is the slenderness ratio of the microcolumns; and h is their length. Taking61 KIc = 0.1 MPa·m0.5 and µ = 0.5862 and using (from these observations)
is the slenderness ratio of the microcolumns; and h is their length. Taking61 KIc = 0.1 MPa·m0.5 and µ = 0.5862 and using (from these observations)  = 5.3 ±2 and h = D/2, where D is the grain size, the estimated initiation stress (lower limit) is 1.0 ±0.5 MPa. The actual uniaxial strength for coarsely grained ice is about two to three times this estimate. The difference may reside in the fact that the model ignores crack/crack interactions and column/column frictional interactions. Nevertheless, it gives the correct order of magnitude of the strength, and it captures the (grain size)-0.5 dependence of the compressive failure stress by relating the microcolumn length to the grain size. Also, through the effects of temperature and sliding speed on the friction coefficient,62 the model correctly captures the magnitudes of both thermal and strain-rate softening.
= 5.3 ±2 and h = D/2, where D is the grain size, the estimated initiation stress (lower limit) is 1.0 ±0.5 MPa. The actual uniaxial strength for coarsely grained ice is about two to three times this estimate. The difference may reside in the fact that the model ignores crack/crack interactions and column/column frictional interactions. Nevertheless, it gives the correct order of magnitude of the strength, and it captures the (grain size)-0.5 dependence of the compressive failure stress by relating the microcolumn length to the grain size. Also, through the effects of temperature and sliding speed on the friction coefficient,62 the model correctly captures the magnitudes of both thermal and strain-rate softening.
It is not a new idea that failure of deformation-induced microcolumns is the micromechanical event accounting for the initiation of a shear fault. Others have advanced a similar view.63-65 Previously, however, failure was imagined to occur by elastic buckling of columns fixed on both ends, created, for instance, by echelon arrays of wing cracks. Given the dimensions of the splay-induced microcolumns created in ice, the Euler buckling stress is estimated to be 630 MPa to 3,000 MPa, and this is two to three orders of magnitude greater than the strength of the material. Hence, it is our opinion that elastic buckling is not the event that triggers the fault.
The transition can be understood in terms of the competition between stress relaxation and stress build-up at crack tips. At intermediate rates of deformation crack-tip stresses relax through creep deformation, and so the mode-I stress intensity factor KI, at either the tips of wing cracks or splay cracks, never reaches the critical level. At high rates, on the other hand, stress build-up dominates, and KI quickly reaches the critical level Kic. The transition occurs when the competition between stress relaxation and stress build-up is in balance.
Schulson34,48 modeled the process by invoking Ashby-Hallam63 frictional sliding-crack mechanics and Riedel-Rice66 crack-tip creep. By assuming that cracks propagate when the crack-tip creep zone size falls below a small fraction f of the crack length, he obtained the transition strain rate in terms of the independently measurable parameters of fracture resistance (KIc,), creep constant B, (
 B
B  1/m) friction (µ), and crack length (D); f must be calculated from the Riedel-Rice model. The transition strain rate may then be expressed by the relationship
1/m) friction (µ), and crack length (D); f must be calculated from the Riedel-Rice model. The transition strain rate may then be expressed by the relationship
 |
| a |
 |
| b |
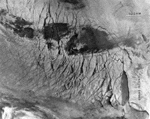
| Figure 8: (a) A satellite image of large cracks, termed "leads," in the Arctic sea-ice cover. Note the general alignment of the pattern and the wing-like cracks (two are arrowed). (From Schulson and Hibler.70) (b) Wing cracks formed within columnar ice loaded to failure in the laboratory. The major stress was vertical and the minor stress (0.05 of major stress) was horizontal. (From Iliescu and Schulson [unpublished].) |
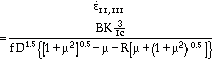
where R is the ratio of the confining stress to the most compressive stress. A comparison with experiment34,35,67 shows that the model correctly captures the effects of crack size (set by grain size68 in virgin material), confinement, and brine pores and that it predicts for the conditions of Figure 4 a transition strain rate of 10-3 s-1, which is close to that observed. The model also holds that through the effects of temperature on friction and creep, the transition strain rate is only slightly dependent upon temperature, at least over the range -40°C to -3°C, again in accord with experiment. Moreover, by including the crack size, the model accounts for the fact that sheets of first-year sea ice, which are laced with meter-sized (and larger) cracks and wind loaded under compression, exhibit macroscopic brittle behavior69 even though they are deformed at rates as low as 10-7 s-1.
Moreover, there is new evidence72 that fracturing and fragmentation of ice exhibit fractal organization in the lab and in the field. Within faulted rock, both splay cracks (as noted above) and zigs and zags denoting wing cracks73,74 have been seen on small and large scales. While the physics may not change with size, the terminal compressive failure stresses will probably be lower in larger features, possibly scaling as (crack size)-0.5. Consistent with this notion, at least for ice, is Sanderson's4 observation that large fractures fail at lower stresses than small ones. Also consistent are recent measurements of stresses within floating covers,71,75 which are usually within the kPa range as compared with the MPa range of lab measurements. The ductile flow of glaciers, on the other hand, reflects the power-law creep relationship of small test specimens, implying that dislocation-based processes are scale-independent.
Failure under tension is size-dependent, owing in part to the larger flaws within the larger features. Dempsey76,77 has discussed this aspect of the subject, from the perspective of applied mech-anics.
References
1. M.F. Perutz, J. Glaciol., 1 (1948), p. 95.
2. P.V. Hobbs, Ice Physics (London: Oxford University Press, 1974).
3. V.F. Petrenko and R.W. Whitworth, Physics of Ice (London: Oxford University Press, in press).
4. T.J.O. Sanderson, Ice Mechanics Risks to Offshore Structures (London: Graham & Trotman, 1988).
5. W.F. Weeks, Physics of Ice-Covered Seas, ed. M. Leppäranta (Helsinki: Helsinki University Printing House, 1998), pp. 1-24 and 25-104.
6. B. Michel, Ice Mechanics (Quebec, Canada: Les Presses de l'Université Laval, 1978).
7. R.J. Arsenault et al., eds., Johannes Weertman Symposium (Warrendale, PA: TMS, 1996).
8. T.B. Curtin, Naval Research Reviews L, Arctic Studies (1998), p. 6.
9. B.G. Levi, Physics Today (November 1998), p. 17.
10. W.B. Durham, S. Kirby, and L.A. Stern, J. Geophys. Res., 102 (1997), p. 16293.
11. L. Pauling, J. American Chemical Society, 57 (1935), p. 2680.
12. J.D. Bernal and R.H. Fowler, J. Chem. Physics, 1 (1933), p. 515.
13. J.W. Glen, Cold Regions Science and Technology, Monograph II-C2a (Hanover, NH: U.S. Army Corps. of Engineers, 1974).
14. T. Hondoh et al., J. Chem. Physics, 87 (1983), p. 4044.
15. N. Bjerrum, Det Kongelige Danske Videnskabernes Selskab Matematisk-fysiske Meddeleiser, 27 (1951), p. 56.
16. F. Liu, I. Baker, and M. Dudley, Phil. Mag. A, 71 (1995), p. 15.
17. R.W. Whitworth, Phil. Mag. A, 41 (1980), p. 521.
18. J.W. Glen, Phys. Kondens. Mater., 7 (1968), p. 43.
19. M. Oguro and A. Higashi, Physics and Chemistry of Ice, ed. E. Whalley, S.J. Jones, and L.W. Gold (Ottawa, Canada: Royal Society of Canada, 1973), p. 33.
20. J.F. Nye, Physics and Chemistry of Ice, ed. N. Maeno and T. Hondoh (Sapporo, Japan: Hokkaido University Press, 1992), pp. 200-205.
21. S. de la Chapelle et al., J. Geophys. Res., 103 (1998), p. 5091.
22. W.F. Weeks and A.J. Gow, J. Geophys. Res., 84 (1978), p. 5105.
23. N.H. Fletcher, The Chemical Physics of Ice (New York: Cambridge University Press, 1970), p. 271.
24. P. Duval, M.F. Ashby, and I. Anderman, J. Phys. Chem., 87 (1983), p. 4066.
25. J.W. Hutchinson, Metall. Trans. A, 8 (1977), p. 1465.
26. L.W. Gold, Canadian J. of Physics, 44 (1966), p. 2757.
27. L.W. Gold, Phil. Mag., 26 (1972), p. 311.
28. N.K. Sinha, J. Materials Sci., 23 (1988), p. 4415.
29. J. Weertman, Annu. Rev. Earth Planet Sci., 11 (1983), p. 215.
30. S.J. Jones, J. Glaciol., 28 (1982), p. 171.
31. J.-P. Nadreau and B. Michel, Cold Regions Science and Technology, 13 (1986), p. 75.
32. R. Frederking, J. Glaciol., 18 (1977), p. 505.
33. J.A. Richter-Menge, J. Offshore Mechanics and Arctic Engineering, 113 (1991), p. 344.
34. E.M. Schulson and S.E. Buck, Acta Metall., 43 (1995), p. 3661.
35. E.M. Schulson and O.Y. Nickolayev, J. Geophys. Res., 100 (1995), p. 22383.
36. J.S. Melton and E.M. Schulson, J. Geophys. Res., 103 (1998), p. 21759.
37. D.L. Goldsby and D.L. Kohlstedt, Scripta Materialia, 37 (1997), p. 1399.
38. E.M. Schulson et al., J. Materials Sci. Ltrs. 8 (1989), p. 1193.
39. E.M. Schulson, P.N. Lim, and R.W. Lee, Phil. Mag. A, 49 (1984), p. 353.
40. J.A. Richter-Menge and K.F. Jones, J. Glaciol., 39 (1993), p. 609.
41. E.M. Schulson, S.G. Hoxie, and W.A. Nixon, Phil. Mag. A, 59 (1989), p. 303.
42. T.R. Smith and E.M. Schulson, Acta Metall., 41 (1993), p. 153.
43. R.E. Gagnon and P.H. Gammon, J. Glaciol., 41 (1995), p. 528.
44. M.A. Rist and S.A.F. Murrell, J. Glaciol., 40 (1994), p. 305.
45. J. Weiss and E.M. Schulson, Acta Metall., 43 (1995), p. 2303.
46. E.T. Gratz and E.M. Schulson, J. Geophys. Res., 102 (1997), p. 5091.
47. E.M. Schulson and E.T. Gratz, Acta Metall. (in press).
48. E.M. Schulson, Acta Metall., 38 (1990), p. 1963.
49. S.K. Singh and I.J. Jordaan, Cold Regions Science and Technology, 24 (1996), p. 153.
50. B. Zou, J. Xiao, and I.J. Jordann, Cold Regions Science and Technology, 24 (1996), p. 213.
51. E.M. Schulson, D. Iliescu, and C.E. Renshaw, J. Geophys. Res. (in press).
52. T.-F. Wong, Int. J. Rock Mech. Min. Sci. Geomech. Abstr., 19 (1982), p. 49.
53. R.R. Gottschalk et al., J. Geophys. Res., 95 (1990), p. 21613.
54. S.J. Martel and D.D. Pollard, J. Geophys. Res., 94 (1989), p. 9417.
55. K.M. Cruikshank et al., J. Struct. Geol., 13 (1991), p. 865.
56. H.J. Frost, Proc. in Joint Applied Mechanics and Materials Summer Conference, ed. J.P. Dempsey and Y.D.S. Rajapakse (Los Angeles, CA: University of California, 1995), pp. 1-8.
57. R.C. Picu, V. Gupta, and H.J. Frost, J. Geophys. Res., 99 (1994), p. 11775.
58. R.C. Picu and V.J. Gupta, Acta Metall., 43 (1995), p. 3791.
59. J. Weiss, E.M. Schulson, and H.J. Frost, Phil. Mag. A, 73 (1996), p. 1385.
60. M.D. Thouless et al., Acta Metall., 35 (1987), p. 1333.
61. J.P. Dempsey, Ice Structure Interactions, ed. S.J. Jones (New York: Springer-Verlag, 1991), p. 109.
62. D.E. Jones, F.E. Kennedy, and E.M. Schulson, Ann. Glaciol., 15 (1991), p. 242.
63. M.F. Ashby and S.D. Hallam, Acta Metall., 34 (1986), p. 497.
64. C.G. Sammis and M.F. Ashby, Acta Metall., 34 (1986), p. 511.
65. Z.P. Bazant and Y. Xiang, J. Eng. Mech., 2 (1997), p. 162.
66. H. Riedel and J.R. Rice, ASTM-STP-7700, (1980), p. 112.
67. R.A. Batto and E.M. Schulson, Acta Metall., 41 (1993), p. 2219.
68. D.M. Cole, Proc. Fourth Int. Symp. on Offshore Mech. Arctic Engng. (New York: ASME, 1985), p. 220.
69. J.R. Marko and R.E. Thomson, J. Geophys. Res., 82 (1977), p. 979.
70. E.M. Schulson and W.D. Hibler, III, J. Glaciol., 37 (1991), p. 319.
71. J.A. Richter-Menge et al., Proc. of the ASYS Conference on the Dynamics of the Arctic Climate System, ed. P. Lemke (Gotteborg, Sweden: World Meterological Org., 1996), pp. 327-331.
72. J. Weiss and M. Gay, J. Geophys. Res., 103 (1998), p. 24005.
73. D.E. Moore and D.A. Lockner, J. Struct. Geol., 17 (1995), p. 95.
74. R. Bilham and P. Williams, Geophys. Res. Lett., 12 (1985), p. 557.
75. W.B. Tucker, III and D.K. Perovich, Cold Regions Science and Technology, 20 (1992), p. 119.
76. J.P. Dempsey, contribution to Research Trends in Solid Mechanics, a report from U.S. National Committee on Theoretical and Applied Mechanics (in press).
77. J.P. Dempsey, Johannes Weertman Symposium, ed. R.J. Arsenault et al. (Warrendale, PA: TMS, 1996), p. 351.
78. R.W. Lee (M.S. thesis, Thayer School of Engineering, Dartmouth College, 1985).
79. E.M. Schulson and N.P. Cannon, Proc. IAHR Ice Symp. (Hamburg, Germany: Hamburgische, Schiffbau-Versuchanstahlt GmbH, 1984), p. 24.
80. I. Hawkes and M. Mellor, J. Glaciol., 11 (1972), p. 103.
ABOUT THE AUTHOR
E.M. Schulson is currently a professor of engineering at Thayer School of Engineering at Dartmouth College.
For more information, contact E.M. Schulson, Thayer School of Engineering, Dartmouth College, Hanover, New Hampshire 03755; (603) 646-2888; fax (603) 646-3856; e-mail erland.schulson@dartmouth.edu.
Direct questions about this or any other JOM page to jom@tms.org.
| Search | TMS Document Center | Subscriptions | Other Hypertext Articles | JOM | TMS OnLine |
|---|