 |
|
|---|
 |
|
|---|
 |
|---|
| CONTENTS |
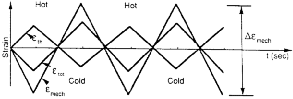
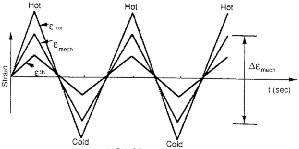
In TMF tests, a specimen is subjected to a desired temperature and mechanical strain with different phasings. Two baseline TMF tests are conducted in the laboratory with proportional phasings: in-phase (IP), the maximum strain at the maximum temperature, and out-of-phase (OP), the maximum strain at the minimum temperature. The variation of thermal, mechanical, and total strain components with time in OP and IP cases is illustrated in Figure 1. These two types of phasings reproduce many of the mechanisms that develop under TMF. The mechanical strain ( mech) is the sum of the elastic and inelastic strain components, while the total strain (
mech) is the sum of the elastic and inelastic strain components, while the total strain ( tot or
tot or  t) is the sum of thermal and mechanical strain components
t) is the sum of thermal and mechanical strain components
 tot= tot=
 th+ th+
 mech= mech=
 (T-T0)+ (T-T0)+
 mech mech |
(1) |
where  th is the thermal strain, T0 is the reference temperature where the test was begun, T is the test temperature, and
th is the thermal strain, T0 is the reference temperature where the test was begun, T is the test temperature, and  is the coefficient of thermal expansion.
is the coefficient of thermal expansion.
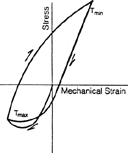
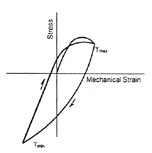
A schematic of the stress-strain behavior corresponding to TMF-OP and TMF-IP cases is illustrated in Figure 2. In the TMF-OP case, the material undergoes compression at high temperatures and tension at low temperatures. The inverse behavior is observed for the TMF-IP case. The mean stress of the cycle is tensile in the TMF-OP case, while it is compressive in the TMF-IP case.
 |
|
| a | |
 |
|
| b | |
| Figure 1. Strain versus time under (a) TMF-OP and (b) TMF-IP cases.3 | |
 |
 |
| a | b |
| Figure 2. Stress versus strain under (a) TMF-OP and (b) TMF-IP cases.1 | |
Under TMF conditions, damage mechanisms prevalent in metals involve three major aspects: fatigue, environmental (oxidation), and creep damage. These damage mechanisms may act independently or in combination according to various materials and operating conditions, such as maximum and minimum temperatures, temperature range, mechanical strain range, strain rate, the phasing of temperature and strain, dwell time, or environmental factors.
Traditionally, fatigue damage is the cyclic plasticity-driven, time- and temperature-independent damage that exists whenever cyclic loading occurs. Creep refers to a material undergoing viscous deformation at a constant stress level. This type of deformation leads to intergranular creep cavity growth and rupture. Under TMF loading, however, creep deformation contributes to the formation and propagation of microcracks. Metals exposed to environments at high temperatures are subjected to corrosion by oxidation. This kind of corrosion is accelerated by a tensile stress. During TMF, brittle oxides can enhance the nucleation and propagation of fatigue microcracks and impede the rewelding of crack surfaces during unloading.
Due to complexity, a well-accepted framework for the prediction of TMF life has been elusive. Various approaches have been taken, ostensibly nonisothermal generalizations of isothermally derived models.
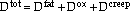 |
(2) |
Assuming that linear damage is equal to one at failure, the equation may be rewritten in terms of the life, Nf, where damage is taken as equal to 1/Nf,
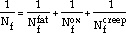 |
(3) |
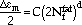 |
(4) |
where 
 m is the mechanical strain range, and C and d are material constants determined from low-temperature isothermal tests.
m is the mechanical strain range, and C and d are material constants determined from low-temperature isothermal tests.
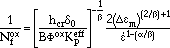 |
(5) |
where hcr is a critical crack length at which the environmental attack trails behind the crack-tip advance,  0 is the ductility of the environmentally affected material, B is the coefficient,
0 is the ductility of the environmentally affected material, B is the coefficient,  is the exponent, and
is the exponent, and  is the strain-rate sensitivity constant. The values of all above constants are determined by experiments.
is the strain-rate sensitivity constant. The values of all above constants are determined by experiments.  ox is a phasing factor for environmental damage and is defined as
ox is a phasing factor for environmental damage and is defined as
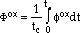 |
(6) |
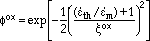 |
(7) |
where is the ratio of thermal to mechanical strain rates, and
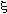 ox is a constant as a measure of the relative amount of oxidation damage for different thermal strain to mechanical strain ratios and is extracted from the experiments. Kpeff is a parabolic oxidation constant and can be calculated by
ox is a constant as a measure of the relative amount of oxidation damage for different thermal strain to mechanical strain ratios and is extracted from the experiments. Kpeff is a parabolic oxidation constant and can be calculated by
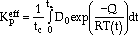 |
(8) |
where T(t) is the temperature as a function of time, tc is the cycle period, D0 is the diffusion coefficient for oxidation, Q is the activation energy for oxidation, and R is the gas constant.
 |
(9) |
where is the effective stress,
 H is the hydrostatic stress, K is the drag stress,
H is the hydrostatic stress, K is the drag stress,  1 and
1 and  2 are scaling factors that represent the relative amount of damage occurring in tension and compression,
2 are scaling factors that represent the relative amount of damage occurring in tension and compression,  H is the activation energy for the rate-controlled creep mechanism, and A and m are material constants.
H is the activation energy for the rate-controlled creep mechanism, and A and m are material constants.
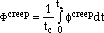 |
(10) |
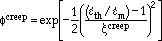 |
(11) |
the constant, 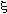 creep, defines the sensitivity of the phasing to the creep damage.
creep, defines the sensitivity of the phasing to the creep damage.
This model couples a viscoplastic, nonisothermal constitutive model of material under investigation with an incremental evolution of damage for oxidation and creep terms within a TMF loading cycle. The model was applied to MAR-M247 and 1070 steel,1,5,6 and 80% of the predictions were within a factor of ± 2.5 of the experimentally measured lives.
The general form of the equation is
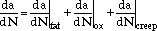 |
(12) |
where a is the crack length, and N is the cycle number.
The fatigue component of microcrack propagation is correlated using the  J parameter
J parameter
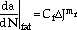 |
(13) |
where mf and Cf are constants. If  J is taken as
J is taken as
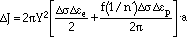 |
(14) |
where 
 is the stress range and
is the stress range and 
 e and
e and 
 p are the elastic and plastic strain ranges, respectively, n' is the cyclic-hardening exponent, Y is a geometric correction factor, and a is the crack length. The function f(1/n') is given by
p are the elastic and plastic strain ranges, respectively, n' is the cyclic-hardening exponent, Y is a geometric correction factor, and a is the crack length. The function f(1/n') is given by
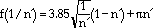 |
(15) |
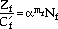 |
(16) |
where
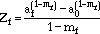 if mf if mf  1. 1. |
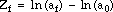 if mf = 1 if mf = 1 |
(17) |
= 2
 Y2Cf, a0 and af are the initial and final crack sizes, respectively, and
Y2Cf, a0 and af are the initial and final crack sizes, respectively, and  is defined as
is defined as
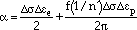 |
(18) |
The creep component of the microcrack propagation is correlated using the stress power-release-rate parameter, ,
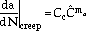 |
(19) |
where Cc and mc are the experimentally determined creep constant and exponent, respectively.
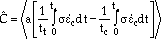 |
(20) |
where is the creep strain rate, tt is the time within a cycle during which tensile strain accumulates, and tc is the time within a cycle during which compressive strain accumulates. The Macaulay brackets, < >, are defined as
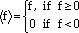 |
(21) |
The creep strain rate, , is determined using a viscoplastic constitutive law for the material under investigation.
The oxidation component of the microcrack propagation is also correlated using the  J parameter with an additional time and temperature dependence
J parameter with an additional time and temperature dependence
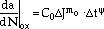 |
(22) |
where m0 and 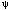 are experimentally determined constants,
are experimentally determined constants,  t is the cycle time, and the coefficient, C0, is defined as
t is the cycle time, and the coefficient, C0, is defined as
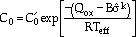 |
(23) |
where , B, and k are experimentally determined constants; Qox is the experimentally measured activation energy of the effective crack-tip oxidation and growth process; the parameter
= <
 Tmin>; and
Tmin>; and  Tmin is the stress at the minimum temperature. Teff is an effective temperature and is defined as
Tmin is the stress at the minimum temperature. Teff is an effective temperature and is defined as
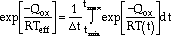 |
(24) |
where tmin and tmax are the times at which the minimum and maximum temperatures occur during a temperature cycle, respectively, and  t = tmax - tmin.
t = tmax - tmin.
 |
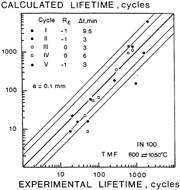 |
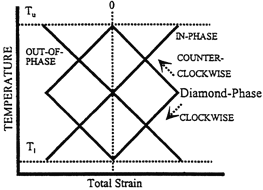
| Figure 3. Temperature-strain cycles for different TMF tests (Tu—upper temperature, Tl—low temperature).2 | Figure 4. A comparison between calculated lives to a 0.1 mm deep crack in TMF of bare IN-100 specimens and experimental data.10 |
Among the damage-rate models is one proposed by Reucket and Remy, which accounts for the interactions between fatigue and oxidation by superimposing both kinds of damages.8–10
The model considers that TMF damage in conventionally cast superalloys is mostly the growth of a dominant microcrack and that the initiation period can be neglected for practical purposes. Thus, the damage equations were derived assuming that the elementary crack growth results from an advance associated with crack opening under fatigue and from an additional contribution due to oxidation at the crack tip. The damage equation can be written as
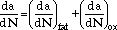 |
(25) |
The fatigue contribution to the crack advance is estimated assuming that the crack is opened only by a tensile stress
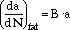 |
(26) |
where
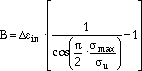 |
(27) |
where 
 in is the inelastic strain range,
in is the inelastic strain range,  max is the maximum cyclic tensile stress, and
max is the maximum cyclic tensile stress, and  u is the ultimate tensile strength in monotonic tension.
u is the ultimate tensile strength in monotonic tension.
The contribution to crack advance due to oxidation is derived assuming that fracture of the formed oxide spike occurs at each tensile stroke. The oxidation rate at the crack tip is measured by the depth of interdendritic oxide spikes formed before fracture,  lox,
lox,
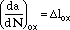 |
(28) |
The interdendritic oxidation obeys a t1/4 kinetics, where t is time,
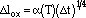 |
(29) |
where  t is the cycle period, and
t is the cycle period, and
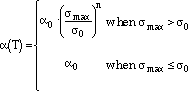 |
(30) |
where  0 is the oxidation constant at a given temperature,
0 is the oxidation constant at a given temperature,  0 is a threshold (above this threshold, the depth of oxide formed at every cycle increases with the maximum stress according to a power law, Equation 30), and n is the exponent. These parameters are identified from tensile tests and some metallographic measurements of crack depth for the specimens.
0 is a threshold (above this threshold, the depth of oxide formed at every cycle increases with the maximum stress according to a power law, Equation 30), and n is the exponent. These parameters are identified from tensile tests and some metallographic measurements of crack depth for the specimens.
Under TMF, as temperature varies, the right side of Equation 29 has to be averaged over the cycle, and an average oxidation constant, , is computed as
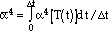 |
(31) |
By Equations 25-28, the following equation can be derived for the crack depth, a, as a function of the number of cycles, N:
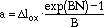 |
(32) |
or the number of cycles, N, corresponding to a given crack depth, a,
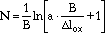 |
(33) |
Equation 32 or 33 can be used for TMF life prediction with good results.
Remy and colleagues have proposed another fatigue-damage model applicable to TMF, which also assumes that fatigue life is spent in the growth of microcracks.10 The oxidation and fatigue interaction are considered in the following manner: exposure to high temperatures during the TMF cycle oxidizes the material at the crack tip; then, high stress ranges at medium temperatures give rise to fatigue damage in the material that has been embrittled by oxidation.
Consider a volume element of size,  , ahead of the crack tip. This volume element will endure an incremental damage, dD, during dN cycles under oxidizing and cyclic-loading conditions. This damage increment is given by
, ahead of the crack tip. This volume element will endure an incremental damage, dD, during dN cycles under oxidizing and cyclic-loading conditions. This damage increment is given by
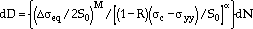 |
(34) |
with R = 1 - 
 yy/
yy/ yy when
yy when 
 yy
yy 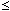
 yy, and R = 0 when
yy, and R = 0 when 
 yy >
yy >  yy, where
yy, where 
 eq is the Von Mises equivalent stress range averaged over the microstructural element at the crack tip;
eq is the Von Mises equivalent stress range averaged over the microstructural element at the crack tip;  yy is the maximum tensile value of the normal stress of the crack tip at a distance
yy is the maximum tensile value of the normal stress of the crack tip at a distance  ; S0, M, and
; S0, M, and  are constants at a given temperature; and
are constants at a given temperature; and
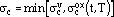 |
(35) |
where is the critical fracture stress (i.e., the critical value of
 yy when N approaches infinity) of the virgin alloy, and
yy when N approaches infinity) of the virgin alloy, and  cox is that of the alloy embrittled by oxidation, which is defined as
cox is that of the alloy embrittled by oxidation, which is defined as
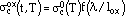 |
(36) |
where is a constant at a given temperature; the function, f, is determined from the experiments; and
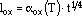 |
(37) |
where t is the exposure time at a given temperature, and  ox is an oxidation constant.
ox is an oxidation constant.
When the temperature varies, the right side of Equation 37 has to be averaged over the cycle, and an average oxidation constant, ox, is computed as
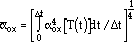 |
(38) |
where  t is the cycle period.
t is the cycle period.
Using Equations 35 and 36,  c is computed at every cycle, and the number of cycles to break the volume element will be given by the condition
c is computed at every cycle, and the number of cycles to break the volume element will be given by the condition
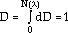 |
(39) |
N( ) is, thus, computed through the set of Equations 34-37 using an iterative procedure, cycle by cycle, until the condition of Equation 39 is fulfilled. The model gives good predictions of lives for an in-phase cycle when using a diamond-shaped cycle (Figure 4).
) is, thus, computed through the set of Equations 34-37 using an iterative procedure, cycle by cycle, until the condition of Equation 39 is fulfilled. The model gives good predictions of lives for an in-phase cycle when using a diamond-shaped cycle (Figure 4).
An engineering procedure for TMF crack-growth-rate predictions is presented by Dai and colleagues, which is based on isothermal data.11 The model uses a linear summation of the contributions to crack growth of the two dominant mechanisms, which are active at minimum and maximum temperatures of the cycle—namely, the mechanical fatigue and environmentally assisted crack growth
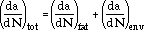 |
(40) |
where (da/dN)fat, the mechanical fatigue contribution, is correlated by a fracture mechanics parameter,  Keff
Keff
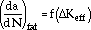 |
(41) |
where the correlated function, f, is determined by isothermal or TMF tests. Assuming that the cracks were opened when the loads were tensile,
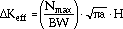 |
(42) |
where Nmax is the peak value of the measured load during cycling, a is the crack length measured from the specimen edge, B is the thickness of the specimen, W is the width of the specimen, and H is the geometrical function that characterizes the single-edge notched (SEN) specimen geometry as well as the boundary conditions.
(da/dN)env is the time-dependent contribution related to the kinetics of oxygen-induced embrittlement. For TMF, it is computed using
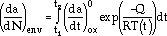 |
(43) |
where is a material constant, Q is the apparent activation energy for oxygen transport, T is the temperature in oK, and t1 and t2 pertain to the starting and finishing times within one cycle where oxygen-induced embrittlement operates. Assuming that t1 and t2 are related to the opening and closure processes of the crack, the time-dependent contributions (Equation 43) were estimated by integrating over the tensile load part of the cycle. Combining Equation 41 (mechanical fatigue) with Equation 43 (contribution of oxygen-induced embrittlement) allows the accurate prediction of the actual crack growth rates (da/dN)tot.
 |
 |
 |
 |
| a | b | c | d |
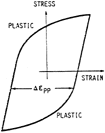
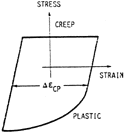
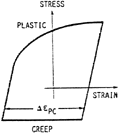
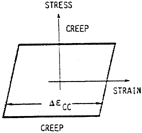
| Figure 5. SRP cycle types showing (a) pp type, (b) cp type, (c) pc type, and (d) cc type cycles.18 | |||
For each of the inelastic deformation types, a life relation is established, typically given as
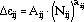 |
(44) |
where Aij and aij, i,j = p, c (i.e., pp, cp, pc, and cc modes) are material-dependent parameters. When these modes are present in a complex cycle, their damaging effects may be combined by the use of the interaction damage rule (IDR), and a calculation for the life is performed. The IDR can be stated as
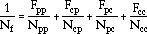 |
(45) |
where Fpp, Fcp, Fpc, and Fcc correspond to the relative amount of inelastic-strain type present (e.g., 
 pp/
pp/
 in,
in, 
 cp/
cp/
 in,
in, 
 pc/
pc/
 in, and
in, and 
 cc/
cc/
 in), and the terms Npp, Ncp, Npc, and Ncc, correspond to the life levels established from Equation 44 at the inelastic strain range,
in), and the terms Npp, Ncp, Npc, and Ncc, correspond to the life levels established from Equation 44 at the inelastic strain range, 
 in.
in.
SRP has since been successfully formulated on a total strain basis (TS-SRP), extending it into the isothermal low-strain, long-life regime where the inelastic strains are small and difficult to determine. This extension, plus the introduction of the bithermal test to characterize TMF behavior, has permitted the SRP method to be applied to general TMF life prediction problems.14–16 (Bithermal experiments utilized a trapezoidal-wave temperature versus time profile wherein mechanical straining was imposed only during the isothermal portions at the maximum and minimum temperatures. Moreover, during the bithermal tests, the temperature was changed while the specimen was held at zero load.)
Fractographic and metallographic investigations were conducted on the specimens of some materials, such as Haynes 188, that were fatigued to failure under IP and OP bithermal and thermomechanical loading conditions. These investigations identified the prevailing damaging mechanisms in both bithermal and thermomechanical fatigue tests. For these identified materials, bithermal fatigue tests could be used as the basis for TMF life prediction.
Total Strain Range-Life Relations
The total strain range is the sum of two terms, 
 e and
e and 
 in. Each term is a power law function of Nf0 (the subscript 0 on Nf denotes the fatigue life for an equivalent zero mean stress condition) and appears as one of a family of straight lines on the log-log coordinates of Figure 6. The solid lines represent upper and lower bounds on the inelastic and elastic strain-range terms. The equation for the general life relation is shown in Figure 6 and is written as
in. Each term is a power law function of Nf0 (the subscript 0 on Nf denotes the fatigue life for an equivalent zero mean stress condition) and appears as one of a family of straight lines on the log-log coordinates of Figure 6. The solid lines represent upper and lower bounds on the inelastic and elastic strain-range terms. The equation for the general life relation is shown in Figure 6 and is written as
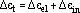 |
(46) |
or
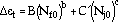 |
(47) |
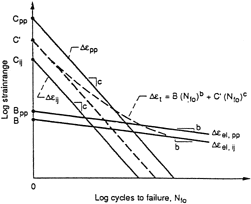 |
| Figure 6. A schematic of strain range-life relations for the total strain version of strain-range partitioning.14 |
The intercepts, B and C', are first-order functions of many of the variables (e.g., time per cycle, strain rate, environment, wave shape, and temperature) that are known to influence TMF lives. For example, both B and C' typically decrease as the time per cycle increases (lower frequency, lower strain rate, or increased hold-time), since this introduces the phenomena of creep and environmental attack. Creep and environmental attack are usually regarded as detrimental damage mechanisms. As temperature increases, B usually decreases (primarily due to creep-weakening effects, but also due to environmental attack), and C' may do either.
Inelastic Strain Range-Life Relations
The intercept, C', is evaluated as
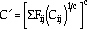 |
(48) |
where ij = pp, pc, or cp, and Fij is the fractional value of each inelastic strain range present in any given TMF cycle (i.e., the partitioning of 
 in).
in).
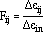 |
(49) |
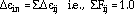 |
(50) |
(i.e., 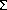 Fij = 1.0). Fij can be written as an exponential relation of the time per cycle, normalized by a function of the total strain range
Fij = 1.0). Fij can be written as an exponential relation of the time per cycle, normalized by a function of the total strain range
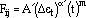 |
(51) |
The constants, A',  ', and m, are determined from multiple regression analyses of analytical data.
', and m, are determined from multiple regression analyses of analytical data.
If a viscoplastic model for a material has not been evaluated, the IP and OP bithermal pp, cp, and pc tests would be utilized to measure Fij and determine the constants, A',  , and m.
, and m.
In addition to Fij, the other factors influencing the value of C' are Cij and c. Bithermal fatigue test results provide the data base to determine the constants, Cij and c.
Elastic Strain Range-Life Relations
In the elastic strain-range versue life relations, the exponent, b, was determined from bithermal experiments. The intercept, B, is expressed as
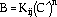 |
(52) |
where n is the cyclic strain-hardening exponent, and n is related to b and c by the expression n = b/c. Kij is a time-dependent, elastic-modulus-normalized cyclic strength coefficient defined by
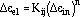 |
(53) |
The relation between Kij and cycle time can be expressed as
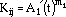 |
(54) |
Normally, the values of the constants, A1' and m1, are ascertained using a viscoplastic model or the least-squares curve fit of the bithermal test data.
For the specific conditions of the cycle, the intercepts, B and C', and the exponents, b and c, will be evaluated. Then the total strain range versus cyclic life failure curve will be established, and the TMF life prediction can be made easily.
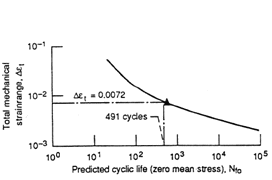
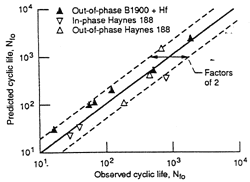
A sample TMF/TS-SRP life prediction curve is shown in Figure 7a. The assessment of the TMF life-prediction capability of the TMF/TS-SRP method is shown in Figure 7b. It is seen that the agreement is generally within the conventional factor of two associated with high-temperature fatigue life prediction in the nominally low-cycle fatigue regime.
 |
 |
| a | b |
Figure 7. (a) A sample TMF/TS-SRP life-prediction curve (zero mean stress condition) constructed for OP B1900+Hf. 483  t = 0.72%, observed life = 546 cycles, and predicted life = 491 cycles. (b) An assessment of TMF life-prediction capability of the TMF/TS-SRP method for two high-temperature aerospace superalloys.14 t = 0.72%, observed life = 546 cycles, and predicted life = 491 cycles. (b) An assessment of TMF life-prediction capability of the TMF/TS-SRP method for two high-temperature aerospace superalloys.14 |
|
A set of damage-curve relations is proposed for the modeling of damage accumulation according to each of the four fundamental deformation and damage modes given in SRP
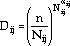 |
(55) |
where  ij, i,j = p,c may be considered as material-dependent parameters, and the damage variable, D, possesses a range of 0 (undamaged condition) to 1 (failure) over the domain of the life fraction n/Nij of 0 to 1.
ij, i,j = p,c may be considered as material-dependent parameters, and the damage variable, D, possesses a range of 0 (undamaged condition) to 1 (failure) over the domain of the life fraction n/Nij of 0 to 1.
When multiple damage modes are operative, an additional set of damage coupling relations is required,
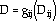 |
(56) |
where the functions, gij, i,j = p,c [where gpp(Dpp)  Dpp] must be determined by experiments.
Dpp] must be determined by experiments.
The coupling relations recognize that what is considered as damage in one context cannot be necessarily regarded as damage in another (e.g., pp-type cycling is associated with transgranular, classical fatigue-type damage, while cp-type cycling is associated with intergranular, creep-type damage). However, the coupling relations do imply that the damage state is relatable. The coupling relations provide a mapping or correspondence between damage modes.
To model the more general problem wherein multiple damage modes may be present within a single cycle, one additional relationship must be established—a description of how the various damaging contributions may be synthesized to provide a means of assessing the cumulative damage contribution
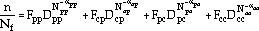 |
(57) |
This equation describes the cumulative damage behavior of a complex cycle (with life Nf) as life fraction, expressed in terms of the four damage variables, Dpp, Dcp, Dpc, and Dcc. Note that in general, the coupling relations must be invoked to recast Equation 57 in terms of one effective damage variable, D.
The model can be readily extended to treat the case of TMF through the use of the bithermal fatigue approximation to TMF. To address TMF, the life relations, damage-curve equations, and damage-coupling relations can be directly replaced by bithermal counterparts. Experiments consisting of two-level loadings of TMF (both IP and OP) followed by isothermal fatigue to failure were conducted on 316 stainless steel. It was found that the model gave good predictions for the OP two-level tests and provided reasonable bounds for the IP two-level tests.
An effective J-integral was developed for TMF crack-life prediction. The effective J-integral is an empirical strain-energy-density crack growth parameter and is not a rigorous fracture mechanics parameter.
The developed effective J-integral fracture mechanics TMF model is summarized as
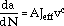 |
(58) |
where a is the crack depth, da/dN is the crack-growth rate, Jeff is the effective J-integral (an empirical strain-energy-density fracture mechanics parameter), A and c are material constants, and
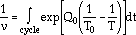 |
(59) |
where Q0 and T0 are material constants, T is the absolute temperature, and dt is the time increment.
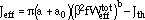 |
(60) |
where a0 is the initial material defect size (material constant), b is a material constant,  is the crack-boundary-correction factor, and Jth is the threshold J-integral that may be constant or temperature-dependent. For the latter, a good empirical temperature-dependent formula of Jth is
is the crack-boundary-correction factor, and Jth is the threshold J-integral that may be constant or temperature-dependent. For the latter, a good empirical temperature-dependent formula of Jth is
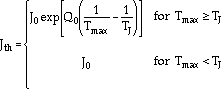 |
(61) |
where J0 is a constant and TJ is the temperature at which time-dependent deformation (creep) becomes significant in monotonic tensile tests.
Where f is a crystallographic strain-energy-correction factor,
 |
(62) |
where f<111> is a factor that resolves  max into the maximum normal octahedral slip plane stress, Emax is the elastic modulus in the
max into the maximum normal octahedral slip plane stress, Emax is the elastic modulus in the  max direction and at the
max direction and at the  max temperature, E<111> is elastic modulus in the <111> crystal direction and at the
max temperature, E<111> is elastic modulus in the <111> crystal direction and at the  max temperature, and
max temperature, and 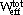 is the effective total strain-energy density.
is the effective total strain-energy density.
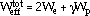 |
(63) |
where 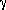 is the material constant, and We is the elastic strain-energy density
is the material constant, and We is the elastic strain-energy density
 |
(64) |
where m = 1 if  min > 0 and m = 0 if
min > 0 and m = 0 if  min
min 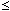 0.
0.
Wp is the plastic strain energy density:
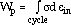 |
(65) |
where  > 0,
> 0,  is the stress,
is the stress,  max is the maximum stress,
max is the maximum stress,  min is the minimum stress of a cycle in which
min is the minimum stress of a cycle in which  max occurs, and d
max occurs, and d in is the inelastic strain increment.
in is the inelastic strain increment.
This TMF model's material constants are determined from a combination of uniaxial TMF and oxidation tests and by applying a nonlinear least-squares-regression analysis. Stresses were obtained from a nonlinear finite-element analysis of a TMF specimen strain-temperature history. Nonlinear stress-strain behavior was predicted using unified viscoplastic constitutive models.
The TMF life-model formulation is limited to transgranular cracking. The model can capture many TMF cracking effects, such as coating thickness, single-crystal anisotropy, cycle wave shape, dwell, and thermal exposure. TMF life predictions based on the modified effective J-integral model were in good agreement with observed uniaxial TMF specimen lives.
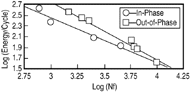 |
| Figure 8. Hysteretic energy life curves for a 316 stainless steel subjected to TMF tests in the temperature range of 399-621°C.21 |
The model developed for gas-turbine blades in electric power generation is based upon the parameters of strain range, strain amplitude ratio, and dwell time. This combination of parameters is intuitively reasonable, since the strain-amplitude ratio can account for mean strain effects, and the dwell time can consider environmental and mean stress effects caused by steady-state stress relaxation, both of which can affect the fatigue life.
The general form of the model is
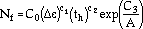 |
(66) |
where Nf is the fatigue life; A is the strain ratio, A =  amp/
amp/ mean (
mean ( amp =
amp = ,
 mean =
mean = , where all strains are mechanical strains);

 is the total strain range; th is the dwell time; and Ci (i = 0, 1, 2, and 3) is the empirical constant, determined from multiple regression of the TMF test data. In a test, the model adequately described the behavior of IN-738LC superalloy for the TMF-OP test conditions in the temperature range of 427-871°C.
is the total strain range; th is the dwell time; and Ci (i = 0, 1, 2, and 3) is the empirical constant, determined from multiple regression of the TMF test data. In a test, the model adequately described the behavior of IN-738LC superalloy for the TMF-OP test conditions in the temperature range of 427-871°C.
When the TMF model was used to predict the fatigue life of the in-service gas turbine blades, which may experience the different cycle types, a linear damage rule was used to account for the different cycle types
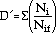 |
(67) |
where the damage ratio, D', was assumed to be one at 100% life consumed. Ni is the number of cycles of straining-type i, and Nif is the number of cycles to failure of type i.
Zamrik and colleagues have used the hysteretic-energy method to characterize the TMF behavior of type 316 stainless steel.21 From the stabilized mid-life hysteresis loop, the energy per volume cycle or density can be calculated and fit to the energy-life relation by
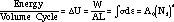 |
(68) |
where  U is the energy per volume cycle, W is the work or area of the hysteresis loop, A is the specimen cross-sectional area, L is the specimen gage length,
U is the energy per volume cycle, W is the work or area of the hysteresis loop, A is the specimen cross-sectional area, L is the specimen gage length,  is the stress, d
is the stress, d is the strain increment, A0 and a are constants, and Nf is the number of cycles to failure. The hysteretic energy versus life approach is illustrated in Figure 8. It can be observed that the TMF-IP hysteretic energy life line is lower than the TMF-OP line, which suggests more damage.
is the strain increment, A0 and a are constants, and Nf is the number of cycles to failure. The hysteretic energy versus life approach is illustrated in Figure 8. It can be observed that the TMF-IP hysteretic energy life line is lower than the TMF-OP line, which suggests more damage.
Kanasaki and colleagues have carried out axial-strain-controlled low-cycle fatigue tests of a carbon steel in oxygenated high-temperature water under TMF-IP and TMF-OP conditions.22 Based on the assumption that the fatigue damage increased in a linear proportion to the increment of strain during cycling, a fatigue-life prediction method was proposed.
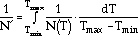 |
(69) |
where Tmax and Tmin are the maximum and minimum temperatures during TMF cycling, N(T) is the fatigue life in high-temperature water under isothermal conditions, and N' is fatigue life in high-temperature water under a TMF condition. For a carbon steel, STS410, under the conditions of DO = 1 ppm (in pure water containing 1 ppm oxygen) and  = 0.002% 1/s, N(T) was determined by the experiment
= 0.002% 1/s, N(T) was determined by the experiment
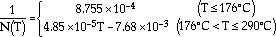 |
(70) |
A good relationship between the predicted N'pred and the experimental N'test was observed.
Damage modeling under thermomechanical cyclic loading is still at an early stage. TMF cycling is expected to introduce a multitude of cyclic deformation and damage mechanisms in superalloys, and the influence of these damage mechanisms on the material's fatigue-crack initiation and propagation behavior is not well understood at present. No generally accepted models of TMF fatigue-life prediction are currently available.
It is generally recognized that three dominant damage mechanisms (fatigue, oxidation, and creep damage) may occur during TMF loading conditions. Most proposed models of TMF fatigue-life prediction attempt to capture the effects of these damage mechanisms and their interactions. It is not certain if these dominant damage mechanisms operate simultaneously, or if some of them run and others become inoperative during a special TMF loading condition.
There are many factors affecting TMF lives, such as materials, maximum and minimum temperatures, temperature range, strain rate, strain range, strain-temperature phase, and dwell and cycle times. There is a difficulty in that the models quantitatively simulate the interaction of damage mechanisms; at present, views on how to deal with this problem differ. Based on this and the complexity of alloys systems, TMF-life-prediction models are generally time-consuming and expensive.
To develop effective TMF life-prediction approaches for superalloys, more experimental work and data collection are necessary on various materials placed under TMF loading conditions.
ABOUT THE AUTHORS
Changan Cai is an associate professor of engineering mechanics at GuiZhou University of Technology.
Peter K. Liaw is the Ivan Racheff Chair of Excellence and professor at the University of Tennessee.
Mingliang Ye is an associate professor of mining engineering with GuiZhou University of Technology.
Jie Yu is a professor of materials science and engineering with GuiZhou University of Technology.
For more information, contact P.K. Liaw, University of Tennessee at Knoxville, Department of Materials Science and Engineering, 427-B Dougherty Engineering Building, Knoxville, Tennessee 37996-2200; (423) 974-6356; fax (423) 974-4115; e-mail pliaw@utk.edu.
Direct questions about this or any other JOM page to jom@tms.org.
| Search | TMS Document Center | Subscriptions | Other Hypertext Articles | JOM | TMS OnLine |
|---|