 |
52 (7) (2000), pp. 39-42 |
|---|
Metallic Glasses: Overview
 |
52 (7) (2000), pp. 39-42 |
|---|
|
TABLE OF CONTENTS |
|---|
|
|
 |
|
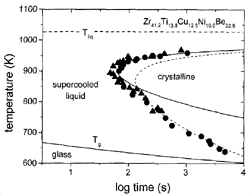
Figure 1. A time-temperature-transformation diagram for the primary crystallization of V1. Data obtained by electrostatic levitation (s)10 and processing in high-purity carbon crucibles (l)11 are included. Calculated times for a crystalline volume fraction of x = 10-4 , using Deff m h-1(solid line) and Deff m exp(–Q eff/kT) (dashed line). |
Bulk metallic glass-forming liquids are alloys with typically three to five metallic components that have a large atomic-size mismatch and a composition close to a deep eutectic. They are dense liquids with small free volumes and viscosities that are several orders of magnitude higher than in pure metals or previously known alloys. In addition, these melts are energetically closer to the crystalline state than other metallic melts due to their high packing density in conjunction with a tendency to develop short-range order. These factors lead to slow crystallization kinetics and high glass-forming ability. Crystallization kinetics is very complex, especially in the vicinity of the glass transition, due to the influence of phase separation and the decoupling of the diffusion constants of the different species.
In recent years new families of multicomponent glass-forming
alloys, such as La-Al-Ni,1
Zr-Ni-Al-Cu,2 Mg-Cu-Y,3
and Zr-Ti-Cu-Ni-Be,4 that
exhibit very good glass-forming ability have been discovered. These bulk metallic
glass (BMG) formers show high thermal stability of supercooled (undercooled)
liquid with respect to crystallization, enabling the study of the thermophysical
properties of metallic melts in the supercooled state and the exploration of
their properties and possible applications.5
Since their discovery in 1960 by Duwez and coworkers,6
much research has been devoted to the study of metallic glasses. Crucial contributions
were made by Turnbull, Chen, and collaborators,7,8
who showed, for example, that rapidly quenched Au-Si alloys exhibit a well-defined
calorimetric glass transition and viscosity. In the following years, thermophysical
properties like viscosity, relaxation, diffusion, and thermodynamics were explored
(e.g., Reference 9). However, the lack of thermal stability
in the supercooled liquid of metallic systems with respect to crystallization
did not allow studies deep into the supercooled liquid region, and most studies
were done below or in the vicinity of the glass transition region.
The novel BMG-forming liquids can now be studied in a much broader time and
temperature range. It is now even possible to measure time-temperature- transformation
(TTT) diagrams, such as the diagram shown for Zr41.2Ti13.8Cu10.0Ni12.5Be22.5
(V1) alloy in Figure 1. In this diagram,
the onset times for isothermal crystallization are plotted as a function of
temperature. The data were obtained by electrostatic levitation10
and crystallization in high-purity graphite crucibles.11
The diagram shows the typical “C” or nose shape and a minimum crystallization
time of 60 s at 895 K. For previously known glass-forming alloys, the times
were of the order of milliseconds, resulting in the need for rapid quenching
for vitrification. The TTT diagram of V1 reflects a very low critical cooling
rate of about 1 K/s, which is 5–6 orders of magnitude lower than in earlier
metallic glass-forming systems. The C shape is the result of the competition
between the increasing driving force for crystallization and the slowing of
kinetics (effective diffusivity) of the atoms. In simple liquids, atomic mobility
is connected to viscosity via the Stokes-Einstein relation.
If steady-state nucleation is assumed, the rate of nucleation is determined
by the product of a thermodynamic contribution and a kinetic contribution as
| Is = A·Deff exp(–DG*/kT) |
(1)
|
The driving force for crystallization is approximated by the
Gibbs free energy difference between supercooled liquid and crystal, DG.
Strictly speaking, DG is the driving force for a
polymorphic transformation (without a composition change) and a lower bound
for the driving force for transformations with composition change. Models for
the Gibbs free energy of metallic liquids have been developed by Turnbull,12
Thompson and Spaepen,13
and others.14,15
The thermodynamics of undercooled metallic liquids with respect to the crystal
have also been incorporated in calculation of phase diagrams (CALPHAD) calculations.16
An experimental assessment of the Gibbs free energy difference between liquid
and solid requires the determination of fusion heat and the difference in the
specific heat capacity, Dcp(T),
between supercooled liquid and crystal.
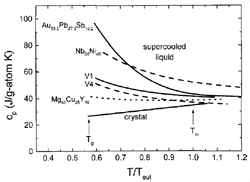
Figure 2 shows examples
of the specific heat capacity, cp, of several
glass-forming alloys as a function of temperature in the supercooled liquid
state. The temperature axis is normalized to the melting temperature of the
respective alloy. With the exception of the cp
of Nb-Ni, which was calculated by the CALPHAD method,17
all curves are based on experimental results. The cp
of the liquid at the melting temperature is higher than that of the crystalline
state and increases with undercooling even further. However, for the good BMG
formers (V1,19 Zr46.75Ti8.25Cu7.5Ni10Be27.5
[V2], and Mg-Cu-Y20), the curves are much
shallower than the other two alloys, which are materials with less favorable
glass-forming ability. This is due to the strong glassy nature of BMG liquids,
leading to a slower change in the configurations of the system as the glass
transition is approached.
|
|
|
|
 |
 |
|
|
Figure 2. Specific heat capacities in the supercooled liquid for several alloys normalized to the eutectic temperature, Teut . Data on Nb-Ni is taken from Reference 17; data on Au-Pb-Sb is from Reference 18. For the other data, see References 19 and 20. Good BMGs show a shallow cp curve that is indicative for strong liquid behavior. |
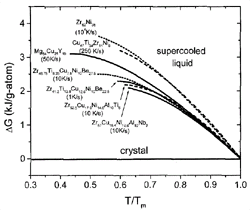
Figure 3. The difference in Gibbs free energy between the liquid and the crystalline state for glass-forming liquids. The data on Zr-Ni are taken from CALPHAD calculations.24 For the other alloys, see References 19, 20, and 23. The critical cooling rates for the alloys are indicated in the plot. |
|
|
|
|
The Gibbs free energy of the undercooled liquid with respect
to the crystal, DG1–x
(T), can be calculated by integrating the specific heat capacity difference
between supercooled liquid and crystal and taking into account the fusion heat.
For example, this has been done for Pd-Ni-P,21
Pd-Ni-Cu-P,22 Zr-Ti-Cu-Ni-Be,19
Mg-Cu-Y,20 and Cu-Ti-Zr-Ni.23
In Figure 3, the Gibbs free energy difference
for a selection of glass-forming systems is plotted as a function of undercooling.
All temperatures are normalized to the melting temperature of the respective
alloy. The alloys show different critical cooling rates between 1 K/s for the
pentary V1 and about 104 K/s for the binary
Zr62Ni38.
The glass formers with the lowest critical cooling rates have smaller Gibbs
free energy differences than do the glass formers with high critical cooling
rates.
The driving force for crystallization decreases with increasing BMG forming
ability. This originates mainly from the smaller entropies of fusion found in
the BMG system, since the fusion entropy determines the slope of the free-energy
curve at the melting point. A low value of entropy indicates a small free volume
and a tendency to develop short-range order at the melting point and in the
supercooled liquid. In fact, it was shown for V1 that the free volume at the
melting point is only one percent.11,25
These findings are consistent with the fact that BMG formers are very viscous
liquids at the melting point and upon undercooling.
Besides thermodynamic considerations, viscosity is the kinetic key parameter
that determines the nucleation and growth of crystals in the moderately undercooled
liquid (Equation 1). Viscosities of amorphous alloys have
been previously measured (e.g., by Chen and Turnbull7
and Spaepen and coworkers26,27).
The viscosities were determined in the glass-transition region, but crystallization
did not allow measurements of the equilibrium viscosity below 109
Pa · s or for times long enough to eliminate relaxation effects.
|
|
 |
|
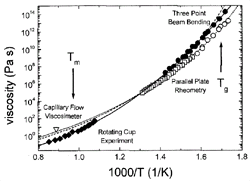
Figure 4. Viscosity data of V1 (solid symbols) and V4 (open symbols) measured by various methods. Fits to the data were obtained using the VFT equation (dashed curve: V1; dotted curve: V4). The data on V1 were additionally fitted using the modified free volume model by Cohen and Grest 32(solid curve). See References 11 and 28–30 for details. |
 |
|
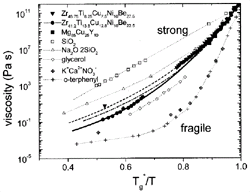
Figure 5. An Angell plot comparing the viscosities of different types of glass-forming liquids. The plot shows that V1, V4, and Mg-Cu-Y are relatively strong liquids. See References 11, 20, 29, and 30 for discussion. The data on the nonmetallic liquids are taken from Reference 31. |
Viscosity can be measured in bulk glass-forming systems in a much larger temperature
and time range than before. Figure 4
shows the viscosities for V1 and V4 in an Ahrrenius plot, obtained by different
methods (see References 11, 28–30
for details). The data cover 15 orders of magnitude, with the exception of the
temperature range where the crystallization nose in the TTT diagram (Figure
1) is observed. All equilibrium viscosity data measured in the supercooled
liquid can be described well with the Vogel-Fulcher-Tammann (VFT) relation
| h = h0 ·exp[D* ·T0/(T – T0)] |
(2)
|
Diffusion in the glassy state has previously been studied (e.g., Faupel and
coworkers41,42);
in the last five years, progress has been made to understand diffusion in the
glass-transition region and above. Particular attention has been paid to V1
and V4. Beginning with work by Geyer et al.43
on beryllium, the mobilities of other species in the glass-transition region
have been explored. Mehrer, Macht, and coworkers have conducted tracer-diffusion
studies on a variety of elements, such as cobalt, nickel, and aluminum.44,45
In addition, the isotope effect of cobalt in V4 has been measured, indicating
collective hopping.46
For temperatures below the glass transition, the differences in diffusivity
between the smallest and the largest atoms are up to five orders of magnitude.
This fact was known prior and has been studied extensively in connection with
solid-state amorphization in binary metallic glass formers.47,48
However, the glass-transition region and the supercooled liquid had not been
accessible in the past due to crystallization.
For the small beryllium atoms, pronounced changes in apparent activation energies
for diffusion were found in the glass transition region,43,49
which were attributed to a crossover from solid-like hopping at low temperature
to a cooperative shearing at high temperatures. The latter process is connected
to the viscosity and structural relaxation time of the material. Tang et al.
observed the hopping times of beryllium in the glass transition region directly
by NMR experiments.50,51
The fact that the glass transition temperature is a kinetic temperature makes
the design and the interpretation of experiments that probe atomic motion difficult.
The time scale on which a property is observed determines whether the material
is considered a supercooled liquid or a glassy solid. This has prompted continual
debates and further experiments.
One interesting fact is that the apparent activation energies for diffusion
of the different species increase monotonously with atomic size and the temperature
dependence of the diffusion for the large atoms such as aluminum (comparable
to zirconium) approaches the temperature dependence of the equilibrium viscosity.
Masuhr et al.11 compared
an overall (internal) relaxation time
| th = h/Gh |
| tD,I = l2/(6Di) |
|
|
 |
|
Figure 6. Structural relaxation times from viscosity are compared with the relaxation times for atomic diffusion, which have been determined from intrinsic diffusion constants of nickel,44 aluminum,45 and cobalt.45 |
These times are calculated from the measured viscosities and diffusivities,
respectively (Figure 6). Around 600 K,
the diffusivities of, for example, aluminum and nickel differ by three orders
of magnitude, while they show a tendency to merge at higher temperatures. The
temperature dependence of aluminum diffusion is similar to that of viscosity
tD,Al @
th/14 (dashed curve).
The proportionality factor implies that the mean displacement of an aluminum
atom in the supercooled liquid during a typical relaxation time is roughly four
interatomic diameters.
The smaller atoms show a significantly smaller absolute value of tD,
indicating that the mobility of the small atoms at low temperature is decoupled
from the relaxation kinetics given by viscosity. However, at high temperatures
a crossover is expected. At low temperatures, the atoms predominantly move by
atomic hopping because the motion due to cooperative shearing is several orders
of magnitude slower, as indicated by the structural relaxation time (Figure
6). Close to the crossover, the time scale for shear becomes comparable
to the hopping time, and the liquid-like motion is predominant. When a melt
is undercooled, each species experiences a different (glass) transition range
below which it moves in a solid-like environment.
 |
(3)
|
I thank W.L. Johnson for inspiration and continuing support and all his former and present group members at Caltech. My special thanks go to A. Masuhr, E. Bakke, T.A. Waniuk, W. Lui, and J. Schroers. My memories are with my late friend and fellow researcher at Caltech and JPL, Y.J. Kim. This work was supported by the U.S. Department of Energy (grant no. DEFG-03-86ER45242), the Alexander von Humboldt Foundation via the Feodor Lynen Program.
1. A. Inoue,
T. Zhang, and T. Masumoto, Mater.
Trans. JIM, 31 (1991), p. 425.
2. T. Zhang, A. Inoue, and T.
Masumoto, Mater.
Trans. JIM, 32 (1991), p. 1005.
3. A. Inoue et al., Mater.
Trans. JIM, 32 (1991), p. 609.
4. A. Peker and W. L. Johnson,
Appl.
Phys. Lett., 63 (1993), p. 2342.
5. W.L. Johnson, MRS
Bull., 24 (1999), p. 42.
6. W. Klement, R. Willens, and
P. Duwez, Nature,
187 (1960), p. 869.
7. H.S. Chen and D. Turnbull,
J. Chem. Phys.,
48 (1968), p. 2560.
8. H.S. Chen and D. Turnbull,
Acta
Metall., 17 (1969), p. 1021.
9. R.W. Cahn, Mater. Sci.
Technol., vol 9, ed. R.W. Cahn, P. Haasen, and E. Kramer (Weinheim, Germany:
Wiley-VCH, 1991).
10. Y.J. Kim et al., Appl.
Phys Lett., 68 (1996), p. 1057.
11. A. Masuhr et al., Phys.
Rev. Lett., 82 (1999), p. 2290.
12. D. Turnbull, J.
Appl. Phys., 21 (1950), p. 1022.
13. C.V. Thompson and F. Spaepen,
Acta
Metall., 27 (1979), p. 1855.
14. K.S. Dubey and P. Ramachandrarao,
Acta
Metall., 32 (1984), p. 323.
15. L. Battezzati and E. Garrone,
Z. Metallkde., 75 (1984), p. 305.
16. R. Bormann and K. Zöltzer,
Phys. Stat. Sol., 131 (1992), p. 691.
17. R. Busch, unpublished.
18. M.C. Lee et al., Mater.
Sci. Eng., 89 (1988), p. 301.
19. R. Busch, Y.J. Kim, and
W.L. Johnson, J. Appl.
Phys., 77 (1995), p. 4039.
20. R. Busch, W. Liu, and W.L.
Johnson, J. Appl. Phys.,
83 (1998), p. 4134.
21. G. Wilde et al., Appl.
Phys. Lett., 65 (1994), p. 397.
22. I.R. Lu et al., J. Non-Cryst.
Solids, 252 (1999), p. 577.
23. S.C. Glade et al., J.
Appl. Phys., 87 (2000), p. 7242.
24. F. Gärtner, private communication.
25. K. Ohsaka et al., Appl.
Phys. Lett., 70 (1997), p. 726.
26. S.S. Tsao and F. Spaepen,
Acta
Metall., 33 (1985), p. 1355.
27. C.A. Volkert and F. Spaepen,
Acta
Metall., 37 (1989), p. 1355.
28. E. Bakke, R. Busch, and
W.L. Johnson, Appl.
Phys. Lett., 67 (1995), p. 3260.
29. R. Busch, E. Bakke, and
W.L. Johnson, Acta
Mater., 46 (1998), p. 4725.
30. T.A. Waniuk et al., Acta
Mater., 46 (1998), p. 5229.
31. C.A. Angell, Science,
267 (1995), p. 1924.
32 G.S. Grest and M.H. Cohen,
Adv. Chem. Phys., 48 (1981), p. 455.
33. C.A. Angell, B.E. Richards,
and V. Velikov, J.
Phys.: Condens. Matter., 11 (1999), p. A75.
34. A. Meyer et al., Phys.
Rev. Lett., 80 (1998), p. 4454.
35. A. Meyer, R. Busch, and
H. Schober, Phys. Rev. Lett.,
85 (1999), p. 5027.
36. M. Weiss, M. Moske, and
K. Samwer, Appl.
Phys. Lett., 69 (1996), p. 3200.
37. K. Samwer, R. Busch, and
W.L. Johnson, Phys. Rev. Lett.,
82 (1999), p. 580.
38. M.K. Miller et al., J.
de Physique IV, 6 (C5) (1996), p. 217.
39. R. Busch et al., Appl.
Phys. Lett., 67 (1995), p. 1544.
40. S. Schneider, P. Thiyagarajan,
and W.L. Johnson, Appl.
Phys. Lett., 68 (1996), p. 493.
41. F. Faupel, P.W. Hüppe,
and K. Rätzke, Phys. Rev.
Lett., 65 (1990), p. 1219.
42. K. Rätzke, P.W. Hüppe,
and F. Faupel, Phys. Rev.
Lett., 68 (1992), p. 2347.
43. U. Geyer et al., Phys.
Rev. Lett., 75 (1995), p. 2364.
44. F. Wenwer et al., Defect
and Diffusion Forum, 143-147 (1997), p. 831.
45. E. Budke et al., Defect
and Diffusion Forum, 143-147 (1997), p. 825.
46. H. Ehmler et al., Phys.
Rev. Lett., 80 (1998), p. 4919.
47. W.L. Johnson, Prog.
Mat. Sci., 30 (1986), p. 81.
48. A.L. Greer, N. Karpe, and
J. Bottiger, J.
Alloys and Compounds, 194 (1993), p. 199.
49. U. Geyer et al., Appl.
Phys. Lett., 69 (1996), p. 2492.
50. X.P. Tang et al., Phys.
Rev. Lett., 81 (1998), p. 5358.
51. X.P. Tang et al., Nature,
402 (1999), p. 160.
52. R. Busch et al., Appl.
Phys. Lett., 67 (1996), p. 1544.
53. S. Schneider, P. Thiyagarajan,
and W.L. Johnson, Appl.
Phys. Lett., 68 (1996), p. 493.
54. W.H. Wang et al., Appl.
Phys. Lett., 71 (1997), p. 1053.
55. W.H. Wang, Q. Wei, and
S. Friedrich, Phys. Rev. B,
57 (1998), p. 8211.
56. J. Schroers et al., Phys.
Rev. B, 60 (1999), p. 11855.
57. J. Schroers et al., Appl.
Phys. Lett., 76 (2000), p. 2343.
58. K.F. Kelton, Philos.
Mag. Lett., 77 (1997), p. 337.
Ralf Busch is with the Department of Mechanical Engineering at Oregon State University.
For more information, contact R. Busch, Oregon State University,
Department of Mechanical Engineering, Rogers Hall 204, Corvallis, Oregon 97331;
(541) 737-2648; fax (541) 737-2600; e-mail ralf.busch@orst.edu.
Direct questions about this or any other JOM page to jom@tms.org.
| If you would like to comment on the July
2000 issue of JOM,
simply complete the JOM on-line critique form |
|||||
|---|---|---|---|---|---|
| Search | TMS Document Center | Subscriptions | Other Hypertext Articles | JOM | TMS OnLine |