 |
http://www.tms.org/pubs/journals/JOM/9908/Ress/Ress-9908.html
|
 |
http://www.tms.org/pubs/journals/JOM/9908/Ress/Ress-9908.html
|
 |
|---|
| TABLE OF CONTENTS |
The literature is full of reports of lattice parameters and bond angles that are variable or imprecise for chemicals. This imprecision is a result of the analysis techniques used and the imprecision in the samples and measurement process. Research has shown that fuzzy logic is a unique tool for representing imprecision; this article extends fuzzy research into the area of molecular modeling.
 |
 |
| a | b |
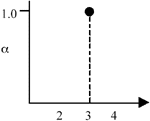
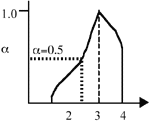
Figure 1. (a) The crisp set 3; (b) the fuzzy set  . . |
|
In normal set theory, an object is either a member of a set or not (i.e., there are only two states), and the set is often referred to as a crisp set. Fuzzy sets, on the other hand, have degrees of membership to that set. Thus, it is possible for an object to have partial membership in a set. This forms the basis of fuzzy-set theory. Figure 1 shows a comparison of a crisp set and a fuzzy set. Notice that the number two is not a member of the crisp set 3, but it is a member of the fuzzy set 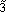 . The vertical axis is called the degree of membership (a) and is normalized such that a
. The vertical axis is called the degree of membership (a) and is normalized such that a  [0, 1]. For example, the number 2.5 has a degree of membership of 0.5 in the fuzzy set
[0, 1]. For example, the number 2.5 has a degree of membership of 0.5 in the fuzzy set 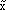 in Figure 1.
in Figure 1.
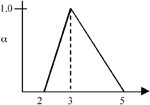 |
Figure 2. An example of triangular fuzzy numbers, where  = <2,3,5>. = <2,3,5>. |
The left and right spreads of a TFN are a common measure of the TFN's variability or imprecision. In Figure 2, the left spread is 3 – 2 = 1; the right spread is 5 – 3 = 2.
One reason why TFNs are well suited to modeling and design is because their arithmetic operators and functions are developed, which allow fast operation on equations. These arithmetic operators include the following examples, where the following TFNs are given:
 = <a1, a2, a3> and = <a1, a2, a3> and  = <b1, b2, b3> = <b1, b2, b3> |
and the following values are used for illustration:
 = <2, 4, 5> and = <2, 4, 5> and 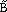 = <1, 2, 3> = <1, 2, 3> |
Addition
 =
=
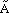 +
+
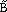 is defined as
is defined as
 = <c1, c2, c3> = <a1 + b1, a2 + b2, a3 + b3> = <c1, c2, c3> = <a1 + b1, a2 + b2, a3 + b3> |
(1) |
| e.g., |
Subtraction
 =
=
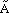 –
–
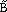 is defined as
is defined as
 = <c1, c2, c3> = <a1 – b3, a2 – b2, a3 – b1> = <c1, c2, c3> = <a1 – b3, a2 – b2, a3 – b1> |
(2) |
e.g.,  = <2 – 3, 4 – 2, 5 – 1> = <–1, 2, 4> = <2 – 3, 4 – 2, 5 – 1> = <–1, 2, 4> |
Multiplication
 =
=
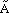 x
x
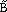 is defined as
is defined as
 = <c1, c2, c3> = <a1 x b1, a2 x b2, a3 x b3> = <c1, c2, c3> = <a1 x b1, a2 x b2, a3 x b3> |
(3) |
e.g.,  = <2 x 1, 4 x 2, 5 x 3> = <2, 8, 15> = <2 x 1, 4 x 2, 5 x 3> = <2, 8, 15> |
Division
 =
= 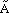 ÷
÷ 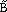 is defined as
is defined as
 = <c1, c2, c3> = <a1 ÷ b3, a2 ÷ b2, a3 ÷ b1> = <c1, c2, c3> = <a1 ÷ b3, a2 ÷ b2, a3 ÷ b1> |
(4) |
e.g.,  = <2 ÷ 3, 4 ÷ 2, 5 ÷ 1> = <0.667, 2, 5> = <2 ÷ 3, 4 ÷ 2, 5 ÷ 1> = <0.667, 2, 5> |
Exponentiation
 =
=
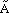 k (where k is the crisp scalar with, for example, a value of 0.5) is defined as
k (where k is the crisp scalar with, for example, a value of 0.5) is defined as
 = <c1, c2, c3> = <a1k, a2k, a3k> = <c1, c2, c3> = <a1k, a2k, a3k> |
(5) |
e.g.,  = <20.5, 40.5, 50.5> = <1.414, 2, 2.236> = <20.5, 40.5, 50.5> = <1.414, 2, 2.236> |
In addition to these five arithmetic operators, recent research into fuzzy trigonometric functions has produced fuzzy versions of the cosine, sine, tangent, cotangent, secant, and cosecant functions (plus their respective inverses) that work with TFNs and the above arithmetic operators.4 Together, the arithmetic operators and trigonometric functions enable the modeling of chemical compounds and the calculation of fuzzy bond lengths and fuzzy bond angles.
 |
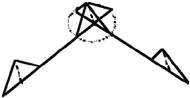
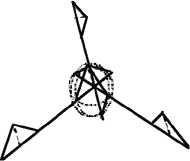
| Figure 3. A example of fuzzy lines where (top) point A is fixed, point B is fuzzy, and (bottom) point A is fuzzy, and point B is fuzzy. Also shown are values for the fuzzy endpoints. |
One solution is to take the average value, but that, in effect, creates a biased value with no retention of the variability of the data. Another approach is to create fuzzy lattice parameters and apply them to the Wyckoff coordinates. The fuzzy lattice parameters are created by searching the literature for experiments performed under the same conditions and then extracting the minimum, average, and maximum values for each lattice parameter—thus creating TFNs. The end result is a fuzzy unit cell, with fuzzy bond lengths and fuzzy bond angles, that incorporates the variability found in literature. However, two interesting phenomena arise in creating fuzzy unit cells—the concept of fuzzy lines and fuzzy vertices.
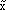 = <8, 10, 12>Å), the endpoints must be determined to model a fuzzy unit cell. Two possible answers are shown in Figure 3.
= <8, 10, 12>Å), the endpoints must be determined to model a fuzzy unit cell. Two possible answers are shown in Figure 3.
 |
| a |
 |
| b |
| Figure 4. The (a) 2-D and (b) 3-D fuzzy vertices. |
Using values extracted from literature,6–12 the fuzzy lattice parameters are
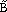 = <5.773, 5.781, 5.785> Å
= <5.773, 5.781, 5.785> Å
 = <11.550, 11.602, 11.642> Å
= <11.550, 11.602, 11.642> Å
and the anion displacement parameter is
 = <0.220, 0.230, 0.249>
= <0.220, 0.230, 0.249>
The "Fuzzy" Applets page also contains a Java applet for calculating the fuzzy density of a chalcopyrite compound. While most of the properties of chemical compounds have indirect relationships with the lattice parameters, density has a direct relationship. For example, if considering CuInSe2, the fuzzy lattice parameters can be used to calculate a fuzzy representation of the volume of the unit cell. From a standard periodic table of elements, the mass of copper, indium, and selenium is used to find the total mass of the fuzzy unit cell, which is 2.234 x 10–21 grams. As density is the ratio of mass over volume, the fuzzy density for CuInSe2 is <5.733, 5.761, 5.803> g/cm3. Thus, the density may be as low as 5.733 g/cm3 or as high as 5.803 g/cm3, but we would expect it to be nominally 5.761 g/cm3.
 = <3.870, 3.882, 3.890> Å
= <3.870, 3.882, 3.890> Å
 = <11.666, 11.687, 11.708> Å
= <11.666, 11.687, 11.708> Å
Using the fuzzy lattice parameters and the Wyckoff coordinates for the Pmmm space group,20 a fuzzy unit cell for the YBa2Cu3O7 compound was constructed (Figure 6, an animation).
| Table I. Selected Fuzzy Bond Angles and Lengths for CuInSe213 and YBa2Cu3O721 | |||||
|---|---|---|---|---|---|
| Compound | Bond Angles (°) | Crisp (°) | Bond Lengths (Å) | Crisp (Å) | |
| CuInSe2 | |||||
| Cu1-Se-Cu2 | <109.593, 113.999, 115.877> | 114.870 | -- | -- | |
| Cu1-Se-In1 | <106.269, 109.141, 111.512> | 108.902 | -- | -- | |
| Cu1-Se-In2 | <106.374, 109.421, 112.127> | 109.462 | -- | -- | |
| Cu2-Se-In1 | <106.405, 109.421, 112.175> | 109.462 | -- | -- | |
| Cu2-Se-In2 | <107.499, 109.141, 110.624> | 108.902 | -- | -- | |
| In1-Se-In2 | <103.127, 105.329, 109.073> | 104.760 | -- | -- | |
| Se-Cu1 | -- | -- | <2.390, 2.441, 2.527> | 2.4337 | |
| Se-Cu2 | -- | -- | <2.400, 2.441, 2.512> | 2.4337 | |
| Se-In1 | -- | -- | <2.488, 2.575, 2.632> | 2.5893 | |
| Se-In2 | -- | -- | <2.499, 2.575, 2.619> | 2.5893 | |
| YBa2Cu3O7 | |||||
| Cu(m)-O(m)-Cu(m) | <160.54, 164.29, 168.71> | 164.27 | -- | -- | |
| Cu(m)-O(m')-Cu(m) | <161.70, 163.89, 166.16> | 163.92 | -- | -- | |
| Cu(t)-O(t') | -- | -- | <1.919, 1.941, 1.959> | 1.942 | |
| Cu(t)-O(b) | -- | -- | <1.819, 1.833, 1.846> | 1.846 | |
| Cu(m)-O(b) | -- | -- | <2.291, 2.322, 2.354> | 2.298 | |
| Cu(m)-O(m) | -- | -- | <1.912, 1.933, 1.954> | 1.929 | |
| Cu(m)-O(m') | -- | -- | <1.947, 1.960, 1.974> | 1.961 | |
| Ba-O(t') | -- | -- | <2.870, 2.892, 2.914> | 2.876 | |
| Ba-O(m) | -- | -- | <2.958, 2.973, 2.989> | 2.982 | |
| Ba-O(m') | -- | -- | <2.944, 2.964, 2.985> | 2.959 | |
| Ba-O(b) | -- | -- | <2.727, 2.747, 2.767> | 2.741 | |
| Y-O(m) | -- | -- | <2.389, 2.408, 2.427> | 2.409 | |
| Y-O(m') | -- | -- | <2.389, 2.408, 2.427> | 2.385 | |
It is believed that this research is a necessary first step to representing the imprecision found in unit cells and will, hopefully, lead to a better understanding of chemical properties.
References
1. L.A. Zadeh, "Fuzzy Sets," Information and Control, 8 (3) (1965), pp. 338–353.
2. H-J. Zimmermann, Fuzzy Set Theory and Its Application, 2nd ed. (Boston, MA: Kluwer Academic Publications, 1991).
3. T.J. Ross, Fuzzy Logic with Engineering Applications (New York: McGraw-Hill, 1995).
4. D.A. Ress, "Development of Fuzzy Trigonometric Functions to Support Design and Manufacturing" (Dissertation thesis, Department of Industrial Engineering, North Carolina State University, 1999).
5. W.G. Wyckoff, Crystal Structure (New York: Wiley-Interscience Publishers, 1963).
6. J. E. Jaffe and A. Zunger, "Electronic Structure of the Ternary Chalcopyrite Semiconductors CuAlS2, CuGaS2, CuInS2, CuAlSe2, CuGaSe2, and CuInSe2," Physical Review B, 28 (10) (1983), 5822-5847.
7. P. Kistaiah and K.S. Satyanarayanamurthy, "Temperature Behaviour of the Tetragonal Distortion and Thermal Expansion of Gu-II-VI2 Chalcopyrite Semiconductors," J. Less Comm. Met., 105 (1985), pp. 37–54.
8. J.E. Jaffe and A. Zunger, "Theory of Band Gap Anomaly in ABC2 Chalcopyrite Semiconductors," Physical Review B, 29 (4) (1984), pp. 1882–1906.
9. H.Y. Ueng and H.L. Wang, "Defect Structure of the Nonstoichiometric Cu-I-III-VI2 Chalcopyrite Semiconductors,"Non-Stoichiometry in Semiconductors, ed. K.J. Bachmann, H.-L. Hwang, and C. Schwab (Netherlands: Elsevier Science Publishers B.V., 1992), pp. 69–79.
10. B.R. Pamplin, T. Kiyosawa, and K. Masumoto, "Ternary Chalcopyrite Compounds," Prog. Crystal. Growth Charact., 1 (1979), pp. 331–387.
11. J.L. Shay and J.H. Wernick, Ternary Chalcopyrite Semiconductors: Growth, Electronic Properties, and Applications (New York: Pergamon Press, 1975).
12. L.I. Berger and V.D. Prochukan, Ternary Diamond-Like Semiconductors (New York: Consultants Bureau, 1969).
13. K.S. Knight, "The Crystal Structure of CuInSe2 and CuInTe2," Materials Research Bulletin, 27 (1992), pp. 161–167.
14. M.A. Beno et al., 1987. "Structure of the Single-Phase High-Temperature Superconductor YBa2Cu3O7- ," Applied Physics Letters, 51 (1987), pp. 57–59.
," Applied Physics Letters, 51 (1987), pp. 57–59.
15. J.J. Capponi et al., "Structure of the 100K Superconductor Ba2YCu3O7 between (5÷300)K by Neutron Powder Diffraction," Europhys. Lett., 3 (12) (1987), pp. 1301–1307.
16. F. Beech et al., "Neutron Study of the Crystal Structure of the Superconductor Ba2YCu3O9-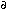 ," Physical Review B, 35 (16) (1987), pp. 8778–8781.
," Physical Review B, 35 (16) (1987), pp. 8778–8781.
17. J.E. Greedan, A.H. O'Reilly, and C.V. Stager, "Oxygen Ordering in the Crystal Structure of the 93-K Superconductor YBa2Cu3O7 Using Powder Neutron Diffraction at 298 and 79.5K," Physical Review B, 35 (16) (1987), pp. 8770–8773.
18. Y. LePage et al., "Room-Temperature Structure of the 90-K Bulk Superconductor YBa2Cu3O8-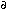 ," Physical Review B, 35 (13) (1987), pp. 7245–7248.
," Physical Review B, 35 (13) (1987), pp. 7245–7248.
19. T. Siegrist et al., "Crystal Structure of the High-Tc Superconductor Ba2YCu3O9-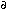 ," B, 35 (13) (1987), pp. 7137–7139.
," B, 35 (13) (1987), pp. 7137–7139.
20. C.P. Poole, Jr, T. Datta, and H.A. Farach, Copper Oxide Superconductors (New York: John Wiley & Sons, 1988).
21. P. Bordet et al., "Crystal Structure of Y0.9Ba2.1Cu3O9, a Compound Related to the High-Tc Superconductor YBa2Cu3O7," Nature, 327 (1987), pp. 687–689.
ABOUT THE AUTHOR
David A. Ress is with the Materials Process Design Branch of the Air Force Research Laboratory at Wright-Patterson Air Force Base.
For more information, contact D.A. Ress, Air Force Research Laboratory, MLMR, 2977 P Street, Suite 13, WPAFB, Ohio 45433-7746; e-mail 75112.444@compuserve.com.
Direct questions about this or any other JOM page to jom@tms.org.
| Search | TMS Document Center | Subscriptions | Other Hypertext Articles | JOM | TMS OnLine |
|---|