 | 48 (12) (1996), pp. 43-47. JOM is a publication of The Minerals, Metals & Materials Society |
|---|
 | 48 (12) (1996), pp. 43-47. JOM is a publication of The Minerals, Metals & Materials Society |
|---|
| CONTENTS |
|---|
Recent developments in modeling can eliminate much experimental laboratory work and can provide quick answers in a more cost-effective manner. This article presents a brief outline of technical cost modeling, a combination of physical modeling and cost modeling, which may be used to the mutual benefit of both the managerial decision makers and the R&D community within the materials processing field.
Nonetheless, it must be recognized that these decisions are also constrained by a host of scientific as well as technological boundaries. These physical constraints define the technical feasibility and business potential of a given project. Obvious to a scientist or an engineer, there are certain laws and/or relationships that must be obeyed, no matter how financially attractive it may be to violate them. The fact that matter and thermal energy must be conserved (i.e., they cannot be produced from "thin air") should be as instinctively obvious as the fallacy of chemically turning lead into gold.
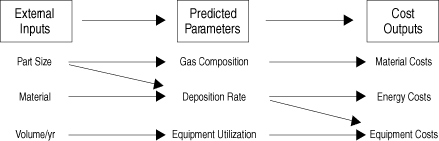 |
| Figure 1. The technical cost modeling methodology. |
Many more laws or relationships exist, and their manifestation tends to be much more subtle; typical examples include the rate at which specimens can be heated or cooled, the force or energy needed to deform or break materials, and the speed with which materials may be mixed or separated. Some of these laws are absolute, like Newton's Law of Motion, while others have a less well established or more tenuous basis. Suffice it to say that arbitrarily setting business performance goals without due cognizance of the underlying technical issues may be just as unrealistic as specifying an absolute level of profitability.
Traditionally, R&D tasks have been compartmentalized, especially in large companies, and widely separated from the groups responsible for business development. Generally, R&D groups paid little attention to manufacturability and cost, rendering much of the intellectually excellent (and, at times, very expensive) research quite remote from even the long-range goals of the business. Such disconnected research operations often fall prey to cost-cutting measures, the results of which are well documented. These developments are taking place even in the face of many key research innovations (e.g., the increased use of computers) that can eliminate much of the experimental laboratory work and can provide quick answers in a more cost-effective manner. The purpose of this article is to develop the theme that, using current experience and methodologies, the mathematical tools used for materials research and the techniques for cost estimation can be combined to benefit the managerial decision-making process and provide better focus for the research community.
| Table I. A Comparison of Various Casting Processes for the Production of Aluminum Auto Parts | ||||
|---|---|---|---|---|
| Main Characteristic | Casting GravityA | Low-Pressure Die CastingB | High-Pressure Die Casting (Pores Free)C | Squeeze CastingD |
| Pouring/Filling Method | Ladle | Air pressure through stalk | High-speed and high-pressure injection by hydraulic piston | Relatively low-speed and high-pressure injection |
| Filling Time (s) | 10-30 | 10-30 | 1 | 10 |
| Operating Pressure (atm.) | 1 | 1+(0.2-0.5) | 100-500 | 500-1,000 |
| Cycle Time (min.) | 5-10 | 5-10 | 1-2 | 2 |
| Die/Mold Temperature | High | High | Low | Low-medium |
| Dimensional Accuracy | + | ++ | +++ | +++ |
| Design Availability | +++ | ++ | + | + |
| Productivity | + | ++ | +++ | +++ |
| Quality | + | ++ | +-+++ | +++ |
| Cost | + | + | +++ | +++ |
| Machining Required | Many | Many | Few | Few |
| Main Parts (other than wheels) | Intake manifold, cylinder block and head, piston | Cylinder block, cylinder head, suspension, member | Cylinder block, oil pan, cylinder head cover, tranxile case | Piston, disk-brake caliper, power steering case, toe control hub, knuckle |
| AAluminum Casting Technology, 2nd ed., AFS, 1993. BASM Metals Handbook, vol. 15, Casting (Materials Park, OH: ASM, 1988). CCompany report of Japan Light Metals. DTechnical catalog from UBE Industries, Ltd. |
||||
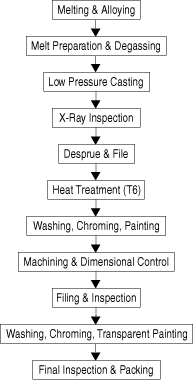 |
| Figure 2. A process flow diagram for the production of aluminum wheels by low-pressure casting. |
Technical cost modeling (TCM) is the label used to describe the marriage
of these two modeling disciplinesdescriptive cost models with predictive technical models. Schematically, the TCM methodology is illustrated in Figure 1. In a TCM, algorithms describing the kinetics, thermodynamics, and transport phenomena associated with a process are used to predict values such as the cycle time, power requirement, and materials consumption. In turn, these parameters are directly related to the costs of the materials, energy, and labor associated with the process. Thus, the inputs to these models may include temperatures, pressures, lengths, and areas, while the outputs will include equipment prices, piece costs, and fully accounted annualized business expenses. With this modeling approach, the cost of poorly understood processes can be estimated with some degree of certainty, and sensible technology development strategies for optimizing these processes can be devised.
APPLICATIONS
Both of the following examples of TCM applications were drawn from the materials production field and were explicitly product or process oriented. A particularly fruitful application of TCM may be found in addressing waste minimization and environmental issues in materials processing, which are receiving much closer attention at present as pressure demands that environmentally appropriate solutions also meet the criteria of cost effectiveness. TCM will be a critical tool in these endeavors.
|
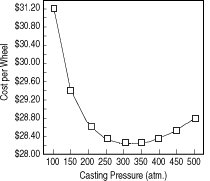
| Figure 3. Cost versus casting pressure as determined by the TCM for casting aluminum wheels. |
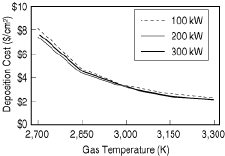 |
| Figure 4. Cost versus power and temperature as determined by the TCM for arcjet CVD diamond. Conditions: 1,000 W/mK thermal conductivity, 15.24 cm substrate diameter, 1 mm thickness. |
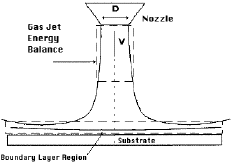 |
| Figure 5. The d.c. arcjet geometry used in the CVD process as assumed for simulations. Source: Goodwin, D.G., memo to Ibis Associates, June 1993. |
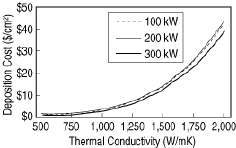 |
| Figure 6. Cost versus power and thermal conductivity with the d.c. arcjet technology as determined by the TCM. Conditions: 15.24 cm substrate diameter, 3,000 K gas temperature, 1 mm thickness. |
Aluminum components for automobiles such as engine blocks, cylinder heads, wheels, transmission casings, or brake calipers represent an important market, both for original equipment manufacturers and the aftermarket. These components are usually produced in foundries, which may or may not be closely tied to the automobile manufacturers themselves. At present, there are several technologies available for the production of these components, and the optimal choice depends on both the technological and the economic factors of a given process and/or material.4 The example of TCM presented here applies to the casting of aluminum wheels, but similar considerations can beapplied to the other components as well, although the specific technologies may, of course, differ.
Several technologies are available for the casting of aluminum wheels, including:
The use of TCM is ideal for optimizing the technology for this application by considering, in detail, the operation's characteristics mold filling, thermal history, solidification, and microstructural evolution together with all of the cost and production factors involved. With wheels or other products that are relatively new, a detailed modeling study is easily justified given the capital requirements associated with manufacturing this product. To illustrate the power of modeling, consider only the low-pressure die casting technology. The actual flow chart of the casting process is shown in Figure 2, which shows a sequence of batch operations, each requiring machinery, energy, time, and labor.
With a descriptive cost model, one could jump immediately from this flow sheet to a cost analysis and obtain information on the projected production costs. Indeed, such an analysis could be performed by an individual with no technical knowledge of the casting process. However, in doing so, the analyst will have to obtain the input parameters from outside sourceseither internal experts or, even difficult, outside suppliers. The analyst has not gained an understanding of the accuracy of the processing assumptions and, as a result, will have no calibration or independent evaluation to determine how good these numbers are.
With a mechanistic process model, one could examine the technical issues pertaining to the casting process, including how the metal is heated, how the mold is filled, how the molten metal solidifies, and under what conditions to expect defect formation. There are highly sophisticated mathematical process models available for such a purpose.5
By combining both types of analyses, a TCM is developed that generates results such as those shown in Figure 3. In this example, casting pressure is varied over a range of 100500 atm., and the effect of this change on wheel cost is observed. In the lower-pressure regime, increasing pressure reduces porosity and improves product yield. Higher pressures only increase the cost of the capital equipment required in the higher-pressure regime. An optimal process condition of 300 atm. is determined.
|
Mathematical Modeling A mathematical process model is a set of equations or mathematical formulae that describes or maps out the steps in a given process or unit operation.1 In most cases, these equations are solved or manipulated by computers, and the output of the model is an attractive color chart. For example, in the production of aluminum automotive components by casting, molten aluminum is poured into water- or air-cooled molds, where it solidifies to produce the primary shape of the part. In seeking to mathematically model such a process, we need to represent the way that molten metal flows, cools, and solidifies. Computer-generated plots may depict how the mold is filled, how temperatures change over time, how the melt solidifies, or under what conditions defects may form. This latter information (i.e., the conditions under which defects form) is of critical interest to the production manager. The issues of flow patterns, temperature profiles, and solidification rates may be regarded as superfluous except as they effect the problem of the defects. Once the information is successfully modeled, the process can be changed (e.g., the mold design, the superheat of the metal, the pouring rate, or the cooling arrangements) and the effect of these changes on defect generation can be examined. In the past, this process was done by trial and error. Presently, this goal can be reached faster and in a much more cost-effective and useful manner by using the computer model.
Model Types
Mechanistic models are based on the fundamental laws of chemistry and physics such as the description of the equilibrium composition between phases, the rates of chemical reactions, the laws of heat transfer, fluid flow, and magnetism. Generally, these laws are expressed in terms of quite complex differential equations (e.g., the Navier-Stokes equations, Fourier's equation, or Maxwell's equations). Until recently, these relationships were of academic interest only, however, with the rapid evolution of computational hardware and software, an experienced technical person can generate solutions to these problems in a relatively short time. Structural models such as a finite-element model that are used to simulate the mechanical properties or response of a given structure to a set of static, dynamic, or thermal loads are also included in this category. The third group of models correspond to stochastic models or empirically obtained relationships. Such models can be very useful, especially for traditional industries (i.e., steel, glass, cement, and aluminum) where there is a substantial experience base and much information on operational practice. These empirical models or databases are helpful for the control and optimization of existing processes, but have limited use in new process development.
Model Development
Applications
(Just consider the level of sophistication needed to operate a guided missile, a smart bomb, or a laser-guided armament.) However, in order to deploy the systems effectively, one needs a quantitative description of the system that may interface with the controller. A suitably adapted (simplified) mathematical model is ideal for this purpose.
The Shortcoming
Cost Models3 Cost remained relatively simple throughout the time span between the development of currency-based economies and the Industrial Revolution. It seems reasonable to speculate that labor and raw materials costs dominated most aspects of the world's economy in this timeframe, and managing these costs required little more than an abacus. Capital equipment, energy, land space, process yields, and the time value of money are aspects of modern cost accounting that were, for the most part, insignificant in early societies. In these societies, cost was simply the sum of the materials and labor required to produce a good or service. With the Industrial Revolution, cost accounting and estimation became significantly more complicated and has continued to grow in complexity to this day. In many manufacturing businesses, capital costs are more important than materials and labor, and with this change, process parameters such as throughput, yield, and the cost of capital became significant. As manufacturing processes became more and more automated, energy costs gained an important role in many processes. Because of these complexities, accounting for cost as well as predicting or estimating costs became specialties unto themselves. In the face of this evolution, the practices of cost estimation lagged behind. The default cost-estimation procedure, still followed almost universally by large and small businesses alike, is to estimate cost according to Equation A.
With the development of computer spreadsheets, descriptive cost modeling became straightforward. Instead of treating cost as a simple labor-based equation, it became relatively easy to define cost equations capturing multiple cost factors and the interrelationships among these. For instance, Equations B and C comprise an approach for estimating direct labor and electricity costs. Furthermore, these equations capture one of the physical linkages (C-Time) existing between these two cost factors.
|
CVD Diamond6-8
Alternatively, consider the emerging technology of chemical vapor deposition (CVD) diamond manufacturing. Worldwide recognition of the process only dates back to the early 1980s; depending on one's metric of measurement, the first commercial production of CVD diamond occurred sometime around 1990 or else is still to come. This technology is still emerging, yet a great deal has been learned regarding its economics through the application of TCM. For instance, Figure 4 shows the sensitivity of cost to changes in reactor gas temperature. While this analysis does make a leap of faith in assuming that these temperatures are technically feasible, it clearly points out the value of high-temperature CVD reactors. In essence, this analysis bridges the gap between scientific and economic information. Furthermore, it sets a clear, recognizable, engineering goal.
The graph shown in Figure 4 could not be solely developed through traditional cost or process modeling approaches; a brief review of the theory and analysis underpinning this graph is illustrative of the TCM process.
The direct current (d.c.) arcjet technology for making CVD diamond is depicted in Figure 5. In this process, methane or some other carbon-bearing gas is subjected to an extremely high temperature in the presence of hydrogen gas. The carbon from the carbon-bearing gas is deposited on a substrate in the form of diamond. In the case of the d.c. arcjet technology, an electric arc discharge is used as the source of energy. Hydrogen, the other gaseous ingredient, plays a critical role in the process. Atomistically, the process proceeds as follows: the energy of the d.c. arc is sufficient to break a significant fraction of the molecular hydrogen gas into atomic hydrogen. Atomic hydrogenthe active ingredient in the processattacks the substrate onto which the diamond is being deposited, creating active bonding sites. Carbon containing gas molecules, present in the reactor, bond to these sites. Finally, atomic hydrogen etches away all unwanted, non-diamond carbon atoms from the surface, leaving only a uniform diamond film.
From this description, it is clear that atomic hydrogen is an important ingredient in the process. Ultimately, predicting the cost of the process depends, fundamentally, on one's ability to predict the quantity of atomic hydrogen being transported to the substrate.
From the science of thermodynamics, it is possible to estimate the amount of atomic hydrogen present in the bulk gas stream, given the amount of energy flowing into the electric arc. Mass transport theory provides a basis for estimating the rate at which atomic hydrogen reaches the substrate. These technical disciplines provide the basis for estimating the diamond deposition rate as well as the process energy consumption, and ultimately, even the direct labor cost of the process.
With a scientifically grounded cost model in hand, it now becomes possible to examine the impact of a variety of technical parameters on the expected cost of the diamond produced. In a series of virtual experiments, the influence of power, pressure, temperature, and gas composition can be examined. Optimal production scenarios can be devised without the expense of running exhaustive, expensive, and time-consuming experiments. Instead, a much smaller set of experiments can be run to verify the model.
The CVD diamond film technology is being investigated by such companies as Norton, General Electric, DeBeers, Raytheon, 3M, and Lockheed. More than a technical curiosity, these corporations are viewing CVD diamond as a commercial business venture. There are many potential markets and applications that could, in principal, utilize the physical properties intrinsic to diamond. For instance, electronic substrates may one day be made of diamond, taking advantage of the unparalleled thermal conductivity inherent to diamond. The high thermal conductivity of diamond allows it to dissipate heat rapidly, permitting high-powered electronic devices to be packed more densely on a given circuit board and allowing these devices to be operated at higher frequencies where more power must be dissipated.
An atomistic model has been developed that allows the prediction of thermal conductivity from the composition of the gases at the substrate in the CVD reactor. In particular, as the ratio of atomic hydrogen to carbon-bearing gas increases, so does the thermal conductivity of the resultant diamond film. With this knowledge, it is now possible to predict the relationship between the cost of CVD diamond and its thermal conductivity. An example of this relationship is shown in Figure 6. As suspected, producing films that have higher thermal conductivity comes at a significant expense. The knowledge of this relationship, coupled with an understanding of the needs of a given market or application, facilitates better product pricing and positioning during market development.
CONCLUSION
The casting of aluminum wheels, drawn from tonnage materials processing, and the CVD diamond deposition, drawn from the high-technology field, provide excellent illustrations of the power of combining mathematical process modeling with cost modeling.
The CVD diamond example, in which properties, process, and cost are all linked in a single-model framework, suggests the level to which new technology-based business development can be steered by simulation modeling. Through modeling, business developers are able to design optimized products and optimized manufacturing processes without resorting to extensive, lengthy, process development experiments. Of course, the state of the art in an integrated TCM does not yet fully permit such practices, but with time and additional resources, there will likely come a day when such practices are commonplace.
It is a truism that awareness of the cost implications is critical in all phases of an R&D and process-implementation operation. At the same time, economic decisions cannot be made rationally in the absence of accurate and reliable technical information. Traditionally, in the materials processing industries there has been very little contact between the financial (cost) experts and those engaged in technology.
The critical point of this article is that the coordination of technological and cost factors must be borne in mind throughout a given project. Both cost and technology considerations have to be incorporated in the decision-making process at the process selection and initiation stage. This combined approach appears to be the most effective when cost and technology considerations are fully integrated, as illustrated in the wheel casting and CVD examples presented, where dollars, pressures, and/or production rates appeared in the same figures.
References
1. J. Szekely and G. Trapaga, "Some Perspectives on the Mathematical Modelling of Materials Processing Operations," Modelling and Simulation in Materials Science and Engineering (1994), pp. 809828.
2. J. Szekely, J. Evans, and J.K. Brimacombe, The Mathematical and Physical Modeling of Primary Metals Processing Operations (New York: John Wiley & Sons, 1988).
3. J. Busch, "Cost Modeling as a Technical Management Tool," Research Technology Management (1993).
4. J. Szekely, G. Trapaga, and N. Saluja, "An Automated Aluminum Foundry for the Production of Automotive Castings," A Feasibility Study (Washington, D.C.: U.S. Trade Development Agency, July 1993).
5. Y. Otsuka, G. Trapaga, and J. Szekely, "Optimal Casting Design by Application of Mold Filling and Solidification Simulation," Light Metals 1994, ed. U. Mannweiler (Warrendale, PA: TMS, 1994), pp. 897905.
6. D.J. Goodwin, "Scaling Laws for Diamond Chemical Vapor Deposition," Journal of Applied Physics, 74, pp. 68886906.
7. J.P. Dismukes et al., "Economic Assessment of CVD Diamond Synthesis Technologies," Proceedings from 1st Int'l. Conference on the Application of Diamond Films and Related Materials., ed. Y. Tzeng et al. (New York: Elsevier Science Publishers, 1991).
8. A. Singer, "Managing New Technologies with Technical Cost Modeling: CVD Diamond" (NEPCON West 1994, Anaheim, CA, February 1994).
For more information, contact G. Trapaga, Massachusetts Institute of Technology, Room 8-135, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139-4307; (617) 253-3150; fax (617) 253-8124; or J. Busch, IBIS Associates, 55 Williams Street, Wellesley, Massachusetts 02181; (617) 239-0666.
Direct questions about this or any other JOM page to jom@tms.org.
| Search | TMS Document Center | Subscriptions | Other Hypertext Articles | JOM | TMS OnLine |
|---|