|
|
|
 |
http://www.tms.org/pubs/journals/JOM/0001/Asthana/Asthana-0001.html
|
Functional Coatings: Overview
|
|
|
 |
http://www.tms.org/pubs/journals/JOM/0001/Asthana/Asthana-0001.html
|
Functional Coatings: Overview
The fundamental phenomena underlying various coating technologies include wetting, spreading, interface evolution, and adhesion. This article reviews the status of wettability and interfacial phenomena in high-temperature solid-liquid couples commonly employed in the coating and joining technologies.
The deposition of a coating on a solid generates new interfaces between dissimilar materials and involves considerations of wettability, spreading, interface evolution, and adhesion. The wettability of a solid by a liquid is characterized in terms of the angle of contact that the liquid makes on the solid.1,2 The contact angle, q, is obtained from a balance of interfacial tensions (Figure 1) and is defined from Young's equation, according to which
slv.cosq + sls = ssv
where slv, sls, and ssv are the interfacial tensions at the boundaries between liquid (l), solid (s), and vapor (v). Here, s represents the force needed to stretch an interface by a unit distance (or, equivalently, energy required to create a unit surface area of a given interface, provided that, in the case of ssv, mechanical distortion and strains are negligible). The condition q < 90° indicates that the solid is wet by the liquid, and q > 90° indicates nonwetting, with the limits q = 0 and q = 180° defining complete wetting and complete nonwetting, respectively. This article reviews the status of high-temperature wettability as manifested in the contact-angle phenomena, with a focus on the behavior of metallic coatings in contact with liquid metals.
A large body of useful scientific information about the wettability of and
spreading upon high-temperature metal and ceramic coatings comes from the application
of Young's equation to metallurgical systems at elevated temperatures. Young's
equation is also used as a foundation for interfacial studies in a variety of
other fields. Despite its success in offering practical insight into the wettability
and spreading phenomena, however, Young's equation has been the subject of considerable
controversy and debate.
Gravitational Effects
Young's equation predicts a unique value of the equilibrium angle, q,
in terms of thermodynamic quantities (s's) without
regard to the presence of external fields, such as gravitation. This is in contrast
to the common observations of shape distortion of droplets on an inclined plane
in the earth's gravity. Theories and experiments3-5
have been advanced both to challenge and support Young's equation.
Gravity also influences gas adsorption at nonwetting rough surfaces;6
it opposes adsorption because the gas has to locally lift the liquid to enter
into surface troughs. Gas adsorption effectively smoothens the surface because
the liquid contacts only a portion of the asperities. However, adsorption creates
additional solid-gas and liquid-gas interfaces, and will be energetically favored
in a gravitational field if the decrease in ssl
due to reduced roughness is greater than the energy increase due to the creation
of additional surface.6
Substrate Deformation
Young's equation applies only to one-dimensional spreading and becomes invalid
if the substrate is not rigid and the contact-line motion takes place in both
horizontal and vertical directions. The force equilibrium of Figure
1 ignores the vertical component of the surface tension, slv
sinq, which acts along the line of contact (this
force is not countered by the weight that acts at the center of mass). As the
capillary forces are not balanced, external forces must be applied to the solid
to achieve equilibrium;7-9
these forces can produce deformation in highly deformable solids, such as gels
and rubber, destroying the coplanarity of interfacial tensions assumed in Young's
equation and causing ridge formation at the interfacial region. A quasi-equilibrium
could, however, exist within the window of time when an observation is made,
provided the solid's deformation rate is small.
The extent of deformation has been calculated using linear, isotropic, continuum
elasticity theory for thin plates, membranes, and plates.9
Ridge formation at the wetting front also occurs in high-temperature systems
because of interfacial chemical reactions and diffusion processes.
Precursor Films and Microscopic Angles
In many solid-liquid systems, the liquid front is spearheaded by a thin foot
or a precursor film that forms when the liquid develops a finite, non-zero curvature
near its periphery due to local intermolecular interactions.1,10
A sharp distinction between solid, liquid, and vapor phases can no longer be
assumed as the liquid is gradually thinned, yielding a microscopic angle that
does not obey Young's equation.11
This is because the continuum concept of surface energies to represent the local
molecular interactions becomes increasingly tenuous for precursor films approaching
molecular thicknesses.
Vapor Adsorption
If the liquid vapor is adsorbed on the solid's surface, the surface tension
of the solid, ssv,
decreases. The concept of a spreading pressure P
(defined from P = ss
- ssv) is related
to the need to maintain a saturated vapor of the liquid around the solid.1,12
Here, ss is the
surface tension of the solid in equilibrium with its own vapor or in vacuum,
and ssv is the
surface tension of the solid in equilibrium with the saturated vapor of the
liquid. If the spreading pressure can be neglected (which is true for q
> 10°), then it is possible to write the Young equation in terms of the true
or intrinsic surface tension of the solid. Techniques have been devised to test
whether the spreading pressure in a given system is negligible and the measured
contact angle is indeed the equilibrium angle.1
Surface Roughness
Young's equation applies to ideal surfaces that are perfectly smooth and devoid
of all chemical and structural inhomogeneities. The contact angle measured on
a rough surface (called the Wenzel angle, qw)
does not obey Young's equation; it is related to the equilibrium (Young) angle
qy, from Reference
13
cosqw = rcosqy
where r is the ratio of the true wetted area to the apparent area.
Wenzel's equation applies to equilibrium angles on rough surfaces and not to
advancing and receding angles of a droplet on a rough solid surface that give
rise to contact-angle hysteresis. Hysteresis, H, is defined as the difference
of the advancing and receding angles (i.e., H = qa
- qr) and arises
because the liquid-vapor interface does not retrace its original path when it
recedes on the solid, so that spreading is thermodynamically irreversible.1,14-19
Because roughness hinders the contact line motion by creating energy barriers,
the system can reside in any of the potential wells accessible to it that are
commensurate with the vibrational (or thermal) energy of the droplet.1
The advancing angle is less sensitive to roughness than is the retreating angle
and is usually the one measured and reported.
As surface inhomogeneities exceeding about 10 nm in size can anchor the contact
line, contact-angle hysteresis is pervasive in most systems save the most carefully
prepared smooth and homogeneous surfaces. Applying acoustic energy (vibrations)
diminishes the contact-angle hysteresis. In the case of reactive systems, the
additional contact area due to roughness could enhance the chemical attack provided
that the high surface tension of the liquid does not restrict the asperity contact
with the liquid and gas entrapment at the rough interface does not minimize
the solid-liquid contact.
Most solid surfaces (with the exception, perhaps, of single crystals) are seldom
consistent and clean, with different surface domains possessing different chemistries
and wetting properties. Such chemical inhomogeneity could result from oxidation,
corrosion, coatings, multiple phases (e.g., eutectic), adsorbed films, ledges,
kinks, dislocations and grain-boundary intersections with the surface, and crystallographic
anisotropy (planes having different packing density and exposing different molecular
groups). Wettability and spreading are sensitive to such chemical and structural
inhomogeneity.1,17,20-28
Carefully prepared single crystals are closest to idealized surfaces, and several
studies have focused on the wetting behavior of single crystals by metallic
melts.29-33
The wettability on chemically inhomogeneous surfaces is conveniently characterized
in terms of an effective contact angle. The effective equilibrium contact angle
on a composite surface constituted by chemical phases having different area
coverages and contact angles is the area-fraction-weighted angle,20
provided there is no hysteresis. Like Wenzel's equation for roughness, the weighted-average
rule applies to the equilibrium state rather than to metastable states. Note
also that chemical reactions are often accompanied by reconstruction of the
solid's surface, which could promote the chemical inhomogeneity and roughness.
For example, in the SiO2-Al system, the reduction
of silica by aluminum leads to a 38% volume reduction, which causes cavities
to develop ahead of the contact line, thereby enhancing the roughness and hampering
the spreading.15
Wettability is manifested in numerous forms in a variety of coating processes.
In many industrial processes, the substrate is immersed in a liquid coating
material, then withdrawn to leave a liquid film on the substrate. The film (coating)
thickness depends upon the surface tension, withdrawal speed, substrate geometry,
roughness, and melt viscosity.34-36
The dispersion of fine, granular solids in a liquid vehicle is a basic step
in preparing paints and other coating materials and involves particle transfer
across a gas-liquid interface. The transfer of nonwettable solids into liquids
requires the solid to overcome a surface energy barrier at the liquid-gas interface,37-44
and energy must be expended to assist the transfer of nonwettable solids. Once
the solid enters the liquid, the capillary (attractive) forces and gas bridges
between solids control such phenomena as agglomeration, dispersion, and air
entrapment.45-51
The interparticle forces between dispersed solids are due to liquid surface
tension and pressure difference across the curved liquid-vapor boundary between
contacting solids. The maximum interparticle force, F, due to capillary forces
between two touching spheres is49
F = 2(2)1/2slv cosq/R
where R is the radius of the sphere. The force increases with increasing liquid
surface tension and decreasing contact angle and particle radius. These forces
affect the viscosity, density, and sedimentation behavior of the suspension
and the properties of the coating deposited using the suspension. Other coating
processes, such as thermal spray, which atomize and spray molten or semimolten
coating materials, also involve surface energetic considerations. These considerations
become important in the shredding of droplets during flight and upon impact
on the substrate, as well as in the engulfment of fine particulates into atomized
droplets during flight in the case of composite coatings.52,53
The angle of contact as given by Young's equation is a static (equilibrium)
angle. However, during its motion toward an equilibrium shape, a liquid droplet
scans a range of apparent (dynamic) contact angles. The dynamic angle depends
upon the rate of spreading,10,54-65
and several contact angle-velocity relationships have been proposed in the literature
(Table I). In reactive systems,66-82
however, the wetting dynamics are interactively coupled with the reaction kinetics,
and the spreading behavior becomes complex and less clear. Whereas equilibrium
wetting is achieved rapidly (at times on the order of 10-4-0.1
seconds) in inert systems, equilibrium could take from 100 seconds to more than
10,000 seconds in reactive systems.
|
Table I. Models for Spreading Kinetics
of Liquids on Solids
|
|||
| Model/Reference
|
Assumptions
|
Kinetic Law
|
Comments
|
| DeGennes10 | Semi-empirical model for inert liquids, applied U ~ q relationship for forced flow of liquids through tubes to droplet spreading | a10 ~ t | Widely used for polymeric liquids on low energy solids |
| Van Remoortere and Joos54,64 | Empirical model | a7 ~ t | Applies to inert liquids such as silicone oil and parafin oil on silane- and parafin-coated glass |
| Yin63 | Determines the velocity distribution in the spreading droplet, considers viscous drag as the resisting force, spreading scales with (slv/m) | a5 ~ t | Applies to molten polymers on smooth surfaces (Al, mica, teflon) |
| Fritz65 | Determines velocity-dependence of dynamic angle from hydrodynamic analysis of flow in a capillary prewetted with a thin film of finite thickness, bulk viscosity is the major resting force | a10 ~ t | |
| Dodge-Blake-Haynes55,59 | Applies absolute reaction rate theory to spreading, wetting front assumed to propagate over periodic potential wells between adsorption sites | a7 ~ t | Combines surface physics and fluid mechanics approaches, predicts indefinite spreading |
| Eustathopoulos66,67 | Semi-empirical model, consistent with linear spreading in several high-temperature couples | a ~ t | Models reactive spreading with interface-control, consistent with Al/vitreous C, CuAgTi/alumina, and other systems |
| Mortensen et al.70 | Diffusion field at the wetting front limits advance, models reactive spreading kinetics under steady-state diffusion | a4 ~ t | Models reactive spreading with diffusion-control, limited experimental verification,69 ignores convection |
| Ambrose et al68 | Identifies flow regimes consistent with models for inert liquids, applies empirical equations to model flow regimes inconsistent with such models | a ~ exp (t/3t) | Presentational approach, does not identify flow mechanisms, applies to reactive brazes82 and some ceramic-metal couples81 |
|
|
|||
There is evidence that models for the spreading of inert liquids provide a useful
framework to understand the flow behavior in reactive systems.68,81
For example, the spreading kinetics during the initial and final stages of Ni-P
braze over Fe-Cr substrates are consistent with the deGennes equation.68
In the intermediate flow regime, an (empirical) exponential relationship appears
to be valid. Spreading kinetics consistent with an exponential behavior is also
observed in PbSn-Cu, Hg-Ag, AuSi-SiC, CuTi-Al2O3,
and several other systems.81
As a first step toward understanding the complex spreading behavior of reactive
systems, a presentational approach can be used to identify different flow regimes
that are consistent with the classical models for simple liquids. An example
of such an approach is shown in Figure
2, where the spreading data in several reactive couples are plotted as ln
a versus ln t, where a is the instantaneous radius of the spreading droplet,
and t is the time. If the classical models (developed chiefly for viscous polymers
and similar inert liquids) were applicable to reactive spreading, then the ln
a vs. ln t data in each system would fit a straight line consistent with such
relationships as a5 ~ t (Yin63),
a7 ~ t (Remoortere and Joos54,64
and Dodge59), or a10
~ t (deGennes10 and Friz65).
Each system of Figure 2,
however, displays a complex spreading behavior, exhibiting several different
flow patterns. Some of these patterns appear to be broadly consistent with the
behavior predicted by the classical models (Table II);
whereas, others seem to follow either a linear (a ~ t) or a power law (a4
~ t) behavior characteristic of reaction- and diffusion-controlled spreading
mechanisms,66,69,70
respectively. Still other flow regimes appear to be inconsistent with all previous
models.
|
Table II. Model Approximations to
Spreading in Reactive Couples (Figure
2)
|
||||
| System
|
Temperature (K)
|
Kinetics
|
Model
|
Slopes of Linear Segments in Figure 2 (mm/s) |
| Cu-9.5Ti/sapphire |
1,35083
|
a10
~ t
|
0.10 (Fig. 2d)
|
|
| Cu-9.5Ti/sapphire |
1,35083
|
a2.4
~ t
|
-
|
0.42 (Fig. 2d)
|
| Cu-9.5Ti/sapphire |
1,35083
|
a50
~ t
|
-
|
0.02 (Fig. 2d)
|
| Cu-9.5Ti/sapphire |
1,35083
|
a4
~ t
|
Mortensen et al.70
|
0.25 (Fig. 2d)
|
| Cu-12.6Ti/sapphire |
1,35083
|
a50
~ t
|
-
|
0.02 (Fig. 2d)
|
| Cu-12.6Ti/Al2O3 |
1,35083
|
a10
~ t
|
0.10 (Fig. 2d)
|
|
| Ag-38Cu-3.7Ti/Al2O3 |
1,22382
|
a10
~ t
|
0.11 (Fig. 2a)
|
|
| Pb-40Sn/Cu |
52384
|
a25
~ t
|
-
|
0.04 (Fig. 2c)
|
| Pb-40Sn/Cu |
52384
|
a6.9
~ t
|
0.15 (Fig. 2c)
|
|
| Pb-40Sn/Cu |
52384
|
a1.6
~ t
|
-
|
0.63 (Fig. 2c)
|
| Pb-30Sn/Cu |
53384
|
a25
~ t
|
-
|
0.04 (Fig. 2c)
|
| Pb-30Sn/Cu |
53384
|
a5
~ t
|
Yin63
|
0.21 (Fig. 2c)
|
| Pb-50Sn/Cu |
49384
|
a10
~ t
|
0.10 (Fig. 2c)
|
|
| Pb-50Sn/Cu |
49384
|
a25
~ t
|
-
|
0.04 (Fig. 2c)
|
| Pb-50Sn/Cu |
49384
|
a4
~ t
|
Mortensen et al.70
|
0.24 (Fig. 2c)
|
| Pb-50Sn/Cu |
49384
|
a50
~ t
|
-
|
0.02 (Fig. 2c)
|
| Cu-12.6Ti/sapphire |
1,35084
|
a6.9
~ t
|
0.14 (Fig. 2d)
|
|
| Cu-12.6Ti/sapphire |
1,35084
|
a6
~ t
|
-
|
0.17 (Fig. 2d)
|
| Ni-11P/Fe20Cr |
1,20368
|
a10
~ t
|
0.11 (Fig. 2a)
|
|
| Ni-11P/Fe20Cr |
1,20368
|
a4.3
~ t
|
Mortensen et al.70
|
0.23 (Fig. 2a)
|
| Ni-11P/Fe20Cr |
1,20368
|
a10
~ t
|
0.11 (Fig. 2a)
|
|
| Au-Si/SiC |
-85
|
a10
~ t
|
0.10 (Fig. 2b)
|
|
| Au-Si/SiC |
-85
|
a1.2
~ t
|
Eustathopoulos66
|
0.83 (Fig. 2b)
|
| Au-Si/SiC |
-85
|
a3.3
~ t
|
-
|
0.30 (Fig. 2b)
|
|
|
||||
Note, however, that the spreading kinetics in a given system is strongly affected
by the experimental conditions, and very different spreading kinetics can be
measured for the same system depending upon the experimental technique (oxygen
partial pressure, temperature, alloying technique, surface preparation, etc.).
Thus, while the presentational scheme of Figure
2 illustrates the complexity of the reactive spreading phenomenon vis-à-vis
inert liquids, it does not shed light upon the underlying mechanisms. On the
other hand, characterizing the detailed mechanisms that govern the coupling
of chemical reactions and wetting dynamics of spreading droplets in reactive
systems affords considerable insight into chemical-reaction-enhanced wettability.
The complex nature of reactive spreading in high-temperature systems is also
revealed in the plots of spreading data in the form cosq/cosq0
versus the parameter slv
t/m in Figure
3, where q and q0
are the instantaneous and equilibrium values of the contact angle, q;
t is time; and slv
and m are the surface tension and the viscosity of
the liquid, respectively. While the contact-angle data of Figure
3 display trends relative to the ratio slv/m
(corrected for the test temperatures using the data from References
96-98), there is a large dispersion in the wettability data. In contrast,
the cosq/cosq0
versus slvt/m
data for inert liquids can be made to collapse into a master curve57
(after normalizing svt/m
by an arbitrary length scale).
Several recent studies66,72,79,99-170
have presented the high-temperature wettability data in numerous systems and
attempted to model the complex interfacial phenomena that occur during reactive
spreading, offering insights into the coupling of interfacial reactions and
spreading kinetics. Several configurations have been conceptualized for the
reactive-spreading phenomenon, such as viscous spreading at t ≈ 0, reminiscent
of classical liquids (but perhaps outside the observational domain for reactive
liquids); ridge formation due to chemical reactions and pinning of the wetting
front; evaporation-condensation and/or adsorption of reactive species; nucleation,
growth, and coalescence of reaction products at the solid-liquid interface (and
lowering of ssl);
and, finally, spreading on a reacted layer ahead of the fluid meniscus.
Kinetics
In complex reactive systems, chemical reactions, solute segregation, wetting,
and spreading are interactively coupled. Conceptually, spreading can be divided
into distinct stages. The first stage is the very rapid spreading under the
driving force for the balance of interfacial tensions characteristic of inert
liquids. In the second stage, the substrate dissolves in the liquid and forms
compounds, initially as discrete crystals that nucleate on preferred sites at
the solid-liquid interface, and later grow to form a continuous layer of the
reaction product(s). Such reactions yield one or more interfaces in place of
a single solid-liquid interface. Subsequently, a reaction band forms around
the droplet that grows by the processes of surface, bulk, and short-circuit
diffusion paths.
Two limiting behaviors of reactive spreading are identified: systems exhibiting
relatively rapid reaction rates (e.g., Al2O3/CuTi),
where solute diffusion is rate-limiting and the spreading velocity decreases
with time, and systems exhibiting relatively sluggish reaction kinetics (e.g.,
C/Al), where long-range mass transport (diffusion) is rapid relative to the
rate of local chemical reactions, and spreading velocity is roughly constant.
Diffusion-Controlled Spreading
In the diffusion-controlled spreading of liquid droplets,66,69,70,77,168,
171-174 the meniscus advance is limited by
the rate of arrival at the reaction front of the reacting species via diffusion.
The diffusion field at the reaction front continuously decreases in time as
the droplet spreads to a thin hemispherical cap.
The effect of diffusion on spreading has been modeled69,70
by assuming that the curvature effects and convection are negligible, and the
spreading droplet is a semi-infinite medium with the thin layer of reaction
product at the interface essentially serving as a diffusion barrier. The model
shows that the fourth power of droplet radius, a, varies linearly with the product
of droplet volume, V, and spreading time, t, according to Reference
70
a4 = KVt
This is in contrast to the linear relationship between R and t that is obtained
when the reaction kinetics control the spreading process.
Reaction-Controlled Spreading
In couples such as Al/vitreous C, CuAgTi/Al2O3,
and some other systems, linear spreading kinetics is observed, and the droplet-base
radius increases linearly with time.66,67,165
In such systems, chemical reactions modify the solid's surface and control the
spreading. The initial contact angle is usually large because of the surface
oxides that resist spreading. As the deoxidization at high temperatures and
under high vacuum erodes the surface oxides, the dynamic angle, q,
drops, and high spreading rates, characteristic of inert liquids on untransformed
solid, are achieved. However, once solid reaction products form at the interface,
the spreading rate adjusts consistent with the wettability of the product phase.
For example, in the Al/vitreous C system, the growth of the (nonwetting) product
phase, Al4C3,
slows down the spreading. The droplet base radius increases linearly with time,
and a constant spreading rate is attained for several hours (e.g., 3.2 h for
Al/vitreous C67). Upon
prolonged holding, the product layer extends beyond the droplet periphery, and
eventually a stable contact angle is attained. As the reaction layer growth
overtakes the wetting front, atomic diffusion through the product layer limits
further growth. The driving force for spreading is
slv [cosqeq - cosq(t)]
where qeq and q(t) are the equilibrium and instantaneous values of the contact angle of the liquid on reacted layer, respectively. As q(t) tends toward qeq, the driving force for spreading decreases, and eventually flow ceases when qeq is attained.
High-temperature wettability is influenced by a large number of variables that
include temperature; contact time; atmosphere; roughness; crystal structure;
composition; surface pretreatments; and interfacial segregation, adsorption,
and reactions. Extensive reviews have been published documenting the role of
factors that govern wettability.25,66,72,99,116,169,175-177
Basically, three types of interactions can promote wettability in the high-temperature
solid-liquid systems: dissociation of surface oxides on liquid metal (oxide
scavenging), chemical dissolution of the solid in the melt and interfacial adsorption
of reactive solutes (reduction of ssl),
and formation of a wettable interfacial compound.
At high temperatures, spreading to an equilibrium shape becomes difficult when
a solid reaction product (e.g., an oxide) on the liquid opposes the spreading,
resulting in a large value of the contact angle. The stability and protective
influence of oxide films is affected by the temperature, atmosphere, and alloying
elements. An ultrahigh vacuum erodes the film to form gaseous suboxides at high
temperatures, thereby establishing a physical contact and yielding a sudden
drop in the contact angle above a critical temperature. Other chemical species
present in the atmosphere could affect the wettability. Thus, reaction of water
vapor in the test chamber with the graphite susceptor used for induction heating
or with the test substrate could form CO and H2.
Carbide substrates, such as SiC, could graphitize and form free carbon following
silicon sublimation at high temperatures. High temperatures decrease the liquid-surface
tension (dslv/dT
< 0) and promote wettability. Also, the spreading rate toward equilibrium is
enhanced because of diminishing liquid viscosity at high temperatures.
The liquid composition markedly influences its wettability with solids. Thus,
chromium and titanium in copper make the Cu/graphite system a wettable one.
Likewise, silicon in Al/SiC, magnesium in Al/silica and Al/alumina, and titanium
in Al/C all improve wetting although the mechanisms of wetting enhancement are
different. Thus, a high silicon content in Al/SiC reduces the propensity for
nonwetting Al4C3
formation; whereas, titanium in Al/C promotes wetting by TiC formation. Similarly,
magnesium in Al/SiO2 and Al/Al2O3
scavenges the surface oxides and forms wettable reaction products (e.g., spinel
MgAl2O4).
The dissolution of oxygen in some metals improves wetting and bonding as observed
in Cu/AlN, Cu/SiC, and alumina/Cu.
The wettability-enhancing interfacial reactions are limited by interface kinetics,
diffusion rate, or a combination thereof. Once a thin product layer forms, growth
is usually limited by diffusion through this layer, and the thickness increases
parabolically with time,
X = k√t
where k is a parabolic reaction-rate constant, and t is time. Modifications
of the simple parabolic law are necessary to account for nonplanar interfaces;
diffusion in a finite domain (soft impingement); formation of intermediate nonequilibrium
phases; and the existence of short-circuit diffusion paths, such as interfaces,
grain boundaries, and dislocations.
The nature of atomic bonding and the thermodynamic stability of solids in contact
with liquids are related to their wettability at high temperatures. In the case
of carbides, wettability decreases with increasing heat of formation of the
carbide. The high heat of formation implies strong interatomic bonds and correspondingly
weak interaction with metals. In the case of oxides, wettability decreases with
an increase in the free energy of oxide formation. Highly ionic ceramics, such
as alumina, are relatively difficult to wet since their electrons are tightly
bound. On the other hand, covalently bonded ceramics are more easily wetted
by metals than highly ionic ceramics because of a similarity between metallic
and covalent bonds. Fundamental atomic bonding and thermodynamic stability considerations
have led to the development of several predictive models of wetting (Table
III).
|
Table III. Models for Predicting Wetting
Behavior
|
|||
| Model/Reference
|
Main Assumptions
|
Predictive Relationship
|
Comments
|
| McDonald-Eberhart178 | Wettability of oxides by metals related to oxygen affinity, work of adhesion, Wad, related to free energy of oxide formation | 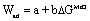 a, b are constants, a related to physical dispersion forces, DGMeO = free energy for oxide formation |
Interfacial segregation not considered, predictions of Wad inconsistent with observations in some systems |
| Naidich72 | Relates wettability to DG for S-L reaction near the interface composed of two monolayers (one on liquid side and the other on solid side) | Applies to Sn/NiO, Ti/MgO, Zr/MgO and other couples | |
| Laurent-Drevet-Eustathopoulos118 | Relates wettability to intensity of reaction and wettability of the resulting interface, identifies wettability of resulting interface as a key factor | q0 = contact angle in the absence of reaction, Dsr = change in the interfacial energy due to reaction, DG = Gibb's free energy change for the reaction |
|
| Zisman175 | Applies to low-energy solids, identifies critical surface tension for complete wetting | sc = critical surface tension 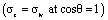 |
|
| Neumann179-182 | Semi-empirical equation-of-state to predict the surface energies | 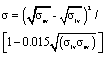 |
Validated in low-temperature systems, applied to ceramic-metal systems,183-185 disagrees with some grain-boundary grooving data,186 criticized on theoretical grounds187,188 |
| Good-Girifalco1,189 | Relates surface energies via an interaction parameter (F), adhesion energy obtained from a geometric combining rule for solid-solid and liquid-liquid pairs, F calculated from polarizabilities, dipole moments, ionization potentials | F = 0.5 to 1.0 |
Applies to low-temperature systems |
| Wu190 | Uses Zisman's critical surface tension, calculates sc of any solid using q of any one test liquid | Applies to polymers and organic solids | |
| Rhee191,192 | Utilizes Zisman's critical surface tension sc for high-energy solid-liquid systems at high temperatures | b = constant |
Applies to MgO, BeO, UO2, and other solids |
| Warren193 | Applies solution thermodynamics to estimate the s-l surface energy, considers chemical and structural contributions to surface energies | s's given in terms of bulk and interface compositions, latent heat, melting point, and molar volumes |
|
| Miedema194,195 | Solution thermodynamics approach, considers surface segregation effects | Applies to liquid metals and intermetallic compounds | |
|
|
|||
From a practical standpoint, the coating-substrate adhesion is also of essence.
Physical, chemical, and mechanical interactions influence adhesion. For purely
mechanical adhesion to develop, the liquid coating material must be able to
penetrate the surface porosity in the solid, a phenomenon governed by the interaction
of capillary forces driving the penetration (in a wettable system) and the retarding
forces due to viscosity and gravity (depending upon the penetration geometry).196-199
In reactive systems, however, additional complexities arise during liquid penetration
because of the transient nature of reaction-driven wettability and pore-size
reduction and closure due to reaction-product deposition within pores.101,200-203
Such considerations are also important in joining technologies and reactive
infiltration of composites.
A large body of data on high-temperature wettability and interfacial bonding
is available for materials such as SiC,32,85,113,123-125,138,153,157,170,204-211
Al2O3,72,126-128,130,162,212-220
mullite,221-223 carbon,117,145,146,155,
165,170,224-236
fluoride (CaF2, BaF2,
MgF2),33
silica,158,221,237,238
nitrides (AlN, TiN, BN, Si3N4),72,154,159,239-242
CaO,243 TiO2
and ZrO2,134,136,137,147
boron,72 MgO,72
metals (silver, copper in contact with tin, bismuth, SnBi, SnPb),28,31,75,76
and other materials.
The influence of material and test parameters on the high-temperature wettability
has been extensively investigated, particularly the effects of alloying;33,111,113,128,134,136-140,155,206-209,231-236,244,245
atmosphere;72,85,141,147,207,246
temperature;90,91,124,125,151,205
time;123-125,151,153,155
ceramic structure/composition (single- vs. polycrystal, crystal orientation,
hot pressed, reaction bonded, surface porosity, etc.);29,30-33,72,130,155,166,216,218,234
and surface modification using metallic coatings,160,211,227,228
oxide coatings,247-250
carbon coatings,148
and fluoride coatings.225,230
The effects of some of these factors are discussed in greater detail in Reference
169.
Figures 4 through 13 show the high-temperature wettability data and interface
microstructure for liquid metals, primarily aluminum and copper, on a variety
of coated- and monolithic substrates.90,144,169,234,251-257
In the case of aluminum alloys, there is no remarkable difference in the wetting
behavior on monolithic substrates and a thin layer of the same material. Small
differences noted at the beginning of the wetting process are probably caused
by the heterogeneity in the structure and chemistry of multicomponent bulk materials
(in contrast, coatings were more homogeneous).
In the Al/alumina system (Figure
4), the lowest contact angles are obtained with the coatings of NiP and
NiCoP.169,252
Figure 5a shows the
effect of alloying and coating type on the wettability kinetics in the Al/alumina
system; Al-Si alloys form contact angles almost twice as large as pure aluminum
due to the inhibition of the dissolution of the silicon-containing coating material
(Cr-42Si-9W) in the alloy, which also contains silicon.252
In the case of Al-Ti alloys on alumina, a comparison of Figures
4c and 5b indicates
that in spite of the semi-solid state of the Al-10Ti alloy at the test temperature,
it exhibits a wetting behavior similar to molten pure aluminum, characterized
by good wetting of Ni-, CoP-, and NiCoP-coated alumina substrates. The same
coatings applied to graphite improve its wettability with aluminum (Figure
6), resulting from the dissolution of the coating in the liquid droplet
(Figures 7 and 8).
However, in spite of good wetting, the strength of the droplet/coating/substrate
joint may be weak if the bonding between the substrate and the coating is poor.
Figure 8 illustrates
such a situation for the Al/Cu/graphite system; the aluminum drop is detached,
along with copper coating from the graphite substrate, because of a lack of
chemical interaction between copper and carbon.
Complete dissolution of a coating might lead to dewetting; therefore, the time,
temperature, atmosphere, and other process parameters must be judiciously selected.
It is interesting to note that in the case of metallic coatings made by chemical
reduction from salt solutions, the effect of wettability improvement is very
stable, even when complete dissolution of the coating, confirmed by optical
microscopy, takes place (Figure
7c). Studies169,256
on the effect of aluminum alloying additions on wettability improvement in the
Al/graphite system clearly indicate that nickel and copper additions do not
ensure good wetting (Figure
9), and in copper- or nickel-rich aluminum droplets, the dissolution of
the coating is not responsible for the stable effects of wettability enhancement.
Unlike the situation in a sessile-drop test, however, nickel- and copper-coatings
on ceramic reinforcements reduce the threshold pressure for infiltration and
yield larger penetration lengths, indicating improvements in the wettability.210,211
In such pressurized infiltrations tests, however, the contact times are on the
order of a few tens of seconds, and spreading is completed prior to the attainment
of equilibrium wettability.
Another interesting aspect of the wetting behavior of coatings is the effect
of the substrate on equilibrium wetting in a sessile-drop test. The coatings
of a similar chemical composition deposited using similar procedures show different
wetting properties with a given metal depending upon the type of substrate material
on which the coating is applied. For example, metallized graphite substrates
show lower contact angles with aluminum compared to alumina substrates (Figure
10).
Contrary to technological coatings developed to promote wettability, certain
types of barrier coatings are employed to protect the substrate materials from
the aggressive attack of different environments. For example, in metallurgical
and foundry practices, barrier coatings are used to increase the lifetime of
crucibles, dies, and other appliances that routinely come in contact with molten
metals. In such cases, the engineered coatings must impair the wettability and
minimize the spreading and contact area. Figure
11 illustrates the effect of boron nitride (lubricant) coating (BNlub;
dry composition is 87% BN and 13% Al2O3)
on the wetting behavior of an aluminum droplet containing 10 wt.% titanium on
a graphite substrate. Although the Al-10Ti alloy droplet is semi-solid at the
test temperature, a strong chemical interaction between titanium and carbon
yields significant wettability improvements, that, depending upon graphite type,
results either in infiltration or erosion of the substrate material.234
The application of a BNlub coating provides
effective protection against such attack in the case of aluminum alloys, but
the same coating might play a negative role in contact with other materials
containing active alloying elements. For example, as shown in Figure
12, Cu-Ti alloys wet graphite at high titanium contents (~ 17 wt.%), but
BNlub coatings on graphite provoke a sudden
decrease in the contact angle of Cu-10.5Ti alloy (Figure
12a), consistent with the data for Cu-Ti/BN system (Figure
12b). Additionally, the BNlub coating
cracks due to stresses generated during the formation of titanium-rich reaction
products, such as TiN and TiB2 (Figure
13). Finally, because of a very strong interfacial bond at the BNlub/graphite
joint, a dramatic situation is encountered wherein the graphite substrate completely
cracks through its thickness of about 5 mm (Figure
13). Such a situation is inadmissible in practice because it may cause breaking
of crucibles, dies, and other appliances in contact with reactive melts.
The performance of a coating during service depends not only on the inherent
characteristics of the coating (and substrate) materials but also on the coating-substrate
adhesion. Wettability promotes adhesion through physical, chemical, and/or mechanical
bonds acting across the coating-substrate interface. As the interface represents
a region of compositional and structural discontinuities, it is inherently unstable
and evolves during service, serving as a site for morphological, chemical, and
structural transformations. Additionally, the interface topography is important
because it affects the stress concentration and crack-deflection paths.
Adhesion develops from physical (e.g., weak van der Waals) bonds, chemical interactions,
and friction from irregular surface topography. Residual stresses arising from
the mismatch of coefficients of thermal expansion (CTE) between the coating
and substrate during temperature excursions influence the adhesion; CTE mismatch
gives rise to stresses that could cause interfacial cracking and debonding if
these stresses are not accommodated by plastic flow. Stress-absorbing compliant
layers are used to promote the thermoelastic compatibility between dissimilar
materials. Similarly, reaction-barrier coatings are used to protect the underlying
solid from chemical degradation; however, all such layers introduce additional
interfaces that must meet appropriate criteria for material compatibility.
The effect of wettability on interface adhesion can be quantified by the work
of adhesion, WAd, which is defined as1
Wad = slv (1 + cosq)
A high work of adhesion indicates good wetting; whereas, a low work of adhesion
indicates poor wetting. The work of adhesion, Wad,
between metals and oxide ceramics (primarily alumina) correlates with both the
tensile strength and bend strength of the metals,258,259
suggesting that good wetting generally yields good interface bonding. This has
been confirmed (Figure
14) experimentally using shear tests directly on (solidified) sessile drop
test specimens.255
The inherent plasticity of the material is also important; metals with a low
yield strength could cause plastic flow and provide for blunting of the interfacial
cracks, resulting in higher interfacial toughness and low stress concentration
even when the interface chemistry is not such as to ensure good wetting. In
other words, good wetting resulting from chemical reactions may not be a necessary
precondition for achieving a high adhesion strength.258
More complete discussions of the relationship between wettability, adhesion,
and interface processes have been presented in References 72,
132, 154, 169,
258-273.
References
1. A.W. Neumann and R.J. Good, Surface and Colloid Science,
vol. II, ed. R.J. Good and R.R. Stromberg (New York: Plenum
Press, 1979).
2. L.E. Murr, Interfacial Phenomena in Metals and Alloys
(New York: Addison Wesley
Publ. Company, 1974).
3. B.A. Pethica, J.
Colloid Interface Sci., 62 (3) (1977), p. 567.
4. J.P. Garandet, B. Drevet, and N. Eustathopoulos, Scripta
Mater., 38 (9) (1998), p. 1391.
5. Y. Liu and R.M. German, Acta
Mater., 44 (4) (1996), p. 1657.
6. H. Sakai and T. Fujii, J.
Colloid Interface Sci., 210 (1999), p. 152.
7. G.R. Wickham and S.D.R. Wilson, J.
Colloid Interface Sci., 51 (1) (1975), p. 189.
8. G.R. Lester, J.
Colloid Sci., 16 (1961), p. 315.
9. M.A. Fortes, J.
Colloid Interface Sci., 100 (1) (1984), p. 17.
10. P.G. de Gennes, Rev. Modern Phys., Part I, 57
(3) (July 1985), p. 827.
11. G.J. Jameson and M.G. Delcerro, J. Chem. Soc. Faraday
Trans., 72 (1) (1976), p. 883.
12. M. Morra, E. Occhielo, and F. Garbassi, Prog. in
Surf. Sci., p. 79.
13. R.N. Wenzel, Ind. Eng. Chem., 28 (1936), p. 988.
14. X.B. Zhou and J.Th.M. De Hosson, J.
Mater. Res., 10 (8) (1995), p. 1984.
15. X.B. Zhou and J.Th.M. De Hosson, Acta
Mater., 44 (2) (1996), p. 421.
16. V. de Jonghe and D. Chatain, Acta
Metall. Mater., 43 (4) (1995), p. 1505.
17. J. Drelich and J.D. Miller, J.
Colloid Interface Sci., 164 (1994), p. 252
18. H. Nakae et al., Acta
Mater., 46 (7) (1998), p. 2313.
19. F.G. Yost, J.R. Michael, and E.T. Eisenmann, Acta
Metall. Mater., 43 (1) (1995), p. 299.
20. A.B.D. Cassie, Disc.
Faraday Society, 3 (1) (1948), p. 11.
21. A.W. Neumann et al., J.
Colloid Interface Sci., 71 (2) (1979), p. 293.
22. R. Asthana, Metall.
Trans., 24A (1993), p. 1673.
23. R. Asthana, Scripta
Metall. Mater., 29 (1993), p. 1261.
24. J.G. Li and H. Hausner, Scripta
Metall. Mater., 32 (3) (1995), p. 377.
25. A.W. Neumann and R.J. Good, J.
Colloid Interface Sci., 38 (1972), p. 341.
26. X.B. Zhou and J.Th.M. Hosson, Acta
Mater., 44 (2) (1996), p. 421.
27. R.P. Voitovich, Yu.V. Naidich, and G.A. Kolesnichenko,
Poroshk. Metall., English translation, 6 (354) (1992), p. 40 (New York:
Plenum Publ. Co., 1992, p.
494).
28. H.K. Kim, H.K. Liou, and K.N. Tu, J.
Mater. Res., 10 (3) (1995), p. 497.
29. N. Grigorenko et al., Proc. Int. Conf. High-Temperature
Capillarity - 97 (HTC-97), ed. N. Eustathopoulos and N. Sobczak (Krakow,
Poland: Foundry Research Institute, 1998), p. 133.
30. C. Rado, C. Senillou, and N. Eustathopoulos, in Ref.
29, p. 53.
31. F.G. Yost and E.J. O'Toole, Acta
Mater., 46 (14) (1998), p. 5143.
32. Y.V. Naidich, V. Zhuravlev, and N. Krasovskaya, in Ref.
29, p. 118.
33. Y.V. Naidich and V.P. Krasovsky, in Ref.
29, p. 87.
34. B.V. Derjagun and S.N. Levi, Film Coating Theory
(London: Focal Press, 1964).
35. D.A. White and J.A. Talimadge, AIChE
J., 13 (1967), p. 747.
36. A.R. Swenson and S.K. Nicol, J.
Colloid Interface Sci., 60 (3) (1977), p.568.
37. S. Hartland and J.D. Robinson, J.
Colloid Interface Sci., 35 (3) (1971), p.372.
38. A.V. Rapacchietta, A.W. Neumann, and S.N. Omenyi, J.
Colloid Interface Sci., 59 (3) (1977), p. 541.
39. A.V. Rapacchietta and A.W. Neumann, J.
Colloid Interface Sci., 59 (3) (1977), p. 555.
40. P.K. Rohatgi and R. Asthana, Cast Reinforced Metal
Composites, ed. S.G. Fishman and A.K. Dhingra (Materials Park, OH: ASM,
1988), p. 61.
41. P.K. Rohatgi et al., Metall.
Trans., 21A (1990), p. 2073.
42. J.M. DiMeglio and E. Raphael, J.
Colloid Interface Sci., 136 (2) (1990), p. 581.
43. H.M. Princen, J.
Colloid Sci., 18 (1963), p. 178.
44. O.J. Ilegbusi and J. Szekely, J.
Colloid Interface Sci., 125 (2) (1988), p. 567.
45. V.S. Yushchenko, V.V. Yaminsky, and E.D. Shchukin, J.
Colloid Interface Sci., 96 (2) (1983), p. 307.
46. V.V. Yaminsky et al., J.
Colloid Interface Sci., 96 (2) (1983), p. 301.
47. Ya.I. Rabinovich, Kolloidn. Zh., 39 (1977), p.
1094.
48. G. Ramani, T.R. Ramamohan, and B.C. Pai, Scripta
Metall., 24 (1990), p. 1419.
49. R.B. Heady and J.W. Cahn, Metall.
Trans., 1 (1970), p. 185.
50. J.W. Cahn and R.B. Heady, J.
Amer. Ceram. Soc., 53 (7) (1970), p. 406.
51. W.C. Carter, Acta
Metall., 36 (8) (1988), p. 2283.
52. L. Pawlowski, The Science and Engineering of Thermal
Spray Coatings (New York: John
Wiley and Sons, 1995).
53. E.J. Lavernia, J.A. Ayers, and T.S. Srivatsan, Int.
Mater. Revs., 37 (1992), p. 1.
54. P. Joos, P. van Remoortere, and M. Bracke, J.
Colloid Interface Sci., 136 (1) (1990), p. 189.
55. T.D. Blake and J.M. Haynes, J.
Colloid Interface Sci., 30 (3) (1969), p. 421.
56. W. Rose and R.W. Heins, J.
Colloid Sci., 17 (1962), p. 39.
57. H. Schonhorn, H.L. Frisch, and T.K. Kwei, J.
Appl. Phys., 37 (1966), p. 4967.
58. M.C. Phillips and A.C. Riddiford, J.
Colloid Interface Sci., 41 (1) (1972), p. 77.
59. F.T. Dodge, J.
Colloid Interface Sci. (1988), p. 154.
60. V.E.B. Dussan, J.
Fluid Mech., 77 (1976), p. 665.
61. I. Rivollet, D. Chatain, and N. Eustathopoulos,
J. Mater. Sci., 25 (1990), p. 3179.
62. S.J. Hitchcock, N.T. Carrol, and M.G. Nicholas, J.
Mater. Sci., 16 (1981), p. 714.
63. T.P. Yin, J. Phys. Chem., 73 (1969), p. 2413.
64. P. Van Remoortere and P. Joos, J.
Colloid Interface Sci., 160 (1993), p. 387.
65. G. Friz, Z. Angew. Phys., 19 (4) (1965), p. 374.
66. N. Eustathopoulos, Acta
Mater., 46 (7) (1998), p. 2319.
67. K. Landry and N. Eustathopoulos, Acta
Mater., 44 (10) (1996), p. 3923.
68. J.C. Ambrose, M.G. Nicholas, and A.M. Stoneham, Acta
Metall. Mater., 40 (10) (1992), p. 2483.
69. R. Voitovich et al., Acta
Mater., 47 (4) (1999), p. 1117.
70. Mortensen, B. Drevet, and N. Eustathopoulos, Scripta
Mater., 36 (1997), p. 645.
71. J.G. Li and H. Hausner, J. Mater. Sci. Lett.,
10 (1991), p. 1275.
72. Y. Ju. Naidich, Progress in Surface and Membrane
Science, ed. D.A. Cadenhead and J.F. Danielli (New York: Academic
Press, 1981).
73. P.R. Sharps, A.P. Tomsia, and J.A. Pask, Acta
Metall., 29 (1981), p. 855
74. F.G. Yost, Scripta
Mater., 38 (8) (1998), p. 1225.
75. X. H. Wang and H. Conrad, Metall.
Mater. Trans., 26A (1995), p. 459.
76. X. H. Wang and H. Conrad, Scripta
Metall. Mater., 31 (4) (1994), p. 375.
77. W.J. Boettinger, C.A. Handwerker, and U.R. Kattner,
The Mechanics of Solder Alloy Wetting and Spreading, ed. F.G. Yost et
al. (New York: Van Nostrand Reinhold,
1997), p. 103.
78. H. Nakae and A. Goto, in Ref. 29,
p. 12.
79. A. Meier, D.A. Javernic, and G.R. Edwards, JOM,
51 (2) (1999), p. 44.
80. R. Asthana, Metall.
Mater. Trans., 26A (1995), p. 1307.
81. R. Asthana, Scripta
Mater., 38 (8) (1998), p 1203.
82. M.G. Nicholas and S.D. Peteves, Scripta
Metall. Mater., 31 (1994), p. 1091.
83. J.G. Li, J. Mater. Sci. Lett., 11 (1992), p.
1551.
84. G.L.J. Bailey and H.C. Watkins, J. Inst. Metals,
80 (1951-52), p. 57.
85. B. Drevet, S. Kalogeropoulos, and N. Eustathopoulos,
Acta
Metall. Mater., 41 (1993), p. 3119.
86. J.J. Brennan and J.A. Pask, J.
Amer. Ceram. Soc., 51 (10) (1972), p. 569.
87. H. Fuji, H. Nakae, and K. Okada, Acta
Metall. Mater., 41 (10) (1993), p. 2963.
88. F.P. Chiaramonte and B.N. Rosenthal, J.
Amer. Ceram. Soc., 74 (3) (1991), p. 658.
89. T.J. Whelan and A.T. Anderson, J.
Amer. Ceram. Soc., 58 (9) (1975), p. 396.
90. N. Sobczak, J. Sobczak, and W. Radziwill, Proc. Int.
Conf. Composite Engineering (ICCE-3), ed. D. Hui, p. 777.
91. N. Sobczak et al., Proc. II Conf. Surf. Phenomena
in Foundry Processes, p. 115.
92. H. Fuji and H. Nakae, Acta
Metall. Mater., 44 (9) (1996), p. 3567.
93. P. Sebo, S. Kavecky, and P. Stefanik, J. Mater. Sci.
Lett., 13 (1994), p. 592.
94. V. Laurent, D. Chatain, and N. Eustathopoulos, Mater.
Sci. Eng., A135 (1991), p. 89.
95. C. Marumo and J.A. Pask, J.
Mater. Sci., 12 (1977), p. 223.
96. L. Battezatti and A.L. Greer, Acta
Metall. Mater., 37 (1989), p. 1791.
97. B.J. Keene, Int. Mater. Revs., 38 (1993), p.
157.
98. Smithels, Metals Reference Book (1983), pp. 14-17.
99. In Ref. 29
100. E. Saiz and A.P. Tomsia, J.
Amer. Ceram. Soc., 81 (9) (1998), p. 2381.
101. D. Muscat and R.A.L. Drew, Metall.
Mater. Trans., 25A (1994), p. 2357.
102. Y. Gao et al., J.
Mater. Res., 10 (5) (1995), p. 1216.
103. S.M. DeVincent and G.M. Michael, Metall.
Trans., 24A (1993), p. 53.
104. C. Toy and W.D. Scott, J.
Amer. Ceram. Soc., 73 (1990), p. 97.
105. A. Meir, P.R. Chidambaram, and G.R. Edwards, Acta
Mater., 46 (12) (1998), p. 4453.
106. J. Narcisco et al., Metall.
Mater. Trans., 26A (1995), p. 983.
107. A. Alonso et al., Metall.
Trans., 24A, 1993, p. 1423.
108. S.Y. Oh, K.C. Russel, and J.A. Cornie, Metall.
Trans., 20A (1989), p. 533.
109. P.B. Maxwell et al., Metall.
Trans., 21B (1990), p. 475.
110. J.H. Ahn, N. Terao, and A. Berghezen, Scripta
Metall., 22 (1988), p. 793.
111. S.M. DeVincent, D.L. Ellis, and G.M. Michal, NASA
CR # 187087 (Washington, D.C.: NASA,
1991).
112. A. Mortensen and T. Wong, Metall.
Trans., 21A (1990), p. 2257.
113. T. Choh and T. Oki, Mater. Sci. Tech., 3 (1987),
p. 378.
114. T. Choh, R. Kammel, and T. Oki, Z. Metallk.,
78 (1987), p. 286.
115. H.K. Kim, H.K. Liou, and K.N. Tu, J.
Mater. Res., 10 (3) (1995), p. 497.
116. N. Eustathopoulos, Int. Metals Revs., 28 (4)
(1983), p. 189.
117. N. Eustathopoulos et al., J.
Mater. Sci., 9 (1974), p. 1233.
118. N. Eustathopoulos and L. Coudurier, J.
Adhes. Sci. Tech., 6 (3) (1992), p. 1011.
119. N. Eustathopoulos, D. Chatain, and L. Coudurier, Mater.
Sci. Eng., A 135 (1991), p. 83.
120. J.G. Li and H. Hausner, J.
Europ. Ceram. Soc., 9 (1992), p. 101.
121. T.R. Jonas, J.A. Cornie, and K.C. Russel, Metall.
Mater. Trans., 26A (1995), p. 1491.
122. L. Coudurier and N. Eustathopoulos, J.
Mater. Sci., 24 (1989), p. 1109.
123. V. Laurent, D. Chatain, and N. Eustathopoulos, J.
Mater. Sci., 22 (1987), p. 244.
124. V. Laurent, D. Chatain, and N. Eustathopoulos, Mater.
Sci. Eng., A135 (1991), p. 89.
125. V. Laurent et al., Cast Reinforced Metal Composites,
ed. S.G. Fishman and A.K. Dhingra (Materials Park, OH: ASM,
1988), p. 27.
126. V. Laurent et al., Acta
Metall. Mater., 36 (1988), 1797.
127. D.J. Wang and S.T. Wu, Acta
Metall. Mater., 42 (12) (1994), p. 4029.
128. Z. Lijun et al., Interfaces in Metal-Ceramic Composites,
ed. R.Y. Lin et al. (Warrendale, PA: TMS,
1989), p. 213.
129. C.S. Kanetkar, A.S. Kacar, and D.M. Stefanescu, Metall.
Trans., 19A (1988), p. 1833.
130. D. Xu, D. Wang, and D. Lin, Scripta
Metall. Mater., 28 (1993), p. 599.
131. N. Eustathopoulos and B. Drevet, Compos. Interfaces,
2 (1) (1994), p. 29.
132. C. Rado, S. Kalogeropoulo, and N. Eustathopoulos,
Acta
Mater., 47 (2) (1999), p. 461.
133. A.M. Hadian and R.A.L. Drew, Mater.
Sci. Eng., A189 (1994), p. 209.
134. C. Iwamoto, M. Nomura, and S.I. Tanaka, in Ref.
29, p. 106.
135. M. Nomura, C. Iwamoto, and S.I. Tanaka, in Ref.
29, p. 23.
136. M. Nomura, C. Iwamoto, and S.I. Tanaka, Acta
Mater., 47 (2) (1999), p. 407.
137. A. Tsoga, A. Naomidis, and P. Nikolopoulos, Acta
Mater., 44 (9) (1996), p. 3679.
138. P. Xiao and B. Derby, Acta
Mater., 46 (10) (1998), p. 3491.
139. A. Meir, P.R. Chidamabaram, and G.R. Edwards, J.
Mater. Sci., 30 (1995), p. 3791.
140. A.D. Panasyuk, I.P. Neshpor, and L.I. Struk, Powd.
Met. & Metal Ceram., 32 (11) (1993), p. 924.
141. J.E. Lazaroff, P.D. Ownby, and D.A. Weirauch, J.
Amer. Ceram. Soc., 78 (3) (1995), p. 539.
142. P.D. Ownby, K.W. Li, and D.A. Weirauch, J.
Amer. Ceram. Soc., 74 (6) (1991), p. 1275.
143. N. Sobczak et al., Inzynieria Materialowa (NR
4/1998), p. 754.
144. N. Sobczak et al., Proc. Int. Conf. Composites
Eng. (ICCE-3), ed. D. Hui, p. 111.
145. K. Nogi et al., Acta
Mater., 46 (7) (1998), p. 2305.
146. N. Sobczak et al., Proc. Int. Conf. Cast Composites
95'.
147. D. Chatain et al., J.
Amer. Ceram. Soc., 76 (6) (1993), p. 1568.
148. D.A. Weirauch and W.J. Krafick, Metall.
Trans., 21A (1990), p. 1745.
149. J.F. Silvain, J.C. Bihr, and J. Douin, Composites,
Part A, 29A (1998), p. 1175.
150. H. Ho and S. Wu, Mater.
Sci. Eng., A248 (1998), p. 120.
151. W. Jung et al., Metall.
Mater. Trans., 27B (1996), p. 51.
152. S. Hara, M. Okamoto, and T. Tanaka, in Ref.
29, p. 94.
153. N. Sobczak et al., in Ref. 29,
p. 138.
154. V.S. Zhuravlev et al., in Ref. 29,
p. 158.
155. N. Sobczak et al., in Ref. 29,
p. 145.
156. E. Benko et al., in Ref. 29,
p. 100.
157. Y.V. Naidich, V. Zhuravlev, and K. Krasovskaya, Mater.
Sci. Eng., A245 (1998), p. 293.
158. H. Fuji et al., J.
Mater. Sci., 34 (1999), p. 3165.
159. S. Lequeux et al., in Ref. 29,
p. 112.
160. S.W. Ip et al., Mater.
Sci. Eng., A244 (1998), p. 31.
161. N. Frumin et al., Scripta
Mater., 37 (8) (1997), p. 1263.
162. P.R. Chidambaram, A. Meir, and G.R. Edwards, Mater.
Sci. Eng., A206 (1996), p. 249.
163. E. Saiz, A.P. Tomsia, and R.M. Cannon, Acta
Mater., 46 (7) (1998), p. 2349.
164. O. Dezellus and N. Eustathopoulos, Scripta
Mater., 40 (11) (1999), p. 1283.
165. K. Landry, C. Rado, and N. Eustathopoulos, Metall.
Mater. Trans., 27A (1996), p. 3181.
166. V. Laurent, C. Rado, and N. Eustathopoulos, Mater.
Sci. Eng., A205 (1996), p. 1.
167. V.M. Perevertailo, A.A. Smekhnov, and O.B. Loginova,
in Ref. 29, p. 127.
168. A.P. Tomsia et al., in Ref. 29.
169. N. Sobczak, Interfacial Science in Ceramic Joining,
ed. A. Bellosi, T. Kosmac, and A.P. Tomsia, NATO ASI Series, High Technology-vol
58 (Dordrecht, Netherlands: Kluwer
Academic Publishers, 1997), p. 27.
170. N. Grigorenko et al., in Ref. 29,
p. 27.
171. F.G. Yost, P.A. Sackinger, and E.J. O'Toole, Acta
Mater., 46 (7) (1998), p. 2329.
172. J.A. Warren, W.J. Boettinger, and A.R. Roosen, Acta
Mater., 46 (9) (1998), p. 3247.
173. R. Asthana, "Dissolutive Capillary Penetration with
Expanding Pores and Transient Contact Angles," J.
Colloid Interface Sci. (December 1999, submitted).
174. R. Asthana, "An Analysis for the Capillary Rise of
Reactive Melts," Metall.
Mater. Trans. (in press).
175. W.A. Zisman, Advances in Chemistry, 43 (1964),
p. 1.
176. E. Ricci and A. Passerone, Mater.
Sci. Eng., A161 (1993), p. 31.
177. N. Sobczak, Trans. Foundry Research Institute,
XLIV (4) (1994), p. 221.
178. J.F. Mcdonald and J.G. Eberhart, Trans. AIME,
233 (1965), p. 512.
179. A.W. Neumann et al., J.
Colloid Interface Sci., 49 (2) (1974), p. 291.
180. S.N. Omenyi and A.W. Neumann, J.
Appl. Phys., 47 (9) (1976), p. 3956.
181. S.N. Omenyi, R.P. Smith, and A.W. Neumann, J.
Colloid Interface Sci., 75 (1) (1980), p. 117.
182. D. Li and A.W. Neumann, J.
Colloid Interface Sci., 137 (1) (1990), p. 304.
183. D.M. Stefanescu et al., Metall.
Trans., 21A (1990), p. 231.
184. R. Asthana, Metall.
Mater. Trans., 25A (1994), p. 225.
185. R. Asthana, J.
Colloid Interface Sci., 165 (1994), p. 256.
186. E. Moy and A.W. Neumann, J.
Colloid Interface Sci., 119 (1) (1987), p. 296.
187. T.G.M. Van de Ven, J.
Colloid Interface Sci., 102 (1) (1984), p. 301.
188. T.G.M. Van de Ven et al., J.
Colloid Interface Sci., 91 (1) (1983), p. 297.
189. R.J. Good, J.
Colloid and Interface Sci., 59 (1977), p. 398.
190. S. Wu,
J. Colloid Interface Sci., 71 (3) (1979), p. 605.
191. S.K. Rhee, Mater.
Sci. Eng., 16 (1974), p. 45.
192. S.K. Rhee, J.
Amer. Ceram. Soc., 54 (8), p. 376.
193. R. Warren, J.
Mater. Sci., 15 (1980), p. 2489.
194. A.R. Miedema and R. Boom, Z. Metallkde., 69
(1978), p. 183.
195. A.R. Miedema and F.J.A. de Broeder, Z. Metallkde.,
70 (1979), p. 14.
196. E.M. Washburn, Phys. Rev., 17 (1921), p. 374.
197. G.P. Martins, D.L. Olson, and G.R. Edwards, Metall.
Trans., 19B (1988), p. 95.
198. K.A. Semlak and F.N. Rhines, Trans. AIME, 21
(1958), p. 325.
199. R. Asthana, Solidification Processing of Reinforced
Metals (Switzerland: Trans
Tech Publications, 1997), pp. 421.
200. R.P. Messner and Y-.M. Chiang, J.
Amer. Ceram. Soc., 73 (5) (1990), p. 1193.
201. V.N. Eremenko and L.D. Lesnik, The Role of Surface
Phenomena in Metallurgy, ed. V.N. Eremenko (New York: Consultant Bureau,
English Translation), p. 102.
202. R. Asthana, "An Analysis for the Capillarity Penetration
Kinetics in Reactive Couples" (Paper to be presented at the 2000
TMS Annual Meeting, Nashville, TN, 12-16 March, 2000).
203. R. Asthana and S.N. Tewari, Compos. Manuf.,
4 (1) (1993), p. 3.
204. K. Nogi and K. Ogino, Adv. Structural Materials,
ed. D.S. Wilkinson (New York: Pergamon, 1988), p. 97.
205. M. Shimbo, M. Naka, and I. Okamoto, J. Mater. Sci.
Lett., 8 (1989), p.663.
206. R. Warren and C.H. Anderson, Composites, 15
(1984), p. 101.
207. W. Kohler, Aluminium, 51 (1975), p. 443.
208. D.S. Han, H. Jones, and H.V. Atkinson, J.
Mater. Sci., 28 (1993), p. 2654.
209. J. Narcisco et al., Scripta
Metall. Mater., 31 (11) (1994), p. 1495.
210. R. Asthana and P.K. Rohatgi, Compos. Manuf.,
3 (2) (1992), p. 119.
211. R. Asthana and P.K. Rohatgi, Z. Metallkde.,
83 (12) (1992), p. 887.
212. B.M. Gallois, JOM,
49 (6) (1997), p. 48.
213. A.C.D. Chaklader, A.M. Armstrong, and S.K. Mishra,
J. Amer. Ceram.
Soc., 51 (11) (1968), p. 630.
214. A.C.D. Chaklader, W.W. Gill, and S.P. Mehrotra, Interfaces
in Ceramics.
215. J.J. Brennan and J.A. Pask, J.
Amer. Ceram. Soc., 51 (10) (1968), p. 569.
216. J.A. Champion, B.J. Keene, and J.M. Silwood, J.
Mater. Sci., 4 (1969), p. 39.
217. J. Goicoechea et al., Scripta
Metall. Mater., 25 (1991), p. 479.
218. R.D. Carnaham, T.L. Johnson, and C.H. Li, J.
Amer. Ceram. Soc., 41 (958) p. 343.
219. Y.V. Naidich et al., Poroshkovaya Metallurgiya,
246 (6) (1983), p. 67.
220. P.J. Bunyan and S.H. Huo, Advanced Composites '93,
ed. T. Chandra and A.K. Dhingra (Warrendale, PA: TMS,
1993), p. 1009.
221. E. Saez and A.P. Tomsia, J.
Amer. Ceram. Soc., 81 (9) (1998), p. 2381.
222. W.G. Fahrenholtz et al., Ceramic Microstructure:
Control at the Atomic Level, ed. A.P. Tomsia and A. Glaeser (New York: Plenum
Press, 1988), p. 749.
223. R.E. Loehman, K.G. Ewsuk, and A.P. Tomsia, J.
Amer. Ceram. Soc., 79 (1) (1996), p. 27.
224. K. Fujita, Y. Sawada, and K. Honjo, J. Jpn. Soc.
Compos. Mater., 17 (2) (1991), p. 80.
225. P. Rocher, J.M. Quenisset, and R. Naslain, J. Mater.
Sci. Lett., 4 (1985), p. 1527.
226. I.L. Kalnin, U.S. patent 4,056,874 (1977).
227. A.P. Levitt, E. DiCesare, and S.M. Wolf, Metall.
Trans., 3 (1972), p.2455.
228. R.T. Pepper and E.G. Kendall, U.S. patent 4,082,864
(1978).
229. O. Remondier et al., Developments in Sci. & Tech.
of Compos. Mater. (ECCM-I), ed. A.R. Bunsell et al., p. 732.
230. J.P. Rocher et al., Memoires et etudes Scientifiques
Revue de Metallurgie (February 1986), p. 69.
231. U. Gangopadhyaya and P. Wynblatt, J.
Mater. Sci., (1995), p. 94.
232. T.J. Whalen and A.T. Anderson, J.
Amer. Ceram. Soc., 58 (9) (1975), p. 396.
233. C. Zhongyu, W. Jimbo, and H. Xiangui, Interfaces
in Metal Ceramic Composites, ed. R.Y. Lin et al. (Warrendale, PA: TMS,
1988), p. 233.
234. N. Sobczak et al., Materials Science Forum,
Part I, 217-222, p. 153.
235. M. Nicholas and D. Mortimer, Proc. Int. Conf. Carbon
Fibers, Their Compos. and Applic. (London: Plastics Institute, 1971), p.
129.
236. K. Nogi, Y. Osugi, and K. Ogino, J. Iron Steel
Inst. Japan (ISIJ), 30 (1) (1990), p. 64.
237. W.B. Hillig et al., Ceram. Bull., 54 (1975),
p. 1054.
238. M.C. Breslin et al., Ceram. Eng. Sci. Proc.,
15 (4) (1994), p. 104.
239. F.P. Chiaramonte and B.N. Rosenthal, J.
Amer. Ceram. Soc., 74 (3) (1991), p. 658.
240. H. Fuji, H. Nakae, and K. Okada, Acta
Metall. Mater., 41 (10) (1993), p. 2963.
241. A.D. Panasyuk, I.P. Neshpor, and L.I. Struk, Powd.
Met. Metal Ceram., 32 (11/12) (1993), p. 924.
242. C.R. Manning and T.B. Gurganus, J.
Amer. Ceram. Soc., 52 (1969), p. 115.
243. S.W. Ip, M. Kuchanski, and J.M. Toguri, J. Mater.
Sci. Lett., 12 (1993), p. 1699.
244. N. Kishaporov et al., Sov. Powd. Met. Metal Ceram.,
11 (1984), p. 869.
245. K. Kobashi and T. Choh, J.
Mater. Sci., 28 (3) (1993), p. 684.
246. H. John and H. Hausner, J. Mater. Sci. Lett.,
5 (1986), p. 549.
247. H. Katzman, U.S. patent 4,376,803 (1983).
248. H. Katzman, J.
Mater. Sci., 22 (1987), p. 144.
249. B. Kindl et al., Composite Sci. Tech., 43 (1)
(1992), pages.
250. M. Entezarian and R.A.L. Drew, Mater.
Sci. Eng., A212 (1996), p. 206.
251. N. Sobczak et al., Proc. Third Conf. Surface Phenomena
in Foundry Processes (Poznan-Kolobrzeg, Poland, 1996), p. 193.
252. N. Sobczak et al., in Ref. 251,
p. 201.
253. N. Sobczak, unpublished data (1999).
254. N. Sobczak et al., Proc. Annual Meeting of American
Vacuum Soc. (New York: AVS,
1995).
255. N. Sobczak et al., to be published in J. Foundry
Research Institute (Poland).
256. N. Sobczak, Proc. Int. Conf. Light Alloys and Composites
(Zakopane, Poland, 1999), p. 341.
257. N. Sobczak et al.,in Ref. 251,
p. 193.
258. B.J. Dalgleish et al., Scripta
Metall., 31 (8) (1994), p. 1109.
259. J.T. Klomp, MRS Symp. Proc., 40 (Pittsburgh,
PA: MRS, 1985), p. 381.
260. R. Asthana, J.
Mater. Sci., 33 (1998), p. 1959.
261. R. Asthana, R. Tiwari, and S.N. Tewari, Metall.
Mater. Trans., 26A (1995), p. 2175.
262. S.N. Tewari et al., Metall.
Mater. Trans., 26A (1995), p. 477.
263. J.M. Howe, Int. Mater. Revs., 38 (5) (1993),
p. 233.
264. M. Ueki, M. Naka, and I. Okamoto, J. Mater. Sci.
Lett., 5 (1986), p. 1261.
265. M. Nicholas, P.R.D. Forgan, and D.M. Poole, J.
Mater. Sci., 3 (1968), p. 9.
266. M. Nicholas, J.
Mater. Sci., 5 (1970), p. 571.
267. P.K. Rohatgi et al., Mater.
Sci. Eng., A162 (1993), p. 163.
268. A.G. Evans et al., Mater.
Sci. Eng., A126 (1990), p. 53.
269. A.G. Evans et al., Metall.
Trans., 21A (1990), p. 2419.
270. F. Ernst, Mater.
Sci. Eng., R14 (1995), p. 97.
271. R. Asthana, S.N. Tewari, and S.L. Draper, Metall.
Trans. A, 29A (1998), p. 1527.
272. T.P.D. Rajan, R.M. Pillai, and B.C. Pai, J.
Mater. Sci., 33 (1998), p. 3491.
273. R.E. Baier, E.G. Shafrin, and W.A. Zisman, Science,
162 (1968), p. 1360.
Rajiv Asthana is an associate professor of manufacturing engineering in the Technology Department at University of Wisconsin-Stout. Natalia Sobczak is head of the Laboratory for Physical Chemistry of Metals and Alloys at the Foundry Research Institute in Krakow, Poland.
For more information, contact R. Asthana, University of Wisconsin at Stout,
Manufacturing Engineering, Technology Department, 326 Fryklund Hall, Menomonee,
Wisconsin 54751; (715) 232-2152; fax (715) 232-1330; e-mail asthanar@uwstout.edu.
| Search | TMS Document Center | Subscriptions | Other Hypertext Articles | JOM | TMS OnLine |
|---|