TMS ONLINE | TMS PUBLICATIONS | SITE MAP An Article from the June 2003 JOM: A Hypertext-Enhanced Article

VISIT THE JOM COVER GALLERY JOM MENU

Overview: Welding

Welding: Solidification and Microstructure

S.A. David, S.S. Babu, and J.M. Vitek

---

Figure 1. A schematic diagram showing the interaction between the heat source and the base metal. Three distinct regions in the weldment are the fusion zone, the heat-affected zone, and the base metal.

Figure 2. The calculated fluid-flow pattern in a stainless-steel stationary arc weld pool 25 s after the initiation of the arc.

Parameters that control the solidification of castings also control the solidification and microstructure of welds. However, various physical processes that occur due to the interaction of the heat source with the metal during welding add a new dimension to the understanding of the weld pool solidification. Conventional theories of solidification over a broad range of conditions can be extended to understand weld pool solidification. In certain cases, because of rapid cooling rate effects, it is not unusual to observe nonequilibrium microstructures. Recent developments in the application of computational thermodynamics and kinetic models, studies on single-crystal welds, and advanced in-situ characterization techniques have led to a better understanding of weld solidification and microstructures.

INTRODUCTION

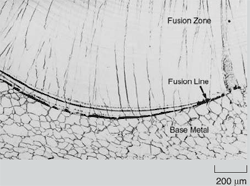
In welding, as the heat source interacts with the material, the severity of thermal excursions experienced by the material varies from region to region, resulting in three distinct regions in the weldment (Figure 1). These are the fusion zone (FZ), also known as the weld metal, the heat-affected zone (HAZ), and the unaffected base metal (BM). The FZ experiences melting and solidification, and its microstructural characteristics are the focus of this article.

The microstructure development in the FZ depends on the solidification behavior of the weld pool. The principles of solidification control the size and shape of the grains, segregation, and the distribution of inclusions and porosity. Solidification is also critical to the hot-cracking behavior of alloys. Sometimes, it is convenient to consider the FZ as a minicasting. Therefore, parameters important in determining microstructures in casting, such as growth rate (R), temperature gradient (G), undercooling (DT), and alloy composition determine the development of microstructures in welds as well. Comprehensive reviews of weld pool solidification based on these parameters are available in the literature.^1,2

Most knowledge of weld pool solidification is derived from the extrapolation of the knowledge of freezing of castings, ingots, and single crystals at lower thermal gradients and slower growth rates.^1–6 In addition, rapid solidification theories have been extended to welds solidified at very high cooling rates.^7–14However, microstructure development in the FZ is more complicated^15,16because of physical processes that occur due to the interaction of the heat source with the metal during welding, including re-melting, heat and fluid flow, vaporization, dissolution of gasses, solidification, subsequent solid-state transformation, stresses, and distortion. These processes and their interactions profoundly affect weld pool solidification and microstructure. In recent years, phenomenological modeling of welding processes has provided unprecedented insight into understanding both the welding process and the welded materials. A variety of sophisticated models that employ analytical and numerical approaches are capable of describing many physical processes that occur during welding.^15–25

During the past 15 years, significant progress has been made in understanding the solidification behavior of the weld pool and the evolution of microstructure in the FZ. The application of computational thermodynamic and kinetic tools has enhanced the understanding of weld solidification behavior of complex multi-component systems. Advanced in-situ characterization techniques have enabled the characterization of phase formation and non-equilibrium effects during weld pool solidification. The use of model alloy single crystals resulted in new insight into the role of weld pool geometry and dendrite growth selection processes in the development of weld microstructure. This overview will address some of the current progress in understanding weld pool solidification.

WELD POOL SHAPE

An important aspect of weld solidification is the dynamics of weld pool development and its steady-state geometry. Weld pool shape is important in the development of grain structure and dendrite growth selection process.^{6, 26-29}Thermal conditions in and near the weld pool and the nature of the fluid flow have been found to influence the size and shape of the weld pool.^{16–18,24,25}Significant advances have been made in recent years to understand, in greater detail, the dynamics of the heat and fluid flow in the weld and the subsequent development of the pool shape. To a large extent, convective flow in the weld pool determines weld penetration. For arc-welding processes, convection in the weld pool is mainly controlled by buoyancy, electromagnetic forces, and surface-tension forces. In actuality, depending on the interplay between various driving forces, the convective flow could be simple or more complex with a number of convective cells operating within the weld pool, as shown in Figure 2.

Recent theoretical developments include the formulation of a free-surface computational model to investigate coupled conduction and convection heat-transfer models to predict not only weld pool geometry but also thermal profiles to estimate thermal gradients and cooling rates critical to determining solidification structure.²⁵ In addition to computational models, neural net models have been applied to predict weld pool geometry.³⁰ These models, which are empirical in nature, are useful when applied to complex welding processes such as hybrid laser-arc welding.³⁰

MICROSTRUCTURE

Unlike in casting, during welding, where the molten pool is moved through the material, the growth rate and temperature gradient vary considerably across the weld pool. Geometrical analyses have been developed that relate welding speed to the actual growth rates of the solid at various locations in the weld pool.^1,2,27

Along the fusion line the growth rate is low while the temperature gradient is steepest. As the weld centerline is approached, the growth rate increases while the temperature gradient decreases. Consequently, the microstructure that develops varies noticeably from the edge to the centerline of the weld. Most of these microstructural features can be interpreted by considering classical theories of nucleation and growth.

In welds, weld pool solidification often occurs without a nucleation barrier. Therefore, no significant undercooling of the liquid is required for nucleation of the solid. Solidification occurs spontaneously by epitaxial growth on the partially melted grains. This is the case during autogenous welding. In certain welds, where filler metals are used, inoculants and other grain-refining techniques are used in much the same way as they are in casting practices. In addition, dynamic methods for promoting nucleation such as weld-pool stirring and arc oscillation have been used to refine the weld metal solidification structure.² Although the mechanisms of nucleation in weld metal are reasonably well understood, not much attention is given to modeling this phenomenon. Often, weld solidification models assume epitaxial growth and for most of the cases the assumption seems to be appropriate. However, to describe the effects of inoculants, arc oscillations, and weld pool stirring, heat and mass transfer models^18,24,25 have to be coupled with either probabilistic models such as cellular automata^31–33or deterministic models using the fundamental equations of nucleation as described elsewhere.³⁴

Figure 3. A scanning-electron micrograph showing the development of dendrites in a nickel-based superalloy single-crystal weld.		Figure 4. An optical micrograph shows the change in dendrite morphology from cellular to dendritic as the growth velocity increases toward the center of spot weld (from bottom to top) after the spot weld arc is extinguished.

During growth of the solid in the weld pool, the shape of the solid-liquid interface controls the development of microstructural features. The nature and the stability of the solid-liquid interface is mostly determined by the thermal and constitutional conditions (constitutional supercooling) that exist in the immediate vicinity of the interface.^35,36 Depending on these conditions, the interface growth may occur by planar, cellular, or dendritic growth. Dendritic growth of the solid, with its multiple branches, is shown in Figure 3. Another example of changes in solidification morphology directly related to welding conditions is shown in Figure 4. This figure shows a spot weld on a nickel-based superalloy in which the morphology changes from cellular to dendritic as the growth velocity increases toward the center of the spot weld after the spot weld arc is extinguished. The micrograph also shows the elimination of a poorly aligned dendrite, which is discussed in greater detail later. The criterion for constitutional supercooling for plane front instability can be mathematically stated as:

plane front will be stable

(1)

planar instability will occur

(2)

where G_L is the temperature gradient in the liquid, R is the solidification front growth rate, DT_O is the equilibrium solidification temperature range (at composition C_O), and D_L is the solute diffusion coefficient in liquid.

Figure 5. Epitaxial and columnar growth near the fusion line in an iridium alloy electron-beam weld. The figure also shows the grain-growth selection process of the grains from the fusion line.

Solute distribution during weld pool solidification is an important phenomenon resulting in segregation that can significantly affect weldability, microstructure, and properties. Studies extending different solidification models to describe solute distribution during weld solidification are summarized elsewhere.² In describing the solute distribution under dendritic growth conditions, consideration should be given to redistribution at the dendrite tip and in the interdendritic regions. In welds, since the microstructures are much finer in scale than in castings, the contribution to the total tip undercooling due to the curvature effect is significant.² The effect of increased undercooling at the dendrite tip would be to solidify at a composition closer to the overall composition and thus reduce the extent of microsegregation. Dendrite tip undercoolings in welds have been estimated by measuring dendrite core compositions for Al-Cu and Fe-Nb systems after welding.³⁸ For solute distribution in the interdendritic regions it may be sufficient to extend the solidification models for microsegregation in castings to welds. This can be achieved by the Schiel equation³⁹ or modified Schiel equation that considers the diffusion in the solid during welding.^38,40

As mentioned earlier, since solidification of the weld metal proceeds spontaneously by epitaxial growth of the partially melted grains in the base metal, the FZ grain structure is mainly determined by the base metal grain structure and the welding conditions.² Crystallographic effects will influence grain growth by favoring growth along particular crystallographic directions, namely the easy growth directions.^35,36,41 For cubic metals, these easy directions are <100>. Which of these <100> directions will be selected, a fundamental question that is important when welding single crystals, will be addressed later. Conditions for growth are optimum when one of the easy growth directions coincides with the heat-flow direction. Thus, among the randomly oriented grains in a polycrystalline specimen, those grains that have one of their <100> crystallographic axes closely aligned with heat-flow direction will be favored. Without additional nucleation, this will promote a columnar grain structure. Figure 5 shows clearly the grain growth selection process in an iridium alloy weld. Under certain conditions it is also possible to change the epitaxial columnar growth to equiaxed growth by inoculation or changing welding conditions.^28,42,43

SOLIDIFICATION OF SINGLE-CRYSTAL WELDS

Studies on Fe-15Ni-15Cr single-crystal welds carried out during the last ten years have advanced significantly the fundamental understanding of weld pool solidification.^27–29 These studies have identified the effect of crystallography on the development of FZ microstructure. A geometrical model has been developed that provides a three-dimensional relationship between travel speed, solidification velocity, and dendrite growth velocity that predicts stable dendrite growth directions as a function of weld pool shape and weld orientation. The regions of differently oriented dendrites develop because growth occurs along the preferred <100> growth directions, and the choice of which growth direction will prevail among the six possible variants is based on the relation between weld pool shape and dendrite orientation. The model’s capability to predict microstructural features in an Fe-15Ni-15Cr singlecrystal electron beam weld made along [100] on (001) plane is shown in Figures 6a and 6b.

Recently, these basic concepts have been extended to commercial nickel-based superalloy single-crystal technology technology used in jet and land-based turbine engines.^44–46 Unlike in Fe-15Ni-15Cr single-crystal welds where the single crystallinity of the weld was maintained, nickel-based superalloys are extremely prone to stray grain formation (as shown in Figure 7). This phenomenon can be attributed to constitutional supercooling^46,47or dendrite fragmentation⁴⁸ ahead of the dendritic front that may nucleate new grains. Recent studies suggest that the constitutional supercooling may be the controlling mechanism for straygrain formation.^44,47

a		b
Figure 6. (a) An Fe-15Cr-15Ni single-crystal electron-beam weld made along [100] direction on (001) plane, and (b) the calculated dendritic growth pattern for a similar weld orientation in (a).				Figure 7. An optical micrograph of overlapping laser spot welds on PWA-1480 single-crystal nickel-based superalloy showing the formation of stray grains at the center of the weld.

NONEQUILIBRIUM SOLIDIFICATION

Because of the rapid cooling rates encountered during welding, especially during high-power-density processes such as electron and laser-beam welding, it is not uncommon to observe nonequilibrium solidification effects. Most nonequilibrium features in welding can be associated with two phenomena that take place as the solidification growth velocities increase. First, the partitioning of solute between solid and liquid, described by the partitioning coefficient k (= solid composition/liquid composition, both at the solid/liquid interface), is affected by growth rate such that, as the growth velocity increases, k deviates from the equilibrium value and approaches a value of 1. Second, high growth velocities can lead to a change in the solidification mode and result in nonequilibrium phase formation. It is noteworthy that these phenomena are closely interrelated.

As discussed earlier, the solidification morphology also changes with growth velocity and is influenced by the extent of solute partitioning and the phase that forms. In this section, nonequilibrium solute partitioning will be addressed, but even equilibrium solute partitioning can lead to nonequilibrium phase formation because of residual microsegregation; this can be evaluated by the Scheil equation and its variants.

a		b
Figure 8. Photomicrographs of high-speed laser welds showing (a) fully ferritic microstructure in type-312 stainless steel with negligible secondary austenite formation and (b) nonequilibrium austenitic microstructure in type-308 stainless steel without any ferrite formation.

Theories have been developed to relate the degree of partitioning to the growth rate.¹⁴ For high growth rates that may be prevalent during welding, reduced solute partitioning resulting from a change in k can lead to a variety of effects including morphological changes to plane front solidification, changes in the solidification phase, and less segregation in the weld microstructure. An example is shown in Figure 8a, where an autogenous laser weld was made on a 312 stainless-steel weld overlay pad. The laser-weld microstructure is fully ferritic, which reflects the fact that minimal partitioning during solidification prevented secondary austenite formation, as found in the weld overlay. In this case, the rapid cooling conditions during laser welding also prevented solid-state transformation of the solidified ferrite to austenite.

Numerous examples of nonequilibrium solidification in austenitic stainless steels have been documented over the years.^8–11,49 An example is shown in Figure 8b. In this case, the micrograph is of an autogenous laser weld on a 308 stainless-steel weld overlay. The base material (weld overlay), shown on the left, shows the typical weld microstructure in this material consisting of austenite and residual ferrite. This is produced by primary ferrite solidification followed by secondary austenite solidification and ferrite transformation to austenite during solid-state cooling. The laser-weld microstructure is completely different. It is a fully austenitic microstructure produced by nonequilibrium primary austenite solidification.

Another example of nonequilibrium solidification in a low-alloy steel is presented in the section on in-situ observations. It is also noteworthy that the laser-welded microstructure does not show any dendritic structure; this is another example of the solidification morphology changing to planar solidification at high growth rates. Extremely high growth rates are not necessary to produce nonequilibrium solidification. A series of experiments in which welds were made across dissimilar stainless steels showedthat nonequilibrium solidification can be found even under less extreme solidification conditions.⁵⁰ Current research focuses on the quantitative prediction of these transitions from equilibrium to nonequilibrium conditions by numerical modeling of weld solidification in multicomponentalloys.

MODELING WELD SOLIDIFICATION

In addition to heat and fluid-flow models used for welding, additional modeling techniques are now available that can help describe the phase evolution during weld solidification. Foremost among these are computational thermodynamic models for multicomponent systems that can predict the primary solidification phases, the solidification phases that may form as a result of solute partitioning during solidification, and the stability of these phases as the weldments are cooled to room temperature. For example, one such program, ThermoCalc,⁵¹ has been used to calculate a phase diagram for a hypothetical Fe-20Cr-8Ni-xN (wt.%) alloy as a function of temperature and chromium content for two different nitrogen concentrations, x = 0.01% and x = 0.1% (Figure 9a and Figure 9b, respectively). The plots show that at 20% chromium, for both 0.01% nitrogen and 0.1% nitrogen, the primary solidification will occur by d-ferrite. However, the phase stability following solidification is quite different. In the case of the low-nitrogen stainless steel, at 800°C, a mixture of ferrite and austenite is expected while a fully austenitic structure is predicted for the high-nitrogen alloy in equilibrium at the same temperature. Such calculations are simple and can be used to identify the effect of alloy composition on the phase stability during and after weld solidification. Perhaps the greatest benefit that results from these models is that the calculations can be performed easily for complex multicomponent systems with ten or more constituents.

Kinetics models based on diffusion-controlled growth can be integrated with computational thermodynamics models to provide valuable information on the time evolution of the microstructure.⁵² For example, in the case of welding, calculations can be made to identify the effect of cooling rate on the final microstructure.

Such calculations were made for the two Fe-20Cr-8Ni-xN alloys described above. The calculations assumed a half-dendrite arm spacing of 100 µm and a cooling rate of 10 Ks^–1. The model considered a peritectic solidification mode, with primary ferrite formation and secondary austenite formation at the ferrite/liquid interface. The results of the calculations are shown in Figure 9c and Figure 9d, where the phase fractions are plotted versus time. In the case of the high-nitrogen welds, the austenite growth into ferrite phase was found to increase rapidly after ~35 s. Thus, the diffusion-controlled growth models allow the calculation of the amount of d-ferrite that may be retained after solidification and the description of the weld microstructure evolution in stainless steels to a certain extent. These calculations can be repeated for different weld cooling rates and dendrite arm spacings to evaluate the effect of welding process parameters on the microstructure.

As noted in the previous section, nonequilibrium solidification may take place at higher cooling rates and solidification growth rates. Recent advances in interface-response function models⁵³ can be used to evaluate the phase selection during solidification in multicomponent steels by coupling them with computational thermodynamic software. The interface-response function model evaluates the dendrite tip radius, tip temperature, and partition coefficients as a function of interface velocity for various competing phases and determines which solidification phase is kinetically favored. The next step in the modeling of weld solidification is to couple computational thermodynamic, diffusion-controlled growth models, crystallographic geometry models,²⁷ and cellular automata⁵⁴ models to depict the fine details of microstructure morphology as a function of composition and welding process parameters.

a		b
c		d
Figure 9. Quasi-binary diagrams showing liquid, austenite, and d-ferrite phase regions in Fe-Cr-Ni alloy systems with (a) 0.01 wt.% nitrogen and (b) 0.1 wt.% nitrogen. The calculated variation of phase fraction as a function of cooling time from 1,750 K using a diffusion-controlled growth model for Fe-Cr-Ni alloy systems with (c) 0.01 wt.% nitrogen and (d) 0.1 wt.% nitrogen.

IN-SITU OBSERVATIONS

Modeling activities must be accompanied by careful experimental measurements in order to validate the models. Traditionally, the evaluations of models have been made by post-weld characterization of solidification microstructures using optical microscopy and analytical electron microscopy. However, interpretation of weld behavior by examination of welds at room temperature is often incomplete and complicated by phase transformations that take place upon cooling. There is a growing need to monitor solidification microstructure in-situ during weld cooling. Many techniques are currently available to observe the weld solidification features in-situ, including high-speed, high-resolution photography on real materials⁵⁵ or on metal analog transparent systems,³⁷ and time-resolved x-ray diffraction (TRXRD) with synchrotron radiation.⁵⁶

Recent results from metal analog transparent systems, combined with detailed numerical heat transfer models and solidification theories, led to the identification and analysis of instabilities at the liquid-solid interface while welding at high speeds.³⁷ Additional work has focused on nonequilibrium phase selection during weld solidification in an Fe-C-Al-Mn steel by means of in-situ observations using the TRXRD 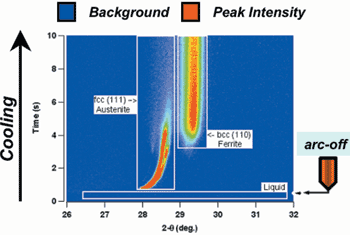technique.^57,58 In this research, the equilibrium primary solidification phase is d-ferrite and this was confirmed by TRXRD measurements on slowly cooled spot welds. However, under rapid cooling conditions, the TRXRD measurements showed the formation of primary austenite (Figure 10). Research in stainless steels has shown that it is possible to form nonequilibrium primary austenite under rapid solidification conditions but this is the first time such a phenomenon was observed in a low-alloy steel. In these steels, in-situ measurements are particularly valuable since behavior at elevated temperatures is masked by subsequent solid-state transformation of ferrite to austenite and austenite to martensite. Time-resolved x-ray diffraction measurements have proven to be ideal for identifying competing phase-transformation mechanisms under nonequilibrium weldcooling conditions. This technique has been applied to other alloy systems and exciting new insight into issues relating to weld solidification issues is being achieved.⁵⁹

Figure 10. An image representation of time-resolved x-ray diffraction data that shows the formation of primary austenite (fcc) from liquid during rapid cooling.

ACKNOWLEDGEMENTS

This research is sponsored by the Division of Materials Sciences and Engineering, Office of Basic Energy Sciences, U.S. Department of Energy, under Contract DE-AC05-00OR22725 with UT-Battelle, LLC.

References

1. W.F. Savage, Welding World, 18 (1980), p. 89.
2. S.A. David and J.M. Vitek, Inter. Mater. Review, 34 (5) (1989), p. 213.
3. G.J. Davies and J.G. Garland, Inter. Mater. Review, 20 (1975), p. 83.
4. F. Matsuda, T. Hashimoto, and T. Senda, Trans. Natl. Res. Inst. Met. (JPN), 11 (1) (1969), p. 83.
5. K.E. Easterling, Introduction to Physical Metallurgy of Welding (London: Butterworths, 1983).
6. S. Kou, Welding Metallurgy, Second edition (New York: John Wiley & Sons, Inc., 2002).
7. R. Mehrabian, Inter. Metall. Review, 27 (1982), p. 185.
8. J.M. Vitek, A. DasGupta, and S.A. David, Metall. Trans., 14A (1983), p. 1833.
9. S.A. David, J.M. Vitek, and T.L. Hebble, Weld J., 66 (1987), p. 289s.
10. S. Katayama and A. Matsunawa, Proc. of Int’l Congress on Application of Lasers and Electro Optics, vol. 4 (Boston, MA: Laser Institute of America, 1984), p. 60.
11. J.W. Elmer, S.M. Allen, and T.W. Eager, Metall. Trans. 20A (1989), p. 2117.
12. R. Trivedi and W. Kurz, Acta Metall. 34 (1986), p. 1663.
13. W.J. Boettinger and S.R. Coriell, Mater. Sci. Eng., 65 (1984), p. 27.
14. M.J. Aziz, J. Appl. Phys., 53 (1982), p. 1158.
15. S.A. David and T. DebRoy, Science, 257 (1992), p. 497.
16. T. DebRoy and S.A. David, Reviews of Modern Physics, 67 (1) (1995), p. 85.
17. S.A. David and T. DebRoy, MRS Bulletin, XIX (1) (1994), p. 29.
18. T. Zacharia et al., Metall. Trans., 20A (1989), p. 957.
19. K. Hong, D.C. Weckman, and A.B. Strong, Trends in Welding Research, ed. H.B. Smartt, J.A. Johnson, and S.A. David (Materials Park, OH: ASM Int., 1996), p. 399.
20. R.T.C. Choo and J. Szekely, Weld J., 73 (1994), p. 255.
21. W. Pitscheneder et al., Weld J., 75 (3) (1996), p. 71s.
22. Y. Dong et al., Weld J., 76 (10) (1997), p. 442s.
23. J. Goldak et al., Mathematical Modeling of Weld Phenomena 3, ed. H. Cerjak (London: Institute of Materials, 1997), p. 543.
24. T. DebRoy, Proceedings of the Julian Szekely Symposium on Materials Processing, ed. H.Y. Sohn, J.W. Evans, and D. Apelian (Warrendale, PA: TMS, 1997), p. 365.
25. T. DebRoy et al., Mathematical Modeling of Weld Phenomena 6, ed. H. Cerjak (London: Institute of Materials, 2002), p. 21.
26. S.A. David and C.T. Liu, Weld J., 61 (1982), p. 157s.
27. M. Rappaz et al., Metall. Trans. 20A (1989), p. 1125.
28. S.A. David et al., Metall. Trans. A, 21A, (1990), p. 1753.
29. J.M. Vitek et al., Int’l. Trends in Welding Science and Tech., ed. S.A. David and J.M. Vitek (Materials Park, OH: ASM Int., 1993), p. 167.
30. J.M. Vitek et al., Sci. Technol. Weld. Joining, 6 (5) (2001), p. 305.
31. B. Radhakrishnan and T. Zacharia, Modeling and Control of Joining Processes, ed. T. Zacharia (Miami, FL: Am. Weld. Soc., 1994), p. 298.
32. Ch.-A. Gandin, M. Rappaz, and R. Tintillier, Metall. Trans., 24A (1993), p. 467.
33. W.B. Dress, T. Zacharia, and B. Radhakrishnan, Modeling and Control of Joining Processes, ed. T. Zacharia (Miami, FL: Am. Weld. Soc., 1994), p. 321.
34. S.S. Babu et al., Mater. Sci. Technol., 11 (1995), p. 186.
35. M.C. Flemings, Solidification Processing (New York: McGraw Hill, 1974).
36. W. Kurz and D.J. Fisher, Fundamentals of Solidification (Aedermannsdorf, Switzerland: Trans-Tech. Publications, 1986).
37. R. Trivedi et al., J. Appl. Phys., 93 April (2003) p. 4,885.
38. J.A. Brooks and M.I. Baskes, Advances in Welding Science and Technology, ed. S.A. David (Materials Park, OH: ASM Int., 1986), p. 93.
39. E. Scheil, Z. Metall, 34 (1942), p 70.
40. T. Matsumiya et al., Nippon Steel Technical Report 57 (1993), p. 50.
41. W.F. Savage, C.D. Lundin, and A. Aronson, Weld J., 44 (1965), p. 175.
42. T. Ganaha, B.P. Pearce, and H.W. Kerr, Metall. Trans, 11A (1980), p. 1351.
43. H.W. Kerr and J.C. Villefuerta, Metal. Sci. of Joining, ed. K.J. Cieslak et al. (Warrendale, PA: TMS, 1991), p. 11.
44. J.M. Vitek et al., to be published in proceedings of Thermec 2003, (Switzerland: Trans Tech Publishers) Madrid, Spain.
45. S.A. David et al., Sci. Technol. Weld. Joining, 2 (2) (1997), p. 79.
46. J.M. Vitek, S.A. David, and L.A. Boatner, Sci. Technol. Weld. Joining, 2 (3) (1997), p. 109.
47. M. Gäumann, R. Trivedi, and W. Kurz; Mater. Sci. Eng., A 226-228 (1997), p. 763.
48. T.M. Pollock and W.H. Murphy, Metall. Mater. Trans., 27A (1996), p. 1081.
49. J.M. Vitek and S.A. David, Laser Materials Processing IV, ed. J. Mazumder, K. Mukherjee, and B.L. Mordike (Warrendale, PA: TMS 1994), p. 153.
50. H.K.D.H. Bhadeshia, S.A. David, and J.M. Vitek, Mater. Sci. Technol. 7 (1991) p. 50.
51. B. Sundman, B. Jansson, and J.O. Andersson, Calphad, 9 (1985) p. 1.
52. J. Agren, ISIJ International, 32 (1992), p. 291.
53. S. Fukumoto and W. Kurz, ISIJ International, 38 (1998), p. 71.
54. U. Dilthey, V. Pavlik, and T. Reichel, Mathematical Modeling of Weld Phenomena 3, ed. H. Cerjak (London: Institute of Materials, 1997) p. 85.
55. A.C. Hall et al., Proceedings of the 11th International Conference and Exhibition on Computer Technology in Welding (Columbus, Ohio, 2001).
56. J.W. Elmer, J. Wong, and T. Ressler, Metall. Mater. Trans., 29A (1998) p. 276.
57. S.S. Babu et al., J. Proc. Roy. Soc. A., 458 (2002), p. 811.
58. S.S. Babu et al., Acta Materialia, 50 (2002), p. 4763.
59. J.W. Elmer, T. Palmer, and S.S. Babu, Adv. Mater. Proc.,160 (2002) p. 23.

For more information, contact S.A. David, Oak Ridge National Laboratory, Metals & Ceramics Division, Building 4508, MS 6095, Oak Ridge, Tennessee 37831-6095; (865) 574-4804; fax (865) 574-4928; e-mail Davidsa1@ornl.gov.