 |
http://www.tms.org/pubs/journals/JOM/9704/Frazier/
|
 |
http://www.tms.org/pubs/journals/JOM/9704/Frazier/
|
| CONTENTS |
|---|
In this article, issues relating to modeling and simulating metal-forming equipment for the metals-processing industries are presented. Special emphasis is placed on the use of modern graphical simulation tools, and the application and experimental verification of the techniques as applied to a vertical hydraulic forge press located at Wright-Patterson Air Force Base are described.
INTRODUCTION
Motivating factors for the development of accurate models and computer simulations of metal-forming equipment are three-fold. First, the ability to quickly develop improved press control algorithms is greatly enhanced by the ability to perform repeated computer experiments without the need for costly and time-consuming experimental tests that can interfere with production. Second, as the use of finite-element modeling (FEM) techniques for the analysis and design of metal-forming processes continues to increase and become more sophisticated, the need to integrate accurate equipment models into the FEM-based simulations is increasing. Third, with the possibility of directly sensing workpiece conditions during forming operations, it is conceivable that these measurements could be fed back to the metal-forming equipment for computer control of the forming equipment, thereby enabling real-time compensation for variations in initial workpiece and equipment conditions.1 From a process control perspective, this approach should enable the highest level of robustness and repeatability in production. Common to each of these factors is the need for improved control and predictability of the equipment's behavior, which itself is based on the desire to achieve near-net shapes, higher-quality end products, higher yields, and better control of microstructure, especially for hard-to-form materials.
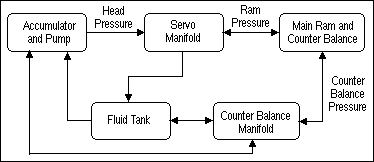 |
| Figure 1. A block diagram of a typical hydraulic forge press. The lines represent possible directions of fluid flow. |
THE COMPUTER SIMULATION OF DYNAMIC SYSTEMS
The use of a system model to predict the behavior of an actual system is desirable in many situations. In the case of design, the actual system may not yet exist, and it may be desirable to evaluate several possible configurations. In the case of analysis, an experiment on the actual system may take too much or too little time, may be too expensive, and may even damage the system—all undesirable situations. Still, many complex systems cannot be accurately described by mathematical models that can be evaluated analytically to obtain responses to a particular set of inputs or parameters. The simulation alternative consists of evaluating the model numerically with the inputs and parameters in question to determine how the outputs of interest are affected.10
Simulation techniques have been commonly used tools in the analysis and design of engineering systems for many years. In particular, the simulation of continuous-time and discrete-time dynamic systems has been the subject of vast research for several decades. Simulation languages such as the Continuous System Modeling Program (CSMP) and the Advanced Continuous Simulation Language (ACSL) have been specifically developed for building dynamic system simulation models.
The state of the art in the simulation of dynamic systems includes software packages that not only aid the engineer in building simulation models, but facilitate the creation of models and the interpretation of results by means of sophisticated graphical user interfaces. SIMULINK, VisSim, and MatrixX are three such packages.
A simulation model, in the sense used here, is represented by a block diagram in which all relevant elements and relationships that model the system are included. In the case of the forging system under consideration, which includes the forge press, the workpiece loading, and the internal mechanisms by which the microstructure of the workpiece evolves, the top level block diagram of a VisSim simulation model is shown in Figure 2. Each block in such a simulation diagram models an element or group of elements in the actual system, a data input port, or an output port. Each line represents a path for the flow of information or energy. Note in Figure 2 that the fundamental blocks in the forging process simulation are the forge press, the controller, and the tooling package. Each of these blocks comprises of several levels of subsystems, which can be observed with convenient editing tools in the graphical simulation environment.
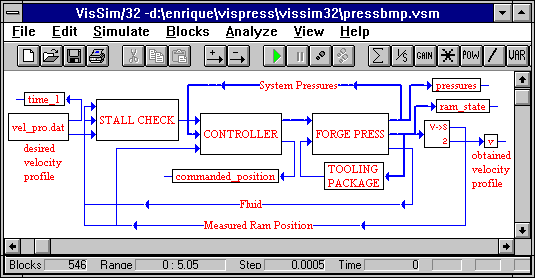 |
| Figure 2. A block diagram generated by VisSim. |
Generating Automatic Equipment-Simulation Code for Metal Forming
One objective underlying the work described here is to provide the metal-forming industry with scientifically based tools that will expedite design by allowing the user to perform what-if studies that include all aspects of the manufacturing process. For this reason, it is desirable to have a software module that will generate the response of the system to specific inputs without having to use a simulation package (i.e., a stand-alone program or a set of routines that will simulate the system without the need for a dedicated simulation software package on the part of the end user). This can be achieved by using the automatic-code-generation features available for any of the state-of-the-art simulation packages mentioned above.
The idea is to build the simulation model in one of the available simulation software packages and then generate a high-level language code that can be compiled to generate a program or library that will be used to simulate the system. The original simulation model can be developed by a consulting firm hired to deliver executable code or libraries for the simulation of the particular system. Such an executable code or library can then be used in conjunction with existing finite-element analysis software by the engineer in charge of the design to simulate the forging process .
APPLICATION TO THE ERIE 1000 TON FORGE PRESS
The Erie 1,000 ton forge press located at Wright-Patterson Air Force Base (WPAFB) is a vertical hydraulic forge press possessing a programmable, computer-based ram velocity control system employing hydraulic pressure and ram position feedback. The press was manufactured by Erie Corporation, Erie, Pennsylvania; the hydraulic control system was designed and built by Oilgear, Milwaukee, Wisconsin. The press has been in service since 1990 for performing manufacturing and metallurgical research at WPAFB. The power plant consists of an axial piston pump with 5.17 l/s capacity driven at 20 rps by an 149 W electric motor. Transient demands for higher flow rates are provided by a 60.57 liter hydraulic separator tank and a 738 liter nitrogen bottle. Nominal head pressure is 26.2 MPa. The maximum stroke of the ram is 38.1 cm and the maximum speed of the ram is approximately 12.7 cm/s. This maximum speed cannot be maintained over the entire stroke due to the limited capacity of the pump and size of the separator tank. The cross-sectional area of the main ram piston is 3813 cm2. The main ram is supported by two counter-balance pistons with cross-sectional areas of 186 cm2 each. The relief valve pressure on the counter-balance is 6.9 MPa. This implies that the counter-balance can support 257 kN. The nominal weight of the main ram is 187 kN.
The speed of the press is regulated by the use of two Oilgear three-way servovalves and one Parker proportional throttle valve. The gains of these valves are:
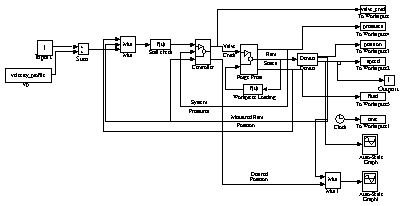 |
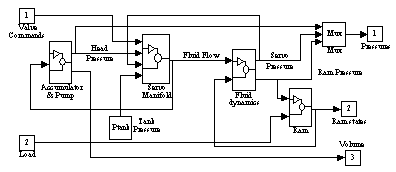 |
| Figure 3. SIMULINK block diagrams for (a—top) the press system and (b—bottom> the forge press. |
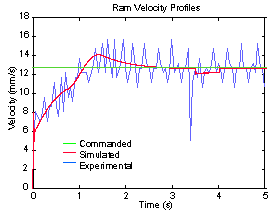
In order to verify that the computer model was accurate, experimental data from a simple forging were recorded and compared with the corresponding simulation data. The experimental forging was a cylindrical upsetting of plain carbon steel. The press was programmed to forge at a constant velocity of 1.27 cm/s. A plot of the experimental and simulated ram velocity is shown in Figure 4a. The irregularity in the experimental data of Figure 4a is due to the method used by the press computer to estimate the velocity. This behavior is not present in the actual press motion. Other than this effect, the simulation data closely resemble the experimental data. The data clearly reveal the ramping up and overshoot of the desired velocity. A brief change in velocity due to impact with the workpiece is observed near 3.5 seconds.
Figure 4b shows the experimental and simulated results for the ram load as derived from the ram pressure measurement. The plot reveals that approximately 88.96 kN are needed to overcome the counter-balance and frictional forces. The load increases rapidly beginning at approximately 3.5 seconds. This corresponds to impact with the workpiece. Beginning at approximately 4 seconds, elastic deformation of the workpiece and tooling ceases and plastic deformation of the workpiece begins. It is clear from the data that the press was able to maintain the desired velocity under load, as long as the load did not increase too rapidly.
 |
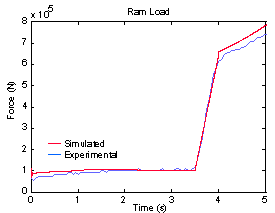 |
| Figure 4a. Ram velocity | Figure 4b. Ram load |
 |
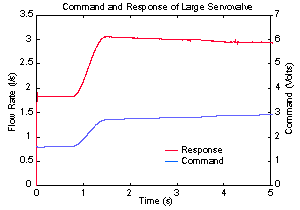 |
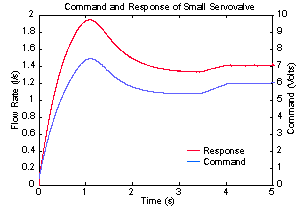
| Figure 5a. Small valve command and response | Figure 5b. Large valve command and response |
The press, computer does not record the commands to the hydraulic valves, but it is interesting to observe the plots of these commands and the corresponding valve flow rates from the simulation. These plots are shown in Figure 5. Notice that a particular valve command does not always result in the same flow rate. This is due to the changing pressure across the servo manifold, clearly revealing that the flow rate can decrease even as the command for higher velocity increases.
SIMULATION RESULTS FOR A SIMPLE PANCAKE FORGING
![]() A simple pancake forging process was simulated using the developed model. This model was validated against data obtained from a simple upset experiment.2
A simple pancake forging process was simulated using the developed model. This model was validated against data obtained from a simple upset experiment.2
As the animation progresses, note that when the hammer touches the workpiece, which occurs at roughly 3.5 seconds, the ram speed decreases for a very short time due to the load imposed. The control system immediately responds in order to drive the velocity back to its desired value of 1.25 cm/s. All changes in the ram velocity before 3.5 seconds are due solely to the dynamics of the press itself. Observe also that the load starts to increase as soon as the workpiece starts to deform. The regimes of elastic and plastic deformation can easily be identified by the different slopes in the load curve.
CONCLUSIONS
The use of graphics-based system modeling and simulation software greatly assists in making the modeling process systematic, self-documenting, accurate, and time efficient. The ability to quickly perform what-if experiments with regard to different control strategies, sensors, actuators, and tooling aids the engineer in making informed decisions regarding potential changes to existing metal-forming equipment and/or processing operations. For example, this approach makes it possible for the engineer to answer questions concerning the wisdom of possibly adding a sensor for the direct measurement of ram velocity for feedback control of the ram velocity as opposed to simply using pressure feedback. As the need for precise control of ram velocity, as well as position, increases, the need for direct measurement of velocity as a feedback control signal will become more acute. Current techniques for controlling velocity (inversion of servovalve flow models combined with pressure measurements and numerical differentiation of displacement measurements) are not adequate for high performance over a broad range of forging conditions.
Experience shows the need for press operators to customize the press control law in order to achieve the desired velocity profile for different forming operations. Having a custom control law for equipment that repeatedly makes the same part for several weeks or more is satisfactory, but as the need to use the same equipment for several different parts in a day or custom small lots increases, having to repeatedly tune the control law can waste significant time. Control laws need to be designed to be robust so that different loading conditions and velocity profiles can be handled successfully without the need for customized tuning.
It is anticipated that future work will include the use of the automatic code generation features in modern simulation packages to integrate accurate equipment models into finite-element simulation software to further improve the accuracy of simulated metal-forming processes.
ACKNOWLEDGEMENTS
This work was performed under the sponsorship of the Material Process Design Branch, Wright-Patterson Air Force Base, Ohio. The authors are thankful to Mr. Douglas R. Barker, of UES, Inc., and his colleagues in the Materials Processing Laboratory at WPAFB, for their assistance during the equipment modeling and experimental stages of this work.
References
1. W.M. Mullins, R.D. Irwin, S. Venugopal, and J.C. Malas (1996), "The Simulation of Acoustic Emission for Metal Forging," JOM, 48 (9) (1996), pp. 35-37.
2. W.G. Frazier, R.D. Irwin, E.A. Medina, and J.C. Malas, "Modeling and Simulation of Metalforming Equipment," submitted to the Journal of Materials Engineering and Performance.
3. S. Bennet and D.A. Linkens, Computer Control of Industrial Processes (New York: Peter Peregrinus, 1982).
4. Wayne Anderson, Controlling Electrohydraulic Systems (New York: Marcel Dekker, 1988).
5. Ernest E. Lewis and Hansjoerg Stern, Design of Hydraulic Control Systems (New York: McGraw-Hill, 1962).
6. Duone Tandeske, Pressure Sensors (New York: Marcel Dekker, 1991).
7. Harry N. Norton, Handbook of Transducers for Electronic Measuring Systems (Englewood Cliffs, New Jersey: Prentice-Hall, 1969).
8. P.E. Wellstead, Introduction to Physical System Modelling (New York: Academic Press, 1979).
9. Paul M. DeRusso, Rob J. Roy, and Charles M. Close, State-Variables for Engineers (New York: John Wiley and Sons, 1965).
10. Law and W.D. Kelton, Simulation Modeling and Analysis, 2nd ed. (New York: McGraw-Hill, 1991), pp. 1-6; 109-116.
For more information, contact W. Garth Frazier, Building 653, Wright Materials Laboratory, Wright-Patterson Air Force Base, Ohio 45433-7746; telephone (937) 491-4664; fax (937) 656-7995; e-mail fraziewg@picard.ml.wpafb.af.mil.
Direct questions about this or any other JOM page to jom@tms.org.
| Search | TMS Document Center | Subscriptions | Other Hypertext Articles | JOM | TMS OnLine |
|---|