
An Article from the January 2002 JOM-e: A Web-Only Supplement to JOM
 |
TMS
ONLINE | TMS
PUBLICATIONS | SITE
MAP An Article from the January 2002 JOM-e: A Web-Only Supplement to JOM |
|
|
|
|
The
authors of this article are with the Centre for Numerical Modeling
and Process Analysis at the
University of Greenwich
|
Exploring traditional, innovative, and revolutionary issues in the minerals,
metals, and materials fields.
|
| OUR LATEST ISSUE |
|
|
OTHER ARTICLES IN THE SERIES |
|---|
|
|
|
Solidification and melting processes involve interactions among a range of continuum physical phenomena. The computational modeling of such processes is a significant challenge, but as the metals industry demands ever-higher quality levels, it is one that must be addressed. When considering conventional approaches, a variety of numerical tools are encountered:
Many of the problems of interest would effectively involve fluid flow, heat transfer, phase change, non-linear solid mechanics and electro-magnetics. The computational modeling of such phenomena and their interactions is complex because of the challenges associated with the heterogeneous use of different solvers in different parts of the solution domain, different mesh requirements, and, consequently, mapping problems.
This article describes two approaches to what may be called multiphysics modeling of solidification/melting processes. Two classes of problems are considered, involving
In both shape- and continuous-casting processes, a mold is filled with liquid metal that begins to cool, solidify, and to generate stress as it does so.1 The problem, especially in shape casting, is that as the metal cools and solidifies, it shrinks from the mold, which affects the cooling rate of the cast. In an attempt to model such behavior, the authors and their collaborators have developed a series of numerical algorithms and procedures, based upon FV methods, but using unstructured meshes (FV-UM) and software technologies to model all the above phenomena and their interactions.2-6 The code arising from this work, PHYSICA,7 has been employed in the analysis of a range of casting problems.
|
|
|
|
||
 |
 |
|||
|
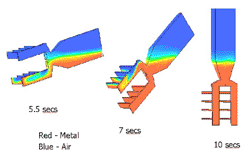
Figure 1. The photograph shows the "tree" casting experiment performed at NGL. The mold is rotated mechanically during the filling stage in the so-called Durville process. The model represents the casting and mold separately in order to compute thermal and stress interactions correctly. |
Animation 1. Filling of a complex casting by rotation with the Durville process. Simulated using the SEA algorithm in PHYSICA. |
Figure 2. The predicted and experimental miss-run of the thinnest "branch". |
||
|
|
|
|
One example of shape casting is shown in Figure
1. In the Durville casting process,1
a vessel of hot metal is slowly poured into a mold by rotation. The controlled
filling rate leads to a consistent quality in the cast component. In this
example, the cast shape is a simple tree-like geometry, designed to show a
range of defects during the casting process. The simulation involves the simultaneous
solution of free-surface turbulent flow, heat transfer, solidification phase
change, and non-linear solid mechanics.
|
|
|
|
 |
||
|
Animation 2. The development of thermal stress during cooling and cast distortion (magnified for viewing). |
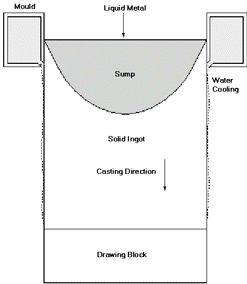
Figure 3. A schematic of the DC casting process. |
|
|
|
|
A detailed description of this simulation appears in Reference
8. A mesh of some 58K nodes and 75K elements was used requiring ~400 time
steps.
Animation 1 shows the simulation
of the mold-filling process. Here, free-surface flow, heat transfer, and solidification
phase change are all active and so modeled. The smallest leaves at the bottom
of the tree are the thinnest and are subject to miss-runs, a result of the liquid
metal solidifying before it completely fills the mold space. The simulation
can predict this highly complex behavior reasonably well, as shown in Figure
2 . The dynamic deformation behavior of the metal component is shown in
Animation 2, which demonstrates
how both the thermal stress and deformation develop during solidification.
This procedure has also been applied to the analysis of a range of other casting
processes, including direct chill (DC) casting of aluminum. In DC casting, a
block of metal is grown from a mold supported by a moving bottom block, while
liquid metal is continually poured into the sump. The schematic of the process
is shown in Figure 3; the process is
modeled as a full three-dimensional (3-D) geometry. Figure
4 shows a plot of the liquid fraction distribution indicating 3-D effects.
Figure 5 shows the thermal distribution,
liquid-metal velocity field, and effective stress contours of solidified metal,
all in a cross-section. Animation 3
shows the dynamic growth of the ingot and the development of the velocity field
of the liquid metal.
|
|
|
|
||
|
Animation 3. Direct-Chill casting of an aluminum ingot. |
Animation 4. The magnetic levitation melting of a metal droplet under gravity. |
Animation 5. The cold-crucible melting process for reactive metals. |
||
|
|
|
|
When casting reactive alloys, such as titanium aluminides, it is desirable
to minimize contact with surrounding refractory walls during the melting and
subsequent casting. In cold-crucible processes, those results are achieved
with a magnetic field that provides the energy to reheat and melt the charge,
and also acts as a force at the surface of the charge to contain the metal
as it melts, thus minimizing wall contact.
This process is very challenging to model and involves free-surface turbulent
flow with a substantial deformation of the free-surface shape; heat transfer
and melting/solidification phase change (i.e. two moving boundaries); and
magnetic-field generation with a significant boundary-layer effect that must
be resolved accurately to capture the interactions among all the phenomena.
To capture the magnetic-field boundary layer, a deforming mesh was used to capture the free-surface deformation of the metal as it melted. Originally, the authors tried to develop a computational model of this process based upon the FV-UM methods highlighted previously. However, in tracking the deforming liquid-metal free surface during melting, obtaining a numerically stable procedure appeared to be impossible. The procedure converged, after a fashion, but the free surface seemed to have spurious oscillatory modes. An alternative numerical procedure to solve the equations was then developed and implemented, based upon a spectral collocation method to provide higher-order accuracy. The developed procedure is currently axi-symmetric, and defines the free surface through a deformation of the mesh containing the initial metal block. After considerable effort, very reliable numerical performance was achieved.9-11 It has been applied successfully to various magnetically controlled processes, including the cold crucible, of course, but also the semi-levitation and full-levitation melting techniques. Starting with the latter, Animation 4 depicts the melt and suspension of a small liquid aluminum droplet, under electromagnetic and gravitational forces. The resulting complex droplet profile shapes are due to vigorous internal motion within the droplet. They reproduce the experimental observations recorded as photographic evidence by Okress.12 An example of the cold-crucible process, with dimensions drawn from the experimental equipment at the University of Birmingham (United Kingdom), is shown in Animation 5. In this animation, a cylindrical metal charge is melted in a Consarc-supplied cold-crucible furnace. Large surface envelope excursions occur at the beginning of the process, when a small volume of liquid is subjected to the full electromagnetic Lorentz force. When the ingot has melted, a more regular oscillatory behavior persists-both primary and secondary oscillations are visible, which are well-controlled numerically by the spectral-solution procedure. The temperature contours reveal that heat losses are mainly due to contact with the water-cooled base of the crucible, but also due to intermittent side-wall contact. Interestingly, on re-visiting the FV-UM solution procedure and with hindsight, it became clear that this method also showed the same type of surface oscillatory behavior; this encouraged the authors to refocus efforts on this route to achieve genuinely 3-D calculations, which are now underway.13
1. J. Campbell,
Castings (London, U.K.:Butterworth-Heinemann,
1991).
2. N. Croft, K. Pericleous,
and M. Cross, Numerical Methods in Laminar and Turbulent Fluid Flow,
Vol. 9, ed. C. Taylor and P. Durbetki (Swansea, U.K.: Pineridge Press, 1995),
pp. 1269-1280.
3. C. Bailey and M. Cross, "A
Finite Volume Procedure to Solve Elastic Solid Mechanics Problems in Three Dimensions
on an Unstructured Mesh," Int.
J. Num. Meths. in Engrg., 38 (1995), pp. 1757-1776.
4. G. Taylor, C. Bailey, and
M. Cross, "Solution of Elasto/Visco Plastic Equations: A Finite Volume
Approach," Appl. Math. Modeling, 19 (1995), pp. 746-760.
5. G. Moran et al., "Three
Dimensional Free Surface Modeling in an Unstructured Mesh Environment for Metal
Processing Applications," Appl. Math. Modeling, 22 (1998), pp. 895-906.
6. K. Pericleous et al., "Mathematical
Modeling of Solidification of Liquid Tin with Electromagnetic Stirring,"
J. Magetohydrodynamics, 32 (1996), pp. 472-478.
7. PHYSICA, see www.multi-physics.com.
8. S. Bounds et al., "A
Computational Model for Defect Prediction in Shape Castings Based on the Interaction
of Free Surface Flow, Heat Transfer and Solidification Phenomena," Metall.
Mater. Trans., 31B (2000), pp. 515-527.
9. V. Bojarevics and K. Pericleous,
"Magnetic Levitation Fluid Dynamics," J. Magnetohydrodynamics,
37 (2001), pp. 93-102.
10. K.A. Pericleous, "Computing
the Dynamic Interaction of Magnetic Fields and Turbulent Conducting Fluids in
Metals Processing," Computational
Modeling of Materials, Minerals and Metals Processing, ed. M. Cross,
J.W. Evans, and C. Bailey (Warrendale, PA: TMS,
2001), pp. 5-22.
11. V. Bojarevics, K. Pericleous,
and M. Cross, "Modeling the Dynamics of Magnetic Semi-Levitation Melting,"
Metall. Materials Trans.
B, 31B (2000), pp. 179-189.
12. E. Okress et al., J.
Appl. Phys., 23 (1952), pp. 545-552.
13. G. Djambazov, K. Pericleous,
and V. Bojarevics, "Free Surface and Mesh Control for the FV Simulation
of Semi-Levitation Melting," 8th ACME Conf. Proc., ed. M. Cross
(London, U.K.:Greenwich University
Press, 2000), pp. 4-45.
For more information, contact M. Cross, University of Greenwich, Centre for Numerical Modeling and Process Analysis, London, U.K.; +44-208-331-8702; e-mail m.cross@gre.ac.uk
Direct questions about this or any other JOM page to jom@tms.org.
| If you would like to comment on the January 2002 issue of JOM, simply complete the JOM on-line critique form | |||||
|---|---|---|---|---|---|
| Search | TMS Document Center | Subscriptions | Other Hypertext Articles | JOM | TMS OnLine |