 LATEST ISSUE |
||||
TMS QUICK LINKS: |
• TECHNICAL QUESTIONS • NEWS ROOM • ABOUT TMS • SITE MAP • CONTACT US |
JOM QUICK LINKS: |
• COVER GALLERY • CLASSIFIED ADS • SUBJECT INDEXES • AUTHORS KIT • ADVERTISE |
|
| Research Summary: Refractory Metals and Alloys | VOLUME 63, NO. 12 pp. 27-31 |
for Extreme Condition Applications
B.E. Schuster, J.P. Ligda, Z.L. Pan, and Q. Wei
Questions? Contact jom@tms.org. |
|
For the last decade, there has been research aimed at engineering plastic instability into the deformation behavior of body centered cubic (b.c.c.) metals. At dynamic strain rates, the adiabatic shear band deformation mode has been shown to improve the performance of kinetic energy penetrator materials. However, for some b.c.c. metals the transition to localized plastic deformation dominates at all strain rates. This limits the traditional engineering properties (e.g., ductility and toughness) and feasibility of incorporation into a long rod penetrator system. Recently, we demonstrated that nanocrystalline tantalum shows significant promise as it deforms via adiabatic shear bands in dynamic compression but shows significant tensile elongation in quasi-static deformation.
Extreme service conditions have
posed great challenges for the design
and manufacturing of new materials.
Examples of such conditions include
nuclear radiation, high temperatures,
environmentally hostile conditions,
and high strain rate impact. Kinetic
energy (KE) penetrators truly push
materials to the extreme. Exceptional
engineering properties (e.g., yield
strength, ductility and toughness) are
required to survive launch and flight.
During penetration into a thick armor
plate, penetrator materials that deform
by adiabatic shear band (ASB) formation
show superior performance.1–2
UFG materials are defined here as having characteristic grain sizes from 100 to 500 nm, while NC materials have grain sizes smaller than 100 nm. Wright's model for the susceptibility of viscoplastic materials to ASB formation15 has been used to guide in the materials design and processing. Details of the model and the applicability to UFG and NC b.c.c. metals will be discussed in greater detail later. In this research summary, we will focus on UFG and NC tantalum (Ta) processed by high pressure torsion (HPT). The density of Ta is generally considered too low for incorporation into real penetrator systems, though it is a model material for study as it is generally considered to be more ductile than tungsten (W). We will present our approach to systematically examine the effect of grain size on the mechanical properties and deformation modes of b.c.c. metals across a range of stress states and applied strain rates. We will show that NC Ta can be engineered to retain the ability to plastically deform under quasi-static tension and to strain localize during dynamic compression. KINETIC ENERGY PENETRATOR MATERIALS In large caliber applications, KE rounds consist of high aspect ratio long rod penetrators of either depleted uranium (DU) alloys or tungsten heavy alloys (WHAs). Launch accelerations are transferred between the grooved interface of the sabot and the mating surface on the penetrator. Muzzle velocities often approach 1.7 km/s; the associated accelerations and sabot discard require exceptional engineering properties (e.g., yield strength, ductility and toughness).
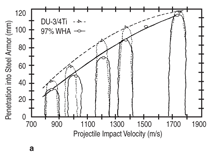
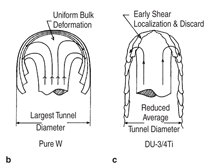
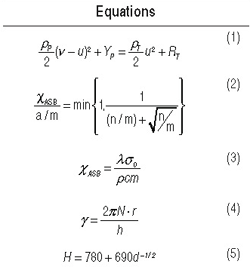
The Alekseevski–Tate equation (Equation 1) would predict very similar performance for DU and WHA, given the similarities in density and mechanical properties. However, DU alloys are well-known to have superior penetration performance to WHAs.1,2 One method to experimentally quantify the performance of KE penetrators is to measure their penetration into thick or effectively-infinite targets. Figure 1a (reproduced from Magness1) shows a comparison of the depth of penetration and traces of actual penetration tunnels from DU alloy and 97 wt.% WHA rods fired into a thick mild steel target. The penetrators were equal in density (18.6 g/cc), mass (65 g) and geometry (length to diameter ratio equal to 10). Magness reported the volume displaced for a given impact energy is nearly identical for equal density DU and WHA penetrators. WHAs show stable deformation and flow behavior during ballistic impact while DU penetrators deform via ASBs. This translates into narrower and deeper penetration channels for DU. Schematics of this deformation process for non-shearing conventional tungsten alloys and DU alloys are shown in Figure 1b,c, respectively (similarly reproduced from Magness1). The basic concepts of ASBs have been discussed in greater detail in a number of references.15,18 In the ballistic impact of DU alloys, thermal softening from plastic work quickly overwhelms the stabilizing influences of strain hardening and strain rate sensitivity.1,2 DU alloys have a lower specific heat and melting temperature than WHAs, which adds to the relative tendency for ASB formation. WHAs however, typically show higher strain rate sensitivities than DU alloys. This stabilizing influence tends to suppress strain localizations. For an in-depth discussion of the comparison of DU and WHA, readers should refer to the original works by Magness. MOTIVATION FOR UFG AND NC METALS UFG and NC metals have been considered for KE penetrator applications. Because of the Hall19–Petch20 effect, these materials typically show increased yield strengths relative to their coarse grained (CG) counterparts; improvements in performance for these high strength materials are implied by Equation 1. Perhaps more importantly, UFG and NC b.c.c. metals can show localized plastic deformation during dynamic compression.4,7–9,12 The most significant accomplishment to date has been demonstration of this deformation mode in UFG and NC tungsten (W).9,12 There is limited evidence that a similar transition in deformation mode resulted in improved penetration performance in a relatively low-density nanocrystalline tungsten composite alloy.21
Wright's model for the susceptibility
of visco-plastic materials to ASB
formation can be used to describe the
motivation for fine grained metals.
Wright15 derived Equation 2 for
Grain size reductions in b.c.c. metals
typically result in a significant increase
in their susceptibility to ASB formation
through associated changes in the
strength, strain hardening behavior
and SRS. NC metals are considerably
stronger than their CG counterparts.
UFG and NC b.c.c. metals show little
strain hardening and are often assumed
to behave as a perfectly plastic material
(no strain hardening).8,10–12,14 The
SRS of b.c.c. metals typically decreases
with the characteristic grain size,7
though Ta does not appear to follow
this dependence in the lower bound
of the nanocrystalline regime.14 For
perfectly plastic materials, the susceptibility
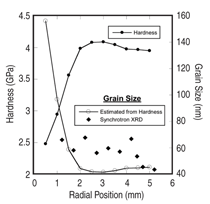
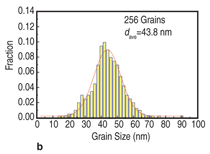
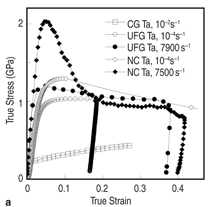
reduces to Equation 3 where In some b.c.c. systems, localized plastic deformation has been found to dominate the response under quasistatic and dynamic deformation.4,7 There is concern that localized plastic deformation at low to moderate strain rates will inherently limit the engineering properties of these materials and their eventual applicability in KE penetrator systems. As mentioned earlier, the launch forces experienced by KE penetrators require exceptional engineering properties at low to moderate strain rates. Other than a few isolated studies23 the tensile properties of UFG and NC b.c.c. metals are largely unknown. The tensile properties of these materials will be studied along with their propensity to deform via ASBs at higher strain rates. STRATEGY AND METHODOLOGY In this research summary, we will focus the discussion on tantalum. Similar studies on W and other b.c.c. metals from groups V and VI on the Periodic Table are underway. Severe plastic deformation (SPD) was used to refine the grain size of CG Ta into the UFG and NC regime. Specifically, commercial purity tantalum disks were processed by high pressure torsion (HPT) by Valiev. 24 In HPT processing, samples are confined at high pressures between two opposing Bridgeman anvils and the disks are deformed in torsion. The local shear strains vary as a function of radial position (distance from the center of the disk, r), and the number of turns, N, as shown in Equation 4.25 The material presented here was confined at a pressure of ~5 GPa, and was deformed at room temperature in torsion to maximum strains approaching 9,000% (N=5). The site-specific indentation behavior was examined using microhardness testing and nanoindentation. Microstructures were characterized in a transmission electron microscope (TEM)14 and with synchrotron based x-ray diffraction.26 The dynamic compressive response was investigated using a desktop Kolsky bar apparatus.27 Readers should refer to Wei and coworkers for a more detailed discussion on the dynamic compression tests.5,14 The HPT processed samples yield very small volumes of material. As mentioned previously the total volume is a thin disk that is roughly 10 mm in diameter. Even the largest specimens are too small to test in a conventional Kolsky bar, and are difficult to fabricate and handle for conventional quasistatic uniaxial testing. Instead, focused ion beam (FIB) based micromechanical testing methods were employed to investigate the quasi-static properties. Microcompression specimens were fabricated and tested using the methodologies discussed in detail by Uchic and Dimiduk.28 Micro- and nano-compression experiments have been used extensively in the literature to examine the size-dependent mechanical properties of materials.29–32 However, here we have used this technique to probe the site-specific "bulk" properties of UFG and NC Ta. Assuming a grain size of 50 nm, a pillar with a 5 mm diameter would possess nearly ~1.6 million grains. For comparison, a CG bulk sample that is several millimeters in diameter would have a similar number of crystallites. One could argue these measurements of micro-specimens could represent bulk response, though this is not considered in depth in this summary. "Dog-bone" microtension specimens are fabricated using micro-electro discharge machining followed by final machining with the FIB. In-situ scanning electron microscope (SEM) tension tests were performed in a custom test stage.33 The stage is similar in principle to another presented elsewhere. 36,35 Tensile specimens were positioned in a grip (milled from a high aspect ratio tungsten needle) using a 3-axis piezoelectric stage. Loads were applied using a linear actuator with a reported resolution of ~1 nm and were measured using a data acquisition program from a strain gage based S-beam load cell (capacity of 100 g and resolution of ~0.01 g). Strains were calculated from successive SEM micrographs taken during testing using the open source digital image correlation script developed by Eberl and coworkers.36 Given the variation in strain as a function of radial position (Equation 4), it follows that the microstructures and extent of grain refinement vary as a function of position on the bulk HPT specimens. Microhardness measurements illustrate the variation in strength as a function of radial position as shown in Figure 2. The hardness quickly climbs from ~2.5 GPa at r~0.5 mm to over 4 GPa at r~2.5 mm. The hardness remains comparatively constant for r > 2.5 mm. The grain size, d (in nanometers), for each radial position was estimated from the hardness, H (in GPa), using the Hall–Petch relation for Ta37 given in Equation 5. Grain sizes were also estimated from synchrotron x-ray peak broadening.26 Both estimates for grain size as a function of radial position are plotted in Figure 2. Grain size estimates from x-ray peak broadening and hardness are comparable. The estimates indicate the grains are UFG near the center and the threshold for transition into the truly NC occurs around r~1 mm. Figure 3 shows a TEM micrograph and the associated grain size distribution for a specimen cut near r~2 mm which confirms the characteristic NC grain size. Mainly equiaxed grains with an average grain size of 43 nm were found.14 Figure 4 shows the compressive response of pure Ta over a wide range of grain sizes and applied strain rates. CG Ta showed a comparatively low compressive yield strength and showed significant strain hardening.5 UFG compression samples were cut near the center of the HPT disk and are significantly stronger than CG Ta; yield stresses exceeding 1 GPa were typical.14,26 This and other UFG samples deformed in microcompression showed little to no strain hardening though plastic buckling may complicate analysis of the true strain hardening response.14 The UFG specimen tested in dynamic compression showed some strain softening. UFG specimens showed at most evidence of fairly diffuse strain localization. In contrast, localized plastic deformation was found in quasi-static and dynamic compression of NC Ta as shown in Figure 4b and c. In microcompression tests, shear bands were found for specimens near the extreme edge of the specimens (r>5 mm).26 It is unlikely that the shear bands were adiabatic in nature; however there is a clear change in deformation mode. Adiabatic shear bands were found in dynamic compression of the NC Ta.14 The NC sample shown in Figure 4a had a yield strength exceeding 2 GPa followed by a sharp stress collapse after yielding. The yield strengths of dynamically deformed NC Ta samples were significantly higher than the quasi-static compression specimens though this is not necessarily due to strain rate sensitivity. The UFG and NC Ta show little strain hardening and deform in a manner that is effectively elastic-perfectly plastic. The microcompression specimens had an aspect ratio (ratio to length to diameter) of ~2 and were therefore more prone to structural instability which can affect the measured response.
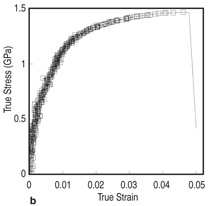
Investigations of the tensile properties
of UFG and NC Ta are still in the
early stages,26 but a demonstration of
the approach is presented in Figure 5.
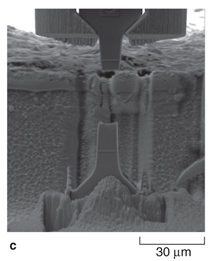
Figure 5a shows an SEM micrograph
of a typical microtension specimen
loaded in the grip. The stress-strain response
for a tension sample cut at position
r~3.9 mm is presented in Figure
5b. Figure 2 would suggest the grain
size of this specimen is roughly 40 to
60 nm. The minimum cross-section of
the sample was roughly 9 The mechanical properties of this NC Ta are an encouraging sign that UFG and NC b.c.c. metals may one day be viable alternatives for KE applications; NC Ta shows some tensile elongation at quasi-static strain rates and ASB formation during dynamic compression. Microcompression experiments indicate a critical grain size for transition in quasi-static deformation mode may occur around ~50 nm.26 In practice, transition to this deformation mode in penetrator materials should be largely avoided in order to retain materials that can be launched in actual long rod KE penetrators. While some of the basic concepts of shear band formation in UFG and NC b.c.c. metals have been examined in uniaxial mechanical testing, there are no known accompanying ballistic demonstrations of this concept. Top-down and bottom-up processing routes will need to be developed to manufacture sizable samples of fully dense materials for ballistic tests. For example, HPT processing commonly yields a thin sample that is roughly ~10 to 12 mm in diameter. By comparison, the 65 g sub-scale penetrator rods fired by Magness1 were nearly ~8 mm in diameter and ~80 mm long. Equal channel angular extrusion has been investigated as an alternative processing route, though this process alone has not been suffi - cient to induce ASBs in Ta5 or W.9,10 However, the collection of work to date and the exceptional combination of properties of NC Ta show that this class of materials may one day offer an alternative to DU alloys. The mechanical properties of UFG and NC Ta were investigated by using site-specifi c microstructural analysis and mechanical testing of samples processed by HPT. A single HPT processed sample shows gradient in microstructures and mechanical properties, with grain sizes ranging from the truly nanocrystalline to several hundred nanometers in diameter. Consistent with Wright?s model for susceptibility to ASB formation, NC Ta shows a transition in deformation mode owing to its enhanced strength and reduced strain hardening relative to CG Ta. An early demonstration shows that NC Ta retains the ability to plastically deform in quasi-static tension testing. This work indicates that UFG and NC metals may have promise in KE penetrator applications. The authors are grateful to L.S. Magness, W.N. Sharpe, B.G. Butler, X.L. Wu, and L.J. Kecskes; and would like to thank Professor R.Z. Valiev for providing the HPT Ta. Q. Wei would like to acknowledge the support from U.S. Army Research Laboratory under Contract No. W911QX-06-C-0124 and W911QX-08-C-0073.
1. L.S. Magness and T.G. Farrand, "Deformation Behavior
and its Relation to the Penetration Performance
of High-Density KE Penetrator Materials," Proceedings
of the Army Science Conference (Durham, NC:
Defense Technical Information Center, 1990), pp.
465-479.
B.E. Schuster is with the Weapons and Materials Research Directorate, U.S. Army Research Laboratory, Aberdeen Proving Ground, MD 21005, USA; brian.e.schuster@usarmy.mil; J.P. Ligda, Z.L. Pan, and Q. Wei are with the University of North Carolina at Charlotte, 9201 University City Blvd., Charlotte, NC 28223. |






 Alekseevski16 and Tate17 independently derived one-dimensional KE
projectile penetration models. Their
models follow a general framework
incorporating the strength of the penetrator
material, Y, and the resistance
(strength) of the target material, R. Given
penetrator density,
Alekseevski16 and Tate17 independently derived one-dimensional KE
projectile penetration models. Their
models follow a general framework
incorporating the strength of the penetrator
material, Y, and the resistance
(strength) of the target material, R. Given
penetrator density, 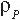 , target density,
, target density,
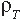 , the relation between the striking velocity,
v, and the penetration velocity,
U, is given in Equation 1. From inspection
of this model, it follows that highdensity
and high-strength materials are
desirable for this application.
, the relation between the striking velocity,
v, and the penetration velocity,
U, is given in Equation 1. From inspection
of this model, it follows that highdensity
and high-strength materials are
desirable for this application.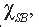 ,
called the susceptibility to ASB, where a is the non-dimensional thermal softening
parameter defined by a =
,
called the susceptibility to ASB, where a is the non-dimensional thermal softening
parameter defined by a = 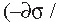
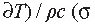 is the flow stress, T the temperature,
ρ the density, and c the specific
heat of the material), n the strain
hardening exponent, and m the strain
rate sensitivity (SRS).
is the flow stress, T the temperature,
ρ the density, and c the specific
heat of the material), n the strain
hardening exponent, and m the strain
rate sensitivity (SRS).
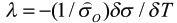 is the thermal
softening parameter evaluated under
isothermal conditions
is the thermal
softening parameter evaluated under
isothermal conditions 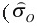 is a normalizing
stress), and σO is the yield
strength. Application of this model to
UFG and NC shows that these materials
exhibit a significant increase in susceptibility
to adiabatic shear band formation
than their CG counterparts.8,10–12,14
Recent numerical simulations on the
effects of microstructure suggest that
UFG/NC b.c.c. metals are more prone
to form ASB.22
is a normalizing
stress), and σO is the yield
strength. Application of this model to
UFG and NC shows that these materials
exhibit a significant increase in susceptibility
to adiabatic shear band formation
than their CG counterparts.8,10–12,14
Recent numerical simulations on the
effects of microstructure suggest that
UFG/NC b.c.c. metals are more prone
to form ASB.22
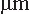 in width
and thickness and the overall length
was ~65
in width
and thickness and the overall length
was ~65