|
A multi-scale, computational design
approach for aluminum sheet alloys,
which includes key inputs from the
electronic, atomistic, microstructural,
and continuum length scales, is reviewed
within the context of room and
elevated temperature forming. Specific
examples, which are aimed at improving
aluminum sheet materials for automobile
components, include prediction
of flow curves from tensile testing,
forming limit diagrams, and component
forming.
INTRODUCTION
| HOW WOULD YOU... |
…describe the overall significance
of this paper?
This paper provides an approach to
modeling deformation in aluminum
sheet materials using input from
a variety of length scales. It
demonstrates how information
from electronic and atomistic
level calculations can be used in
calculations of engineering forming
processes.
…describe this work to a
materials science and engineering
professional with no experience in
your technical specialty?
This work provides an approach for
using a variety of microstructural
information into constitutive
equations for metalforming. It
describes the framework for linking
atomistic calculations with finite
element simulations of forming.
…describe this work to a
layperson?
This work describes an approach
whereby one can predict how
changing the composition of a metal
or its microstructure can influence the
ability to make automotive parts.
|
The range and complexity of materials
now used in metal forming processes
is continually expanding the gap
between simulation and the availability
of accurate constitutive models and
failure criteria to represent their behavior.
In the auto industry, there is a need
to utilize lightweight metals such as advanced
high strength steels, aluminum,
and magnesium to improve vehicle
fuel economy and performance. Due
to their limited formability, these materials
often require novel forming processes
which utilize load cases, temperatures,
and strain rates that are not
common in automotive manufacturing.
The constitutive equations which
govern the forming and performance
of these materials are typically developed
through extensive mechanical
testing and characterization which is
time consuming and expensive. Moreover,
material model development is
largely dependent on continuum scale
phenomena and ignores the rich multiscale
physical and chemical phenomena
that are responsible for the macroscale
plastic deformation response of a
polycrystalline metal. The substantial
complexity of these phenomena, which
occur through the evolution of microstructure and texture in response to
strain, presents formidable challenges
to theoretical model development of
plastic deformation.
General Motors Company, with
Brown University and other collaborators,
is engaged in an "Atoms to
Autos" research program to develop
computational techniques to speed
the development of lightweight sheet
materials and their deformation processes
to enable increased use of these
materials in the automotive industry.
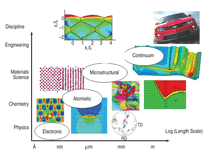
The framework that we have used is
based upon a multi-scale modeling approach,
shown schematically in Figure
1, which requires a deeper understanding
of operative metallurgical phenomena during deformation. The inference
from Figure 1 is that the process of
multi-scale modeling of material constants
requires inputs from different
length scales, the smallest of which is
the length scale over which electronic
structure is accounted for (up to ~103
atoms), and the largest being the continuum
which is the domain of engineering.
In between lie the atomistic (≤104
atoms) and microstructural (grain size)
length scales. Our multi-scale modeling
approach employs a combination
of modeling techniques including
quantum mechanical (QM) description
of electronic structure via density functional
theory (DFT), molecular dynamics
(MD), crystal mechanics/plasticity,
and continuum finite element modeling
(FEM). Details about each of these calculations
and their outputs are summarized
in Table I.

Our approach is tailored to the
unique aspects of a given material,
with the thrust being an understanding
of the key physical and chemical
mechanisms that govern plastic deformation
behavior. The desired outcome
is the ability to develop inputs to FEM
simulations through computational approaches
with the use of embedded or
informed constitutive equations and
failure criteria rather than experimental
characterization and data-fitting. This
approach can also provide input data
to higher length scale models when
experimental data is not available or is
difficult to generate and thus reduce the
number of approximations needed for
numerical simulations. The ultimate
goal of this multi-scale approach is to
develop new materials with improved
formability and end-use performance,
and to improve upon the finite element
prediction of their forming and performance
with informed constitutive equations.
In this paper, we highlight our recent
successes in multi-scale modeling of
Al-Mg alloys. These alloys have already
seen extensive use in automobiles
in the form of AA5182, AA5754,
and AA5083 and they offer an excellent
combination of formability and
strength. We have selected five different
types of calculations to demonstrate the
approach. These include predicting the
effect of solutes on yield strength, solutes
on strain rate sensitivity in tensile
behavior, hardening and microstructure
effects on forming limit diagrams, microalloying
on grain boundary sliding,
and various deformation mechanisms
active during high temperature forming.
For clarity of presentation, these
examples are discussed in two separate
sections: one applicable to room temperature
forming, such as conventional
stamping, and the second for elevated
temperature forming processes, such
as quick plastic forming (QPF). The
individual approaches and calculations
are summarized, and the opportunities
for using these calculations in material design are highlighted
ROOM-TEMPERATURE DEFORMATION
Conventional stamping at room
temperature is the primary method
for making automotive body panels,
which presents a challenge for aluminum
sheet materials due to their lower
formability compared to steel. A large
portion of our multi-scale modeling
initiative focuses on calculations to
improve the development of new aluminum
materials for room-temperature
stamping. The challenge is to develop
materials with formability comparable
to cold rolled steel, without compromising
strength or other performance
attributes such as corrosion, paintability,
etc.
The strength of Al-Mg alloys is
mainly controlled by solute strengthening.
The addition of magnesium
solute up to 5 wt.% has been shown
to increase strength without reducing
ductility.1 However, one of the key
drawbacks to many Al-Mg alloys is
that they exhibit a negative strain rate
exponent sensitivity (nSRS) or m, and
dynamic strain aging (DSA) at room
temperature. Associated with the nSRS
is reduced ductility, which compromises
formability and can produce irregularities
on the surface of formed parts
which limits their use to non-exposed surface
applications.2
Electronic Structure
Central to theoretical models of
solute strengthening and diffusion are
accurate dislocation core structures.
Since dislocation core structure cannot
be predicted by classical continuum
elasticity dislocation models, we combined
DFT3 with the Lattice Green's
function (LGF) technique4 to predict
the core structure of an aluminum
edge dislocation. The DFT formalism,
which is now one of the important
computational materials science
tools,5 provides energies, while the
LGF technique correctly couples dislocation
core structure to the long range
elastic field of the dislocation. We find
that an aluminum edge dislocation, for
example, dissociates into two Shockley
partials separated by ~10.8 Ε.6 This
very narrow core spreading presents
significant challenges to experimental investigations of dislocation structure
in aluminum.
With the DFT-predicted core structure,
we focused on solute strengthening.
We first computed solute/dislocation
interaction energies for a range of
relevant solute additions with DFT for
solutes in the immediate core (i.e. in the
stacking fault region) of an aluminum
edge dislocation (a similar procedure
applies for the screw core). We limit
our focus here to magnesium solutes.
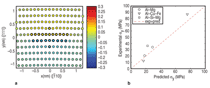
Figure 2a shows contours of U (xi, yj),
which is the solute/dislocation interaction
energy as a function of position
(xi, yj) in the DFT-predicted core. To
accomplish this, we placed solutes at
the sites denoted by darkened circles.
Favorable binding energies are denoted
by negative values (energies are in eV),
so that magnesium prefers to reside on
the tension side of the core: this is consistent
with the fact that magnesium
solute is larger than the Al.
The interaction energies were then
used in a parameter-free analytic theory
that enables prediction of 0K shear
flow stress, τy0, for binary Al-Mg alloys
as a function of temperature and strain
rate.6 The theory considers the motion
of a dislocation through a random distribution
of solutes in the host matrix.
The derivation is beyond the scope of
this article, and so we simply quote
the major results (Equation 1), where
c is solute concentration, b is Burgers
vector, 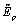 is a characteristic energy
associated with the collective solutedislocation
interaction energies in the
random alloy (directly related to the
interaction energies shown in Figure
2a), wc is a characteristic dislocation
"roughening" amplitude arising as the
dislocation meanders to search out favorable
(low energy) fluctuations in the
solute field (calculated within the theory),
and Γ is the dislocation line energy.
The finite temperature yield strength,
τy (T), at is a characteristic energy
associated with the collective solutedislocation
interaction energies in the
random alloy (directly related to the
interaction energies shown in Figure
2a), wc is a characteristic dislocation
"roughening" amplitude arising as the
dislocation meanders to search out favorable
(low energy) fluctuations in the
solute field (calculated within the theory),
and Γ is the dislocation line energy.
The finite temperature yield strength,
τy (T), at 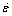 is then the stress needed
to generate a rate of thermal activation
over the energy to achieve plastic
flow at the specified strain rate. This is
given by Equation 2, where T is temperature,
and the energy barrier that the
dislocation must overcome is given in
Equation 3. Here, is then the stress needed
to generate a rate of thermal activation
over the energy to achieve plastic
flow at the specified strain rate. This is
given by Equation 2, where T is temperature,
and the energy barrier that the
dislocation must overcome is given in
Equation 3. Here, 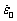 ~104–106 s–1 is a
reference strain rate. Quantitative comparisons
with experimental are shown
in Figure 2b.7,8 There are two concentrations for both Al-Mg (0.444% and
0.810%) and Al-Cu-Fe (0.090/12Χ106
and 1.65%/50Χ10–6). Al-Mg-Si-(Fe)
concentration is 0.365%/0.823%. Lower
concentrations correspond to lower
stresses. The predictions for the Al-Mg
alloys are in exceptional agreement
with the experimental values. (All
equations are presented in the table.) ~104–106 s–1 is a
reference strain rate. Quantitative comparisons
with experimental are shown
in Figure 2b.7,8 There are two concentrations for both Al-Mg (0.444% and
0.810%) and Al-Cu-Fe (0.090/12Χ106
and 1.65%/50Χ10–6). Al-Mg-Si-(Fe)
concentration is 0.365%/0.823%. Lower
concentrations correspond to lower
stresses. The predictions for the Al-Mg
alloys are in exceptional agreement
with the experimental values. (All
equations are presented in the table.)

Atomistic
Models of DSA and nSRS incorporate
a critical resolved shear stress
(or resistance to dislocation glide) of
the form Equation 4, where τ0s
is due to other strengthening mechanisms
(strain hardening, and SRS associated
with the activation of overcoming
short-range obstacles in the absence
of nSRS). The standard form for additive
strengthening (or resolved shear
stress to move a dislocation), Δτs (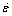 ),
applied in DSA/serrated flow studies
is Equation 5. Here, the prefactor Δτ0,
the characteristic strain rate for diffusion ),
applied in DSA/serrated flow studies
is Equation 5. Here, the prefactor Δτ0,
the characteristic strain rate for diffusion
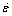 *, and (sometimes) n are treated
as fitting parameters to experimental
stress drops in serrated flow curves
from tensile tests. Subsequent predictions,
however, are often inconsistent
with experiments. For example, predicted
values of Δτ0 and *, and (sometimes) n are treated
as fitting parameters to experimental
stress drops in serrated flow curves
from tensile tests. Subsequent predictions,
however, are often inconsistent
with experiments. For example, predicted
values of Δτ0 and 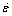 * for Al-Mg
with a bulk solute (Mg) concentration
of co = 2.5% are 500–5,000 MPa
(10–100 times too large) and ~10–11 s–1
(six orders-of-magnitude too small),
respectively.9 Moreover, solute binding
energy is predicted to be as high as
50 eV, which is enormous. To address
these problems, we derived an analytic
expression for Δτs ( * for Al-Mg
with a bulk solute (Mg) concentration
of co = 2.5% are 500–5,000 MPa
(10–100 times too large) and ~10–11 s–1
(six orders-of-magnitude too small),
respectively.9 Moreover, solute binding
energy is predicted to be as high as
50 eV, which is enormous. To address
these problems, we derived an analytic
expression for Δτs (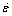 ) that justifies the
widely used phenomenological form
and which leads to predictions of important
quantities that are in agreement
with experimental values.9 We identified
a new mechanism for DSA called
"cross core" diffusion and applied it
to strengthening due to magnesium
diffusion in Al-Mg alloys. Here, only
magnesium solute immediately on the
compression side of the slip plane diffuses,
in one step of atomic motion, to
the immediate tension side of the slip
plane. This process is highly localized in the dislocation core, and terminates
when the supply of solutes on the immediate
compression side of the core
is exhausted, leading to a finite (and
modest) strengthening consistent with
experimental values. Most importantly,
the rate of diffusion in the core is a
factor of 106 times faster than normal
magnesium diffusion in bulk aluminum.
The fast diffusion is due to the
highly distorted environment in the
dislocation core region. Since the process
involves diffusion, it is explicitly
time-dependentthe longer a dislocation
remains at its pinned location, the
more solutes diffuse, and the stronger
the material becomes. Thus, the material
becomes stronger at lower strain
rates (slower escape of dislocations
from their pinned positions), which
corresponds to nSRS. ) that justifies the
widely used phenomenological form
and which leads to predictions of important
quantities that are in agreement
with experimental values.9 We identified
a new mechanism for DSA called
"cross core" diffusion and applied it
to strengthening due to magnesium
diffusion in Al-Mg alloys. Here, only
magnesium solute immediately on the
compression side of the slip plane diffuses,
in one step of atomic motion, to
the immediate tension side of the slip
plane. This process is highly localized in the dislocation core, and terminates
when the supply of solutes on the immediate
compression side of the core
is exhausted, leading to a finite (and
modest) strengthening consistent with
experimental values. Most importantly,
the rate of diffusion in the core is a
factor of 106 times faster than normal
magnesium diffusion in bulk aluminum.
The fast diffusion is due to the
highly distorted environment in the
dislocation core region. Since the process
involves diffusion, it is explicitly
time-dependentthe longer a dislocation
remains at its pinned location, the
more solutes diffuse, and the stronger
the material becomes. Thus, the material
becomes stronger at lower strain
rates (slower escape of dislocations
from their pinned positions), which
corresponds to nSRS.
From our model, we are able to
predict expressions for Δτ0, 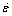 * and
n, thereby eliminating the need for
data fitting (Equations 6–9), where, * and
n, thereby eliminating the need for
data fitting (Equations 6–9), where, 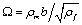 ρm and ρf are mobile
and forest dislocation densities, β = 1/
kT (k = Boltzmann's constant), ρm and ρf are mobile
and forest dislocation densities, β = 1/
kT (k = Boltzmann's constant), 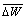 is
the average enthalpy difference across
the core, α is a constant, ΔHC is the activation
enthalpy for bulk diffusion of
magnesium in aluminum, and v0
is the
attempt frequency (or frequency that
an magnesium solute will try to escape
its current position so as to move to a
different position due to thermal fluctuations).
For Al-Mg with c0 = 2.5%Mg
and literature material properties, the
model predicts Δτ0 = 14.5 MPa and is
the average enthalpy difference across
the core, α is a constant, ΔHC is the activation
enthalpy for bulk diffusion of
magnesium in aluminum, and v0
is the
attempt frequency (or frequency that
an magnesium solute will try to escape
its current position so as to move to a
different position due to thermal fluctuations).
For Al-Mg with c0 = 2.5%Mg
and literature material properties, the
model predicts Δτ0 = 14.5 MPa and 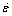 *
= 4.5 Χ 10–5 s–1 which agree well with
experiments.10 Moreover, measureable
DSA effects are accurately predicted
over a range of strain rates (10–6 – 10–1
s–1) and temperatures (233–353 K) that
are consistent with experimental studies.
Calculation of the strain rate sensitivity,
m( *
= 4.5 Χ 10–5 s–1 which agree well with
experiments.10 Moreover, measureable
DSA effects are accurately predicted
over a range of strain rates (10–6 – 10–1
s–1) and temperatures (233–353 K) that
are consistent with experimental studies.
Calculation of the strain rate sensitivity,
m(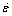 ) = d(ln τ) / d (ln ) = d(ln τ) / d (ln 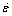 ), using
Equations 4, 6–9 (for τ0s = 60 MPa)
also resulted in good agreement with
experiments.10 ), using
Equations 4, 6–9 (for τ0s = 60 MPa)
also resulted in good agreement with
experiments.10
The cross-core diffusion mechanism
was validated using our multi-scale
modeling approach. This involved two
atomistic techniques: molecular statics
(which uses semi-empirical potentials
rather than quantum mechanics) to
predict magnesium energies in the aluminum
core, and kinetic Monte Carlo
(kMC) to validate the effect of magnesium
cross core diffusion. In kMC,
magnesium atoms are moved toward
their equilibrium (i.e., energetically
preferred) sites at a rate corresponding
to their local diffusion rate at a specified
temperature. Each atom movement
is based upon a computed probability
for that movement.
We have developed a full rate theory
for plastic flow in the presence of
DSA incorporating the theory outlined
above. We find that the cross-core
process, which occurs on all dislocations,
both mobiles and forests, has
an important influence on the forest
strengthening contribution to the alloy
stress-strain response. The full rate theory,
with inclusion of forest hardening
and DSA effects on the forest hardening,
is described in Reference 11. This
development enables us to implement
the atomistically informed constitutive
law into a robust continuum-level
model such as the commercial code
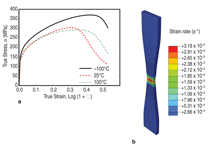
ABAQUS.12 An example of the predictive
capability of this overall model
is shown in Figure 3. The predicted
stress-strain curves for a standard tensile
specimen of AA5083 shown as a
function of temperature. The model demonstrates the reduced ductility
at 25°C where this material exhibits
nSRS.
Microstructural Effects
In the atomically informed analytical
model approach discussed above, we
have considered the solute dislocation
interaction and the dynamics of mobile
and forest dislocation interactions with
solutes, neglecting the dislocation and
dislocation interactions as they occur
during hardening. In general, the accuracy
of any constitutive model depends
on the theory that it is based on. A
polycrystal model can be derived from
single crystal deformation models to
include anisotropic properties of single
crystals, slip and/or twinning mechanisms,
lattice rotation, and microstructural
attributes such as grain size, grain
shape, texture etc. Currently, finite element
simulation codes rely on single
crystal constitutive laws calibrated
against polycrystalline data to reflect
the complexity in the microstructure,
hardening mechanisms etc., through
approximations and fitting parameters.
The challenge becomes the ability to
establish a realistic, physically-based
relation between the single crystal and
polycrystalline models which therefore
creates improved constitutive models.
Many different approaches have
been published in the literature to account
for dislocation-dislocation interactions
that include self and latent
hardening effects in single crystals and
polycrystals. Examination of the models
and experimental data shows that
serious deficiencies remain in accounting
for hardening behavior even in single
crystal aluminum. One such area is
the way latent hardening is accounted
for in constitutive models.
Many different amounts and rates of hardening of different
slip systems have not been accurately
incorporated to predict the
crossover in hardening curves along
different crystallographic directions in
face-centered cubic (f.c.c.) crystals for
example.13 The measured latent hardening
coefficients (LHC) in aluminum
have values between 1 and 4, contrary
to the typical assumptions available in
the literature (0~1.4).14–16 This becomes
important in simulating lattice rotation
and texture evolution from a "finite
element per grain" approach,17 which incorporates
single crystal constitutive
law and experimentally measured
grain morphology and grain orientation
information into polycrystal plasticity
simulation to assess formability and
forming limit curves. If single crystal
constitutive equations do not include
hardening in an accurate manner, the
texture evolution and grain rotation,
both of which are important in forming
operations involving complex strain
paths, are either underpredicted or
overpredicted by polycrystal plasticity
models.
Lacking the development of a fully
atomistically informed model, we have
taken the approach to deal with the inadequacies
at their level and creating
the formalism in a way that can include
any advanced hardening law into this
model when it is developed and validated.
One example of this approach
is the way we have addressed the deficiency
in the implementation of latent
hardening in a fundamental manner.
Our approach in this case involves four
main steps. First, effects such as latent
hardening or thermally activated/athermal
hardening are modeled and tested
for self consistency in controlled single
crystal samples. Instead of fixed values
for latent hardening coefficients,
an evolution law to correlate the latent
hardening coefficient 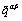 see Equation 10) and the slip system strengths is used.18 see Equation 10) and the slip system strengths is used.18
Secondly, the predictions of these
models are validated against independent
experiments. As shown in Figure
4, this law is not only capable of
predicting the overshoot tendency in
lattice rotation for FCC materials, but
also reproduces the experimental values
of lattice rotation in an aluminum
single crystal where such data is available.
Thirdly, these laws are implemented
into FEM codes through user
material subroutines for bulk simulations
via an embedded representative
volume element (RVE) approach
whose predictions can be compared
with forming data from real materials.
Such models successfully predict
localization in polycrystals due to
inhomogeneous deformation accompanying
texture evolution. Lastly, by
taking the experimental electron backscatter
diffraction data as the input for
a polycrystalline AA5754 sample, and incorporating any hardening law (such
as the ones described above or the ones
available in the literature), the forming
limit diagram (FLD) for AA5754
sheets has been successfully computed
and compared. The superior agreement
between the computed FLD following
this approach and experimental data
shown in Figure 4b highlights how the
microstructure-based model with physical
mechanisms incorporated in the
constitutive relations can discern the
relative advantages and disadvantages
of different constitutive approaches in
modeling formability. In Figure 4b,
(reproduced from Reference 20) the inadequacy
of the Bassani–Wu law over
the Saimoto–van Houte hardening law
to predict FLD in AA5754 alloys is obvious
although for simple strain path
simulations such as tensile loading,
such differences are not apparent. Evolution
of inhomogeneous deformation
at large strains is inherently included in
such an approach for the simulation of
FLDs, improving upon approximations
such as the M-K analysis used in the
continuum level models. Zhang et al.21
have shown that in single crystal aluminum,
the value of strain to localization
is highly sensitive to latent hardening
behavior, underscoring the need for
accurate hardening laws to be used in
any FLD simulation.
Material Design Opportunities
and Challenges
The results above show that it is
possible to use microstructure-based
models informed by constitutive laws
derived using physics of solute-dislocation
and dislocation-dislocation interactions
to compute forming behavior.
This approach, through "reverse
engineering," also enables designing
materials for improved formability by
manipulating alloy chemistry at the
atomic level and microstructure at the
design at grain level.
If the strength of Al-Mg alloys can
be improved by either optimizing the
magnesium content and/or the addition
of other solutes, then the need for agehardening
treatments could be reduced
or even eliminated, stress corrosion
cracking concerns could be greatly
minimized, and improved weldability
could be realized. We have investigated
other solutes in aluminum alloys besides magnesium, namely silicon, and
copper solutes among others to explore
this aspect. The use of DFT allows, in
principle, for the introduction of any
element from the periodic table. Compared
to magnesium, silicon, and copper
atoms are smaller than aluminum
atoms and hence these solutes will prefer
to migrate to sites on the compression
side of the dislocation core. The
yield stress values in Figure 2b show
that the predicted values for Al-Si and
Al-Cu deviate from experiment. The
difference between theory and experiment
for these alloys is believed to be
due to the presence of ppm levels of
iron in the nominally binary experimental
alloys.22
Other design variables such as solute
concentration, forming temperature,
and starting microstructure can
similarly be explored and optimized
using the above approach as these are
inputs to the model and their influence
on specific parameters in the constitutive
relations are exactly known, unlike
in phenomenological models where
any parameter from the curve fitting
procedure cannot be directly correlated
with any microstructural or physical
attribute of the material. The future
for improving materials and processes
rests on creating a polycrystal model
informed by theory at lower length
scales and accurately accounting for
the mechanisms and microstructural
details.
ELEVATED TEMPERATURE FORMING
The limited formability of aluminum
has led to development of alternative
forming processes to enable complex
parts to be manufactured.23 Many of
these processes, such as superplastic
forming (SPF) and quick plastic forming
(QPF), use elevated temperatures
to improve formability. These processes
require aluminum materials with
fine (<10 μm) grain sizes to enable
grain boundary sliding and give a positive
strain rate sensitivity. As a result,
these materials are often more expensive
than commercial-grade materials.
The focus of the present multi-scale
research is to develop materials which
can give improved elevated temperature
performance (for example, biaxial
dome height) and that can be processed in a cost effective manner.
Modeling of Grain Boundary
Sliding
Grain boundary sliding (GBS) is
a dominant deformation mechanism
during elevated temperature forming
of aluminum. The grain size, composition,
and grain boundary orientation
distribution play particularly important
roles in determining flow stress
and strain rate sensitivity. GBS of two
grains under an external shear stress
can be modeled by non-equilibrium
molecular-dynamics (NEMD) (see
Figure 5a).24 For pure aluminum, we
found GBS velocity is linear function
of the applied shear stress, as shown in
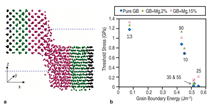
Equation 11, where &sigmaa;C is the threshold
stress, below which no sliding occurs
and η is the grain boundary viscosity.
The threshold stress decreases with increasing
grain boundary energy for various
grain boundaries we tested (Figure
5b). When the applied shear stress is
too high, sliding accelerates with a premelting
zone at the grain boundary.24
The influences of vacancies25 and solute
atoms on GBS can be simulated by
decorating the GB structure under different
misorientation conditions with
these defects.
Microstructure-based Model for
Elevated Temperature Deformation
A microstructure-based model to
predict the elevated temperature flow
stress in polycrystalline aluminum as a
function of grain size, T, and 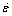 26,27 has
been developed. The model, which incorporates
GBS, grain boundary diffusion,
and dislocation creep is illustrated
in Figure 6a. A representative volume
element of polycrystalline AA5083 is
idealized as a collection of grains, separated
by grain boundaries. Each grain
is modeled as an f.c.c. single crystal,
which deforms by dislocation creep. A
standard elastic-plastic crystal plasticity
model is used to model deformation
in the grains. Grain boundaries permit
adjacent grains to slide relative to one
another in response to the resolved
shear stress acting on the boundary, and
can also act as paths for grain boundary
diffusion. 26,27 has
been developed. The model, which incorporates
GBS, grain boundary diffusion,
and dislocation creep is illustrated
in Figure 6a. A representative volume
element of polycrystalline AA5083 is
idealized as a collection of grains, separated
by grain boundaries. Each grain
is modeled as an f.c.c. single crystal,
which deforms by dislocation creep. A
standard elastic-plastic crystal plasticity
model is used to model deformation
in the grains. Grain boundaries permit
adjacent grains to slide relative to one
another in response to the resolved
shear stress acting on the boundary, and
can also act as paths for grain boundary
diffusion.
The predicted variation of flow stress
with strain rate for AA5083 with several
different grain sizes is compared with experimental measurements in
Figure 6b. The model predicts behavior
that is in good agreement with our experiments:
at strain rates above 10–3 s–1,
the dominant deformation mechanism
is solute drag creep, and consequently
the stress exponent n approaches 4. At
low strain rate, grain boundary sliding
provides the dominant contribution to
the total strain, so the stress exponent
drops to n–2.
The flow stresses predicted by this
model can be fit by phenomenological
constitutive equations for Al-Mg
alloys that accounts for two-independent
creep mechanisms,28,29 as shown
in Equation 12, where b is the Burgers
vector, d is the grain size, τ is applied
stress, τo is the threshold stress
for grain boundary sliding, Q is the
activation energy, n is the stress exponent,
T is the temperature, R is the
gas constant, and E is the temperature
compensated modulus. The subscript
1 refers to constants associated with
grain boundary sliding, while subscript
2 refers to constants associated
with dislocation creep. This constitutive
equation is then used in finite element
simulations of manufacturing
processes of interest, for example, the
dome height reached by a specimen
in a simple, biaxial gas pressure dome
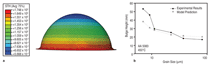
forming experiment.30 Figure 7 compares
the measured and predicted dome
heights for materials with several grain
sizes. The model predicts behavior that
is in excellent agreement with experiments,
with a small discrepancy for the
material with grain sizes below 10 μm.
The method has also been shown to
successfully predict the location and
extent of thinning during forming of a
more complex three-dimensional closure
component.31
Material Design Opportunities and Challenges
One key opportunity for elevated
temperature material design is to enhance
GBS in relatively coarse grains.
Previous research has determined that
optimum forming occurs when GBS
and dislocation creep contribute equally
to deformation. Using the microstructure-
based model, we have studied
the effect of varying the threshold
stress for GBS (τo)32 and grain boundary
misorientation induced heterogeneity33 on elevated temperature flow. The
results showed that the critical strain
rate at which the deformation mechanism
transitions from GBS to dislocation
creep increases with the fraction of
free sliding boundaries, thus suggesting
improved forming.
We have performed simulations using
the NEMD model to explore how
magnesium and silicon additions affects
τo.34 As shown in Figure 5b, magnesium
solutes increased τo of all grain
boundaries because they formed immobile
clusters with surrounding aluminum
atoms due to the negative heat
of formation of magnesium and aluminum.
However, silicon solute atoms
decreased (by approximately a factor
of two) the sliding threshold in lowenergy
grain boundaries by weakening
aluminum bonds, increasing the mobility
of the surrounding aluminum atoms,
and consequently enhancing grain
boundary diffusivity. To demonstrate
the potential impact of modifying the
grain boundary composition, we used
the microstructure-based model for elevated
temperature flow and assumed
that adding silicon decreased the percentage
of non-sliding boundaries from
43% to 23%. If we applied a stress of
10 MPa to the system, the resulting
strain rate increased from 1.2Χ10–3 to
2.2Χ10–3s–1, which translates to faster
cycle times and lower cost forming.
The results above show that it is
possible to use a microstructure-based
model to compute parameters needed
in finite element forming simulations
of elevated temperature forming. The
model provides the framework for a
multi-scale computational approach
so that we can design materials for improved
formability and rapidly evaluate
them in a forming operation. Ideally,
values for the key parameters in
the model should be determined from
atomic scale models, but at present,
atomic-scale models do not provide a
fully quantitative description of elevated
temperature flow behavior. For example,
recent atomistic models which
account in detail for the behavior of
solutes in the dislocation core35 predict
that the solute drag exponent n=3, different
from experimentally determined
n=4. The discrepancy is likely to be a
consequence of over-simplifying the
behavior of dislocations in the models, in which
neglect climb, and assume all
dislocations move at their steady-state
velocity. Similarly, MD simulations
predict a large τo for GBS and very
high sliding velocities when τo is exceeded,
compared to the macroscopic
flow stresses observed experimentally
during elevated temperature forming.
MD simulations are likely to correctly
predict the qualitative influence
of GB structure on τo but quantitative
predictions will require simulations
over time-scales that greatly exceed
the capability of current MD simulations.
Obtaining quantitative predictions
of grain boundary diffusivity
from atomic scale computations poses
similar challenges. The complexity of
grain boundary structure also hinders
generalizing and passing information
from MD simulations to microstructure
based FEM simulations. For example,
microstructural information about
grain boundary typically only contains
mis-orientation angle, however grain
boundary structures have five degrees
of freedom. The grain boundary structures
for alloys may even require new
theories that treat the grain boundary
as a separated phase, whose properties
are orientation, atomic disordering, and
chemistry dependent.36
Even at the molecular level, describing
atomic interactions by accurate
alloy atomic potentials still remains a
great challenge. Due to the limitation
of empirical potentials (availability,
transferability, and accuracy), a general
strategy for evaluating the influence
of arbitrary solute atoms on GBS (or
other deformation mechanism) should
be using MD simulations with empirical
potentials to identify critical atomic
scale parameters that control GBS resistance.
Then, more accurate quantum
mechanics computations (such as
DFT) can be used to identify solutes
with the relevant properties. For example,
the connection between heat of
formation and bonding strength to τo
indicates that the heat of formation can
be used as a guide for grain boundary
engineering. Heat of formation can be
easily computed from more accurate
DFT calculations37–39 or measured from
experiments.40
In view of the difficulties in quantifying
creep mechanisms at the atomic
scale, at present parameters in our microstructure
based model must be determined
primarily from experiments.
The parameters can be determined by
measuring the flow stress of an aluminum
alloy as a function of strain rate, for a single grain size. Further work will
be required to develop accurate quantitative
predictions of creep mechanisms
at the atomic scale, before a fully predictive
model of the effects of material
composition on elevated temperature
formability will be possible. Although,
the microstructure level model continues
to rely on some experimental
calibration, it demonstrates that incorporating
grain boundary structures, orientations,
energies, defects (such as vacancy
and solute atoms) dependence of
the key GBS parameters (τo and η) into
the microstructure based FEM forming
modeling could ultimately lead to
microstructure optimization and novel
material processing design.
CONCLUSTION
The multi-scale methodology described
in this paper provides an approach
for obtaining accurate constitutive
laws based on physical phenomena
that influence metal plasticity. The
computational techniques developed
also fill the critical gap when experimental
data to calibrate the existing
constitutive laws are not readily available.
However, the computational
methods are still not sufficiently developed
or efficient enough that information can seamlessly fl ow from
the atomic to the continuum scale to
allow for an embedded approach to
metal plasticity. The success of the hierarchical
approach thus used is critically
dependent on the validation of
the models at each length scale against
well designed experiments. A key area
of future research will be to formulate
homogenization strategies at each
length scale to allow selective fl ow
of information, with special emphasis
on the transition from the atomistic
description to the grain-level three dimensional
(3-D) microstructure that
is the realm of materials engineering. It
is expected that implementing accurate
and calibrated hardening laws in fi nite
element models, which accurately account
for 3D microstructure and the
physical deformation mechanisms,
will ultimately contribute to better material
usage and also provide a predictive
tool for developing materials with
improved performance;in concert with
the vision of "Atoms to Autos"!
ACKNOWLEDGEMENTS
The authors gratefully acknowledge
support of this work by the General
Motors/Brown Collaborative Research
Laboratory on Computational Materials
Science. Computational resources
and technical support were provided
by GM Information Systems and Services.
S. Chakravarthy kindly provided
the authors with Figure 3a,b.
References
- R.A. Ayres, Metall. Trans. A, 10A (1979), pp. 849854.
- W.H.L. Hooper, J. Institute of Metals, 81 (1952), pp. 563568.
- G. Kresse and J. Furthmόller, Comput. Mat. Sci., 6
(1996), pp. 1550.
- C. Woodward and S. Rao, Phys. Rev. Lett., 88
(2002), pp. 216402,14.
- J. Hafner, J. Phys.: Condens. Matter, 22 (2010), pp.
384205,112.
- G.P.M. Leyson, W.A. Curtin, L.G. Hector, Jr., and C.F.
Woodward, Nature Materials, 9 (2010), pp. 750755.
- B.J. Diak and S. Saimoto, Mater. Sci. Eng. A, 234
(1997), pp. 10191022.
- B.J. Diak, K.R. Upadhyaya, and S. Saimoto, Prog.
Mater. Sci., 43 (1998), pp. 223363.
- W.A. Curtin, D.L. Olmsted, and L.G. Hector, Jr., Nature
Materials, 5 (2006), pp. 875880.
- S. Kok, M.S. Bharathi, A.J. Beaudoin, C. Fressengeas,
G. Ananthakrishna, L.P. Kubin, and M. Lebyodkin,
Acta Materialia, 51 (2003), pp. 36513662.
- M.A. Soare and W.A. Curtin, Acta Materialia, 56
(2008), pp. 40464061.
- F. Zhang, A.F. Bower, and W.A. Curtin, Int. J. Numerical
Methods in Eng., 86 (2011), pp. 7092.
- T. Rasmussen, T. Vegge, T. Leffers, O.B. Pedersen,
and K.W. Jacobsen, Phil. Mag. A, 80 (2000), pp.
12731290.
- G.I. Taylor, J. Inst. Met., 62 (1938), pp. 307325.
- W.T. Koiter, Quart. Appl. Math., 11 (1953), pp.
350354.
- D. Peirce, R.J. Asaro, and A. Needleman, Acta
Metall., 31 (1983), pp. 19511976.
- J. Rossiter, A. Brahme, M.H. Simha, K. Inal, and R.K. Mishra, Int. J. Plasticity, 26 (2010), pp. 17021725.
- K.P. Boyle, Materials Science Forum, 495-497(2005), pp. 10431048.
- K.H. Kim and Y.M. Koo, J. Mater. Sci. Letters, 20 (2001), pp. 625627.
- A. Brahme, P. Abhijit, K. Inal, R.K. Mishra, and S. Saimoto, Computational Materials Science, 50 (2011), pp. 28982909.
- F. Zhang, A.F. Bower, R.K. Mishra, and K.P. Boyle, Int. J. Plasticity, 25 (2009), pp. 4969.
- nominally binary Fe ppm.
- A.I. Taub, P.E. Krajewski, A.A. Luo, and J.N. Owens, JOM, 59 (2) (2007),
pp. 4857.
- Y. Qi and P.E. Krajewski, Acta Materialia, 55 (2007), pp. 15551563.
- N. Du, Y. Qi, P.E. Krajewski, and A.F. Bower, Acta Materialia, 58 (2010), pp. 42454252.
- A.F. Bower and E. Wininger, J. Mechanics and Physics of Solids, 52 (2004), pp. 12891317.
- S. Agarwal, C.L. Briant, P.E. Krajewski, A.F. Bower, and E.M. Taleff, J. Mater. Eng. Perform., 16 (2007), pp. 170178.
- M.A. Kulas, W.P. Green WP, E.M. Taleff, P.E. Krajewski, and T.R. McNelley, Metall. Mater. Trans. A, 36 (2005), pp. 12491261.
- W.P. Green, M.A. Kulas, A. Niazi, K. Oh-ishi, E.M. Taleff, and P.E. Krajewski, Metall. Mater. Trans. A, 37 (2006), pp. 27272738.
- J.R. Bradley, Superplasticity and Superplastic Forming, ed. E.M. Taleff, P.A. Friedman, P.E. Krajewski, R.S. Mishra, and J.G. Schroth (Warrendale, PA: TMS,
2004), pp. 109118.
- P.E. Krajewski, L.G. Hector, Jr., N. Du, and A. Bower, Acta Materialia, 58 (2010), pp. 10741086.
- N. Du, A.F. Bower, P.E. Krajewski, and E.M. Taleff, Mater. Sci. and Eng. A, 494 (2008), pp. 8681.
- D. Cipoletti, A. Bower Y. Qi, and P.E. Krajewski, Mater. Sci. and Eng. A, 504 (2009), pp. 175182.
- N. Du, Y. Qi, P.E. Krajewski, and A.F. Bower, Metall. Mater. Trans. A, 42 (2011), pp. 651659.
- F. Zhang and W.A. Curtin, Mater. Sci. and Eng., 16
(2008), pp. 118.
- S.J. Dillon, M. Tang, W.C. Carter, and M.P. Harmer,Acta Materialia, 55 (2007), pp. 62086218.
- N. Chetty, M. Weinert, T.S. Rahman, and J.W. Davenport, Phys. Rev. B, 52 (1995), pp. 63136326.
- B. Jelinek, J. Houze, S. Kim, M.F. Horstemeyer, M.I. Baskes, and S.G. Kim, Phys. Rev. B, 75 (2007), 19.
- Y. Mishin, W.J. Boettinger, J.A. Warren, and G.B. McFadden, Acta Materialia, 57 (2009), pp. 37713785.
- J.R. Davies, ASM Specialty Handbook: Aluminum
and Aluminum Alloys (Materials Park, OH: ASM International,
1993), pp. 579580.
P.E. Krajewski, engineering group manager and
technical fellow, L.G. Hector, Jr., technical fellow,
Y. Qi, staff research scientist, R.K. Mishra, technical
fellow, and A.K. Sachdev, research fellow
and lab group manager, are with General Motors
Company, Warren, MI 48090; A.F. Bower, professor
of engineering, and W.A. Curtin, Elisha Benjamin
Andrews Professor, are with Brown University,
School of Engineering, Providence, RI 02912. Dr.
Krajewski can be reached at paul.e.krajewski@
gm.com.
|