TMS QUICK LINKS:
  • TMS ONLINE
  • MEMBERS ONLY
  • MEMBERSHIP INFO
  • MEETINGS CALENDAR
  • PUBLICATIONS

JOM QUICK LINKS:
  • JOM HOME PAGE
  • MORE HTML ARTICLES
  • COMPLETE ISSUES
  • BOOKS REVIEWS
  • SUBSCRIBE

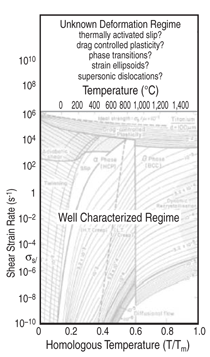
In recent years a powerful experimental tool has been added to the arsenal at the disposal of the materials scientist investigating materials response at extreme regimes of strain rates, temperatures, and pressures: laser compression. This technique has been applied successfully to mono-, poly-, and nanocrystalline metals and the results have been compared with predictions from analytical models and molecular dynamics simulations. Special flash x-ray radiography and flash x-ray diffraction, combined with laser shock propagation, are yielding the strength of metals at strain rates on the order of 10⁷–10⁸ s^–1 and resolving details of the kinetics of phase transitions. A puzzling result is that experiments, analysis, and simulations predict dislocation densities that are off by orders of magnitude. Other surprises undoubtedly await us as we explore even higher pressure/ strain rate/temperature regimes enabled by the National Ignition Facility.

INTRODUCTION

Ever since the discovery of lasers in the 1950s their interactions with materials have been explored. Laser welding, cutting, surface treatment, and heat treatment of metals are well established technologies which are highly successful. By far the most important application of lasers is in optical storage devices. The power of lasers ranges from less than 1 mW (for a common laser pointer) to 700 TW—the combined energy of 192 laser beams focused on a minute 2–3 mm diameter target at the National Ignition Facility at Lawrence Livermore National Laboratory (LLNL) in Livermore, California.¹ It was realized early that lasers can also produce shock waves in materials. As early as 1963, Askaryon and Morez² demonstrated that shock pulses could be generated in metals from laser-pulseinduced vaporization at the surface.

The use of surfaces covered by a lasertransparent overlay was introduced by Anderholm;³ this enabled the confinement of the vapor products, resulting in an increase of the peak pressure of the shock launched into the metal. Shock amplitudes as high or higher than those generated by explosives or planar impact devices could be generated with a fundamental difference: the duration of the shock pulse was in the nanosecond range. 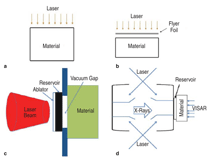In the 1980s Clauer et al.⁴ used these laser-induced shock pulses to modify the structure of engineering alloys, increasing their strength and fatigue resistance.

The recent National Research Council report titled “Frontiers in High Energy Density Physics: The X-Games of Contemporary Science” presents the immense challenges facing science as the extreme regimes of pressure, strain rate, and temperature are explored.⁵ The schematic diagram shown in Figure 1 is a Weertman-Ashby plot for titanium in which the temperature and strain rate are plotted. The conventional (i.e., known) and extreme (unknown) deformation rate regimes are marked. The bottom part of the plot (below 10⁶ s^–1) is the well-characterized region in which deformation takes place by dislocations, twinning, or diffusional processes. The different regimes have been extensively studied and are part of the body of knowledge of materials science and engineering.

The extreme regimes of pressure, temperature, and strain rates that comprise the top portion of the plot can only be accessed through very special methods. Although the fi rst fundamental investigation, by C.S. Smith,⁶ was carried out approximately 60 years ago, this remains a frontier area. For strain rates from 10⁶ to 10¹⁰ s^–1, deformation mechanisms are less well understood and conventional deformation mechanisms are not applicable. An additional complexity is introduced by nanostructured metals, in which the mechanisms of plastic deformation are significantly different. Compression by high-power lasers is one of the methods through which we can access these extreme regimes.

LASER-MATERIAL INTERACTION

Laser-induced shock waves can be launched by several techniques; Figure 2 shows two more traditional and two novel methods to illustrate the experimental choices. Figure 2a shows the direct incidence of laser energy on the surface of the metal. The energy deposited onto the metal surface causes it to vaporize. The vapor pressure creates a pressure pulse into the metal specimen. Alternatively, lasers can be used to accelerate a foil onto the target, generating a shock wave of square shape in this manner (Figure 2b). The difference in the duration of the pulse between lasers and gas gun or explosively driven flyer plates is on the order of 100 or more. To access very high pressure regimes of material deformation and lattice dynamics, it is desirable to increase the pressure to as high a level as possible without melting the target. A slower compression rate, called quasi-isentropic compression, presents a definite advantage over the sharp shock compression, with a strain rate at the front that is orders of magnitude lower.

This quasi-isentropic compression can be accomplished by using a reservoir, shown in Figure 2c. This acts as a ‘pillow’ that softens the blow of the laser.^7–9 A fourth method uses the Hohlraum effect (Figure 2d). This is a German word that means ‘hollow cavity.’ It is the principle of energy deposition of the National Ignition Facility and will be described in a later section. In essence, it enables the generation of x-rays which illuminate the target in a more uniform manner. The lasers converge into the Hohlraum and deposit their energy on the internal walls, heating them up until they glow in the soft x-ray spectral regime, creating a mini-radiation chamber which then launches a shock into the sample being studied. These x-rays are the primary source of energy deposition onto the specimens.

The lasers used to produce shock waves are high-amplitude pulses that have a tailored shape. The laser source with sufficient energy to launch these single pulses is usually a glass laser. The laser energy used in current experimental facilities varies from 10 J/mm² to 1 kJ/mm² with durations that typically vary between 1 and 10 ns. On NIF, the energies can go much higher. Figure 3 shows a typical laserinduced pressure wave propagating in a sample of vanadium. The pressure decays rapidly as the pulse travels and dissipates. It can be seen that after propagating 0.25 mm the amplitude of the pulse is a small fraction of the initial value.

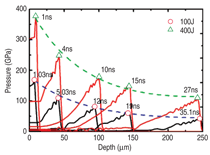
This rapid decay of the pulse presents an advantage in ‘freezing in’ the structural changes introduced by the pulse, since it acts as a self-quenching mechanism. In gas gun and explosive experiments the postshock temperature of the samples can rise easily to levels where recovery and recrystallization occur, destroying the effects that we want to study. The lateral dimensions of the laser beam are small in comparison with gas gun and explosive experiments—a few mm versus 100–300 mm. However, these dimensions are sufficient to extract specimens for characterization by transmission electron microscopy.

Lasers and molecular dynamics simulations are well suited for each other, since they both occur at high strain rates (~10⁸ s^–1). This is even more accentuated if nanocrystalline metals are investigated because the size of grains that can be modeled in molecular dynamics is in the nanometer range. Thus, the comparison of structures characterized by transmission electron microscopy (TEM) from laser recovery experiments with molecular dynamics (MD) simulations is a fertile ground for research.

An illustration of this is shown in Figure 4a, which is a schematic of a propagating shock front and partial dislocation loops generated and growing behind it. The shock stress is often in the regime in which dislocations can be homogeneously generated (pressure > shear modulus/10). Thus, a dense network of dislocations is developed. These can be perfect dislocations, leading to the formation of cellular structures, or partial dislocations, leading to stacking faults, as those observed in Figure 4b.

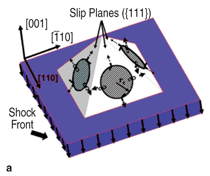
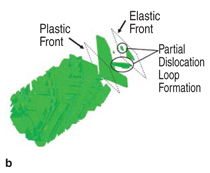
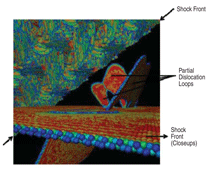
The formation of these defects can be modeled by molecular dynamics, and the results are shown in Figure 5.¹⁰ A section through the simulation box in Figure 5a shows the parallel lines which are stacking faults. The formation of these stacking faults through the generation and expansion of partial dislocation loops is shown in Figure 5b. The density of these loops increases behind the shock front. 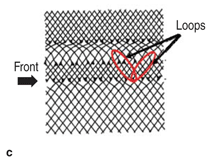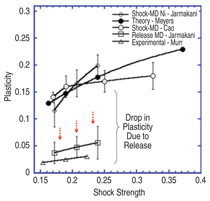The formation of these loops is complex, with schematic pictures already advanced early on, as shown in Figure 5c.¹¹ We note that the leading edge of partial loops can develop velocities close to the bulk sound velocity, at this high stress and when not pulled back by a trailing partial dislocation.

The dramatic picture of Figure 6 shows both dislocation nucleation at a pre-existing dislocation loop and the homogeneous dislocation nucleation front for a ramped shock propagating through a copper specimen.¹² Approximately 350 million atoms were used in the simulation. Only the atoms disturbed from their original face-centered cubic (f.c.c.) lattice position are imaged. The broad view of the front shows, in a section, the intense dislocation activity generated by the propagation of the shock front at pressures beyond the homogeneous nucleation limit, producing mostly partial loops with only the leading partial produced. The close view shows, in perspective, how dislocation loops are nucleated at a pre-existing defect. These are partial dislocations, the leading partial being followed by the trailing, which recomposes the perfect f.c.c. structure. This explains the ‘hole’ in the core of the loops imaged in the right-hand side of Figure 6. These dramatic representations can lead to quantified predictions of dislocation densities.

The plot shown in Figure 7 presents the shock strength (related to the maximum stress) as a function of the plasticity (related to the dislocation density). This is the so-called Holian–Lomdahl plot.¹³ As expected, the plasticity increases with the shock strength, since dislocation density is directly related to the pressure. The results from simulations by Cao et al.¹⁴ for copper and Jarmakani et al.¹⁰ for nickel are shown in the top of Figure 7, together with the analytical predictions from the homogeneous dislocation model. The comparison of these computed dislocation densities with experimentally measured (through TEM) densities and with an analytical homogeneous dislocation theory provided a puzzling surprise: the predictions from molecular dynamics (MD) and theory are orders of magnitude higher than the experimentally measured values.

Although results by Murr¹⁵ are shown, extensive TEM work by other groups confirm these low (in comparison with MD and theoretical predictions) dislocation densities (expressed as plasticity in Figure 7; see caption for relationship between the two) (e.g., Bourne et al.¹⁶). Murr and Kuhlmann–Wilsdorf¹⁷ had predicted an empirical relationship of the form between the pressure, P, and dislocation density, π, based on experimental measurements of dislocation cell sizes: π α P^1/2. Figure 7 shows that the experimental results, in the bottom of the plot, follow the same trend as the MD simulations and theory, but are lower by orders of magnitude. This difference is not yet completely understood, but three effects play a role, separately or jointly:¹⁸

1. The strain rate at the shock front in MD simulations is extremely high. The shock wave propagates into an ideal lattice devoid of dislocations. Thus, the deviatoric stress is integrally accommodated by homogeneous dislocation loop generation. In real experiments, the strain rate at the front is lower and there is an existing network of dislocations, which can accommodate some of the stresses through motion.
2. Molecular dynamics simulations (marked Release-Jarmakani) show a dramatic decrease in dislocation density upon unloading. This is shown in Figure 8. A fraction of these loops can shrink upon unloading if no cross-slip has taken place since the deviatoric stresses are removed. When this occurs, the dislocation density decreases. The dislocation configurations at the peak stress and after unloading are shown in Figure 8. The green regions are stacking faults. This decrease in dislocation density corresponds to a decrease in plasticity. The results for calculations at three maximum pressure levels are plotted in Figure 7. The arrow in the plot represents the drop in plasticity due to unloading (also called ‘release’ in shock jargon).
3. Thermal recovery: even the release simulations shown in Figure 7 only last a fraction of a nanosecond. However, thermal effects lasting up to microseconds might lead to dislocation rearrangement and reactions that would likely decrease the net dislocation density. Such effects could be partly explored by dislocation dynamics simulations or other physically based plasticity models informed by experiments and atomistic simulations.

This and many other issues are not yet resolved, and laser experiments combined with molecular dynamics simulations and physically based models will shed light on the deformation mechanisms in these extreme regimes. Of particular importance are flash x-ray diffraction experiments which can probe the shocked state and infer the defect structure during the laser compression process. These experiments are currently being carried out by Wark and coworkers at Oxford University, U.K.,^19,20 using the Vulcan Laser facility, and by Hawreliak et al.,²¹ and Milathianaki and McNaney et al.²² at LLNL using the Omega and Janus facility.

Another new technique is to use flash x-ray radiography to observe the rate of material deformation driven by buoyancy-type hydrodynamic instabilities. This new experimental technique allows material strength to be inferred at very high pressures and strain rates.^23,24 This technique will be developed on the NIF laser, where samples in the solid state can be studied at extraordinary pressures, P > 103 GPa, approaching those found, for example, at the centers of the giant planets.^7,25

The experimental facilities of Omega (Laboratory for Laser Energetics, University of Rochester, New York), Jupiter (LLNL), Trident (Los Alamos National Laboratory), and Vulcan (U.K.) enable unique materials experiments. These facilities have been and are being successfully used to explore the extreme material regimes not accessible by other shock wave means such as explosive detonation and gas gun impact. The National Ignition Facility at LLNL will provide a much higher energy deposition capability. As we embark on the NIF era, it is imperative to understand the basic physics of plastic deformation of advanced materials in the extreme regimes created under these conditions. The National Ignition Facility Program at LLNL is designed to provide:

• Energy: demonstrate fusion ignition and energy gain—the first step toward limitless fusion power production.
• National security: understand the complex underlying physics of nuclear weapons, ensuring the safety and reliability of the country’s stockpile.
• Basic science: NIF experiments can create immense pressures and temperatures similar to those in planetary interiors, stars, and supernovae, shedding light on astrophysical phenomena, materials science and nuclear physics.²⁶

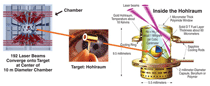
The National Ignition Facility is massive, with 192 high-power laser beams designed to be fired simultaneously and focused on a capsule. Figure 9 shows an overall view of the facility, which occupies an area equivalent to approximately four football fields. These 192 laser beams converge onto a chamber having approximate diameter of 10m (Figure 10). Precise timing of the beams has to be ensured to within ~50 ps. These beams enter a hollow cylinder, the Hohlraum, interact with the walls and generate the intense xrays that illuminate the capsule (Figure 11). Direct incidence of the laser beams onto the hollow capsule is less uniform and can create instabilities in the compression process. The capsule, which contains the fusion material (a solid deuterium layer with 80 μm thickness), is compressed from its initial diameter of 2 mm to approximately 0.5 mm. At that point fusion burn should take place, generating more energy than the combined energy of the laser beams.

Laser-induced shocks and isentropic compression are new and powerful research tools to investigate the behavior of materials under extreme conditions. The processes of plastic deformation, fracture, and fragmentation under these conditions are still poorly known. Many questions remain to be explored using the powerful experimental capabilities, instrumentation and diagnostic tools, computational and analytical techniques, and advanced characterization methods.

1. C.A. Haynam et al., Appl. Optics, 46 (2007), p. 3276.
2. G.A. Askarion and E.M. Morez, JETP Lett., 16 (1963), p. 1638.
3. N.C. Andelholm, Appl. Phys. Lett., 16 (1970), p. 113.
4. A.H. Clauer et al., Shock Waves and High-Strain- Rate Phenomena in Metals, ed. M.A. Meyers and L.E. Murr (New York: Plenum Press, 1981), pp. 675–702.
5. R.C. Davidson et al., Frontiers in High Energy Density Physics: The X-Games of Contemporary Science, (Washington, D.C.: The National Academies Press, 2003).
6. C.S. Smith, Trans. AIME, 212 (1958), p. 574.
7. B.A. Remington et al., Met. Mat. Trans., 35A (2004), pp. 2587–2608.
8. H.S. Park et al., J. of Phys.: Conf. Ser., 112 (2008), 042024.
9. R.F. Smith et al., Phys. Plasmas, 14 (2007), 057105.
10. H.N. Jarmakani et al., Acta Mat., 56 (2008), p. 5584.
11. M.A. Meyers, Scripta Met., 12 (1978), p. 21.
12. E.M. Bringa et al., Nature Materials, 5 (2006), p. 805.
13. B.L. Holian and P.S. Lomdahl, Science, 2890 (1998), p. 2085.
14. B.Y. Cao, E.M. Bringa, and M.A. Meyers, Met. Mat. Trans., A38 (2007), p. 1073.
15. L.E. Murr, Shock Waves and High-Strain-Rate Phenomena in Metals, ed. M.A. Meyers and L.E. Murr (New York: Plenum Press, 1981), p. 607.
16. N.K. Bourne, J.C.F. Millet, and G.T. Gray, J. Matls. Sci., 44 (2009), pp. 3319–3343.
17. L.E. Murr and D. Kuhlmann-Wilsdorf, Acta Met., 26 (1978), p. 847.
18. M.A. Meyers et al., Dislocations in Solids, ed. J.P. Hirth and L.P. Kubin (Maryland Heights, MO: Elsevier, 2009), pp. 94–197.
19. J.S. Wark et al., Phys. Rev., B40 (1989), p. 5705.
20. J.S. Wark et al., SCCM-2007, Vol. 955 (2007), p. 1345.
21. J. Hawreliak et al., Phys. Rev. B, 78 (2008), 220101(R).
22. D. Milathianaki and J.M. McNaney et al., Rev. Sci. Instrum., 80 (2009), 093904.
23. H.S. Park et al., Phys. Rev. Lett., submitted (2009).
24. H.S. Park et al., Phys. Plasmas, submitted (2009).
25. B.A. Remington et al., Mat. Sci. Tech., 22 (2006), p. 474.
26. E.I. Moses et al., Phys. Plasmas, 16 (2009), 041006.
27. Lawrence Livermore National Labs Report, LLNLAR- 412551 (2009).

M.A. Meyers is at the University of California, San Diego; B.A. Remington and B. Maddox are with Lawrence Livermore National Lab.; and E.M. Bringa is with the Universidad Nacional de Cuyo, Argentina. Dr. Meyers can be reached at mameyers@ucsd.edu.