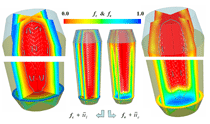LATEST ISSUE |
||||
TMS QUICK LINKS: |
• TECHNICAL QUESTIONS • NEWS ROOM • ABOUT TMS • SITE MAP • CONTACT US |
JOM QUICK LINKS: |
• COVER GALLERY • CLASSIFIED ADS • SUBJECT INDEXES • AUTHORS KIT • ADVERTISE |
|
| Research Summary: JOM-e: Visualization: Defects in Casting Processes | Online Only |
Modeling Macrosegregation with a
Multiphase
Approach: Examples and Discussions
Menghuai Wu and Andreas Ludwig
| ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
|
|
||||||||||||||||
Questions? Contact jom@tms.org. © 2006 The Minerals, Metals & Materials Society |
|
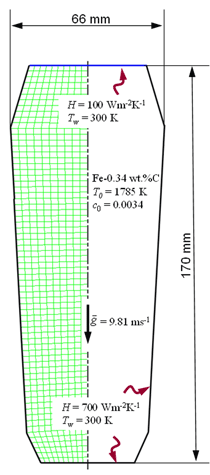
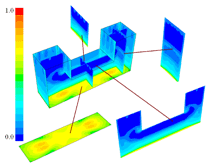
INTRODUCTION Knowledge of macrosegregation phenomena in castings has increased significantly in the past few decades, including the development of different analytical and numerical models to study and predict such phenomena in different casting processes.1–3 Macrosegregation occurs due to the relative motion between different phases during solidification. This motion can arise as a result of thermosolutal convection, solidification-shrinkage-induced flow, flotation and sedimentation of free-moving grains, forced flow by stirring mechanically or electromagnetically, flow caused by pore or gas bubble formation, deformation of the solid framework, capillary (Marangoni) force induced flow, etc.1–5 As summarized by C. Beckermann: “while some successes have been reported in predicting measured macrosegregation patterns in industrially relevant casting processes, there are still numerous areas where further development is required.”2 Obviously, this article cannot cover the entire range of macrosegregation phenomena, thus the current focus is limited to the authors’ recent contributions to this topic. As such, specific examples of macrosegregation in columnar solidification, in globular equiaxed solidification, in mixed equiaxed-columnar solidification, and Marangoni-induced macrosegregation are presented and discussed. Details about the numerical models are presented elsewhere.6–10 MACROSEGREGATION IN COLUMNAR SOLIDIFICATION The benchmark of a steel ingot with reduced size is simulated in Figure 1. A two-phase columnar solidification model is used. The purpose is to study the macrosegregation due to the mechanism of thermosolutal convection during columnar solidification. Details about process and thermo-physical parameters can be found in previous publications.5,8 The important model assumptions are summarized as follows:
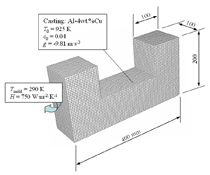
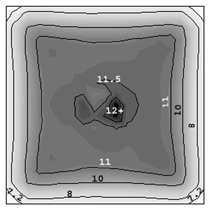
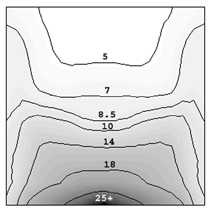
The solidification process is shown in Animation 1. Columnar trunks start to grow from mold wall and the columnar tip front advances from the mold wall toward the bulk melt. Due to the influence of the thermosolutal convection, the ‘hot spot’ moves upward and is finally located above the geometrical and thermal center of the casting. During solidification two axis-symmetric convection vortices develop. The melt near the mold wall has a higher density due to its lower temperature (ΒT = 2 × 10–4 K–1) and sinks downward. The hotter melt in the center rises. One may argue that the solute-enriched interdendritic melt might partially compensate or reverse the above-mentioned convection pattern. The liquid concentration cl near the mold wall is much higher compared to the bulk melt region. With Βc = 1.1 × 10–2 wt.%–1, the higher the cl, the lighter the interdendritic melt. Due to the high temperature gradient in the casting, however, the thermal buoyancy has a greater impact on the fluid motion than the solutal buoyancy. The downward flow in the interdendritic regions and the upward flow in the bulk melt are the basic phenomena that lead to the formation of the final macrosegregation pattern. The positive macrosegregation in the center is formed gradually during solidification. The interdendritic melt always has a higher concentration than the bulk melt. The interdendritic solute-enriched melt is brought out of the mushy zone by the flow current, causing the cmix in front of, or slightly behind, the columnar tip front to be enriched gradually. These positively segregated areas of the melt are not stationary; they move with the flow current and finally meet in the casting center, forming a large positive segregation zone. The benchmark of an Al-4.0wt.%Cu die casting with a two-phase globular equiaxed solidification model is simulated, as shown in Figure 3. The purpose is to study the macrosegregation formed by mechanisms of grain sedimentation, and sedimentation-induced convection during equiaxed solidification. Details about process and thermophysical parameters can be found in previous publications.6.12 The general model descriptions and assumptions are:
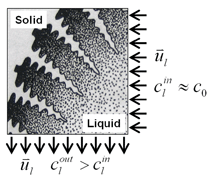
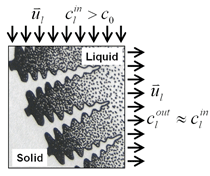
A three-dimensional (3-D) overview of the equiaxed phase distribution at 10 s after the start of cooling is shown in Figure 4. The dynamic evolution sequences of the equiaxed phase, the sedimentation, and the induced macrosegregation are demonstrated in Animation 2. Grains which nucleate in the upper regions and at the sidewalls sink downward. The sinking grains lead to an accumulation of the solid phase in the bottom region of the casting. The grains stop moving and finally settle when the local fraction of solid exceeds the packing limit (0.637). The grain settlement is the main reason for the negative segregation at the bottom of the casting. As solidification proceeds, this negative segregation zone becomes wider and wider. The strongest negative segregations are found in the lower corners near the sidewalls, where the grains tend to accumulate and settle. As the residual positively segregated melt is separated from the sedimentation zone by the settling of grains, a positive segregation zone is formed nearby. It is generally observed that a positive segregation zone exists just near a sedimentation zone. This positively segregated zone is located within the melt, thus it is not stationary and may move with the melt flow. While solidification proceeds, the positively segregated melt areas move toward and accumulate gradually in the last-to-solidify region, forming a large positively segregated zone in the late stage of solidification. When the same benchmark as Figure 1 was simulated and a 3-D calculation carried out, the benchmark showed a complex case of macrosegregation formation with the mechanisms of coupled thermosolutal convection, grain sedimentation, and sedimentation induced convection. Details about process and thermo-physical parameters can be found in previous publications.8 The important model assumptions are:
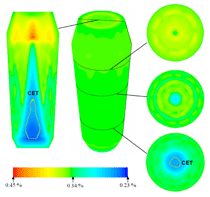
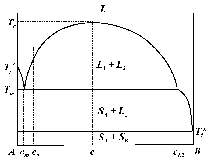
The simulated solidification sequence including sedimentation of the equiaxed grains, sedimentation-induced melt convection, and thermosolutal melt convection are shown in Figure 5 and Animation 3. The solidification pattern agrees with the classical explanation of steel ingot solidification, summarized by J. Campbell.14 The columnar dendrites grow from the mold wall and the columnar tip front moves inward. The equiaxed grains nucleate near the mold walls and in the bulk melt. The columnar dendrites are stationary, whereas the equiaxed grains sink and settle in the base region of the ingot. The accumulation of such grains at the base of the ingot has a characteristic cone shape. Two symmetrical melt convection vortices in the ingot are induced by both thermosolutal effects and the drag of sinking grains. The sedimentation of grains and occurring melt convection influence the macroscopic solidification sequence and thus, the final phase distribution: more equiaxed grains will be found at the bottom and in the base region, and larger columnar areas in the upper part of the ingot. The multiphase solidification approach discussed above is applied to model the spatial phase separation and macrosegregation caused by thermo-capillary force-induced convection (i.e., Marangoni) convection in a hypermonotectic alloy. As shown in Figure 7, when a hypermonotectic alloy with initial concentration c0 is cooled down below the binodal, a secondary liquid phase (L2) is decomposed in the form of droplets from the parent melt (L1). The surface tension between L1 and L2 is a function of the temperature. Therefore, due to the temperature gradient during solidification local convections inside and around the droplet are established. As a consequence, this thermo-capillary force-induced convection leads to the droplet moving from cold toward hot regions. A 2-D benchmark of Al-10.wt.%Bi alloy with a square cross section is simulated and during solidification, as shown by the phase diagram (Figure 7), at least four phases appear: the parent melt L1, the secondary liquid phase L2, the solidified monotectic matrix, and the solidified secondary phase. For simplicity the authors’ approach considers only two phases: L1 and L2. During monotectic reaction the monotectic matrix is transformed directly from L1. Therefore the solidified monotectic matrix is modeled as phase L1 in such a way that an enlarged viscosity is applied to phase L1 upon reaching the monotectic temperature. The latent heat of the monotectic reaction is added to phase L1. L2 droplets appearing at the monotectic reaction front are modeled to be entrapped in the monotectic matrix by applying a similar enlarged viscosity at or below the monotectic point. Additional assumptions are as follows:
Two different simulations are made: one without gravity force and one with gravity force. The results of them are shown in Figure 8 and Animation 4. The multiphase model results presented here, with accompanying animations, help to visualize the different flow and sedimentation phenomena and their impact on the formation of macrosegregation. Multiphase modeling provides a deeper insight in several relevant macrosegregation phenomena. The models discussed here may be considered preliminary and qualitative in nature as a result of the model assumptions and simplifications, thus some of the simulation results may not be suitable for quantitative comparisons with industry processes. Future work, however, will include the necessary refinements required to successfully create a multiphase model compatible with industrial castings. This work was partially sponsored by the Christian-Doppler Society, Austria, in the framework of CD Laboratory-Multiphase Simulation of Metallurgical Processes, and partially supported by the ESA-MONOPHAS project–Advanced Bearing Alloys from Immiscible with Aluminum.
1. M.C. Flemings, “Our Understanding of Macrosegregation: PAST and Present,” ISIJ Int., 40 (9) (2000), pp. 833–841. Menghuai Wu and Andreas Ludwig are with the Department of Metallurgy at the University of Leoben in Austria. |