TMS QUICK LINKS:
  • TMS ONLINE
  • MEMBERS ONLY
  • MEMBERSHIP INFO
  • MEETINGS CALENDAR
  • PUBLICATIONS

JOM QUICK LINKS:
  • JOM HOME PAGE
  • MORE HTML ARTICLES
  • COMPLETE ISSUES
  • BOOKS REVIEWS
  • SUBSCRIBE

Oscillation marks accompanied by sub-surface hooks routinely appear on the surface of continuously cast steel slabs, and are especially severe in ultra-low-carbon steel. This article presents a new detailed mechanism for their formation, which has been developed by combining existing theoretical modeling results, experimental observations, and analyses based on optical and scanning-electron microscopy. Hooks form by solidification and dendritic growth at the liquid meniscus during the negative strip period. Oscillation marks are generated when molten steel partially overflows over the frozen meniscus shortly afterward and incompletely fills in the gap before solidifying. The results are presented in the form of a graphical animation of the various events occurring near the meniscus that lead to the formation of these defects.

BACKGROUND

The surface quality of continuous-cast steel slabs is greatly affected by oscillation marks^1,2 and sub-surface hook³ formation, which lead to cracks and slivers in the final rolled product. Oscillation marks are transverse depressions (Figure 1a) running around the strand perimeter that form during each vertical oscillation of the mold. Periodic mold oscillation is needed to prevent sticking of the solidifying shell to the mold walls. Providing a “negative strip time” period in each oscillation cycle, when the mold moves downward faster than the casting speed, also encourages infiltration of the mold slag into the gap between the mold wall and steel shell.

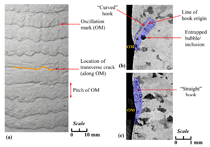
A “hook” is a distinct sub-surface microstructural feature^4–6 that often accompanies an oscillation mark, depending on the steel grade and casting conditions.⁷ Hooks increase in severity with decreasing carbon content, slow oscillation, and low casting speed. Hooks tend to entrap mold slag, floating inclusions, and gas bubbles that often lead to surface defects such as slivers and blisters^8,9 during subsequent rolling processes. Examples of typical “curved hook” and “straight hook” shapes are shown (shaded in blue) in Figure 1b and c, respectively.^4,5 In extreme cases, the entire slab surface must be ground⁴ to remove oscillation marks, hooks, and associated defects completely, leading to higher cost and lower productivity and yield.

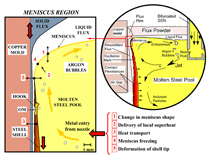
Hooks and oscillation marks form due to many complex interacting physical phenomena that vary with time near the meniscus where the molten steel surface meets the mold wall, as illustrated in Figure 2. Pressure fluctuations in the liquid slag channel due to mold oscillation alter the meniscus shape. The turbulent flow patterns in the mold cavity bring liquid to the meniscus region with varying amounts of transient momentum and superheat. Heat is conducted from the solidification front to the mold through the steel shell, and liquid and re-solidified slag layers. The meniscus region might solidify, depending on the local superheat of the liquid, the availability of nuclei sites, the ease of nucleation and growth, and alloy properties such as freezing range. The mold or slag rim may interact with the meniscus and shell during the negative strip period, especially if it is large. Rapid changes in temperature gradient may cause thermal distortion of the shell tip, which depend on the steel mechanical properties and the extent of level fluctuations relative to the shell tip. These events together determine the shape and size of sub-surface hooks and their corresponding oscillation marks.

Many different conflicting mechanisms for the formation of oscillation marks and hooks have been proposed in the past. They can be grouped into three general categories:

• Discontinued shell growth-based mechanisms:^10–12 Sticking to the mold wall during initial solidification disrupts steel shell growth. Subsequent solidification heals the disjointed shell edges, creating an oscillation mark.
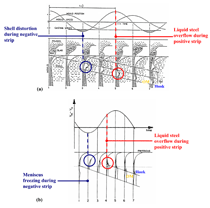
• Shell bending and overflow-based mechanisms:^3,13–15 The initial shell tip is forced to deform and bend away from the mold surface during the negative strip period. The causes of bending include viscoplastic thermal deformation,¹³ sudden level drop,^14,16 and mechanical interaction between the slag rim and shell tip.³ Subsequent overflow of liquid steel over the curved shell surface during positive strip period simultaneously creates a hook and oscillation mark. This mechanism is illustrated in Figure 3a.¹⁵
• Meniscus solidification and overflow-based mechanisms:^1,7,17–19 The curved meniscus solidifies during the negative strip period. Subsequent overflow over this frozen meniscus during the positive strip period forms the hook and its associated oscillation mark. This mechanism is shown in Figure 3b.¹

The first group of mechanisms is likely to occur during billet casting with oil lubrication, where the steel shell can directly contact and stick to the bare mold surface. However, during continuous casting with mold powder, a stable layer of liquid and re-solidified slag is usually present between the steel shell and mold surface, preventing direct shell-mold contact. Additionally, there is no evidence of hot tearing or welding in the micrographs presented in Figure 1. This mechanism therefore is not responsible for hook-type oscillation mark formation, at least for the ultra-low-carbon steel slab samples of interest in this work.

The second group of mechanisms includes two independent theories for hook formation prior to overflow: mechanical bending of the initial shell tip or thermal distortion. Bending seems unlikely because mechanical forces transmitted through the liquid layer would be too small to bend the steel into the exact shape of a frozen meniscus. Such large strains would likely fracture the shell tip anyway. The fragile hook is susceptible to hot tearing, as brittle fracture of a semi-solid metal needs only ~1% strain.²⁰ Indeed, Sengupta et al.^5,6 observed a separated hook tip near a truncated hook.⁶

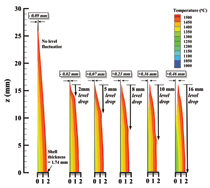
Thermal distortion of the shell tip was studied using a coupled thermal-stress model by Thomas and Zhu,¹⁴ who modeled a sudden level drop that exposed the inner edge of the shell to lower temperature. A shell tip deformation of ~1.65 mm was predicted for a severe level drop of ~20 mm, which occurs only rarely in an automated casting machine. Further work¹⁶ with this model has shown that the thermal distortion is much lower for more common but smaller (within ±10 mm²¹) level fluctuations, as shown in Figure 4. The maximum distortion of the shell was found to be only ~0.46 mm for a large level drop of 16 mm for 0.4 s. Although the shape of the shell tip is consistent with the hook shape near the surface, shown in Figure 1c, this mechanism alone cannot explain the deep hooks (up to ~2.5 mm)⁴ in Figure 1b that accompanied every one of a series of oscillation marks in ultra-low carbon steel slabs.⁴ This particular steel grade is well known to exhibit large hooks,^22,23 while oscillation marks are deepest in peritectic steels.

The third mechanism, meniscus freezing and overflow, is supported by recent metallographic investigations conducted on specially etched ultra-low carbon steel samples by J. Sengupta et al.⁶ which clearly revealed dendrites originating from several different nucleation sites located on or near the line of hook origin (see Figure 1b). This line was confirmed to be the instantaneous shape of the frozen meniscus, based on a reasonable match between measured curved hook shapes and the meniscus shape predicted by Bikerman’s equation.^24,25 Thus, meniscus freezing is responsible at least for the formation of curved hooks in ultra-low carbon steel.

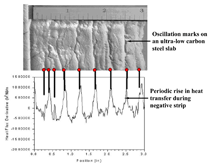
Recent experiments with a mold simulator by A. Badri et al.^26,27 revealed a consistent rise in heat flow into the mold near the meniscus region only during each negative strip period. The oscillation marks align with peaks in the heat flux curves, as shown in Figure 5, for an ultra-low carbon steel slab. This contradicts most previous mechanisms.

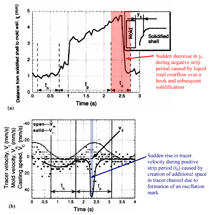
A sharp drop in the thickness of the channel between the solidified shell and the mold wall was observed during the negative strip period by K. Tsutsumi et al.,²⁸ as shown in Figure 6a. These researchers conducted experiments on an Sn-Pb alloy (metal) and stearic acid (slag) system to observe oscillation marks and mold powder infiltration behavior. In addition, a sudden rise in tracer velocity was measured in the stearic acid slag channel during the positive strip period, as indicated in Figure 6b.

The rest of this paper describes in detail a new mechanism of how hooks and oscillation marks form, which is consistent with these experimental observations. Increased understanding is achieved by creating real-time and slow-motion “intelligent” animations of the meniscus region during the oscillation cycle.

Previous hook and oscillation mark formation mechanisms have been presented only in a schematic format (e.g., Figure 3a and b) that obscures the real events. To address these issues, this work combines existing modeling results, experimental measurements, and plant observations together to construct an animation to illustrate events at the meniscus as accurately as possible. Specifically, the time-dependent positions of the mold, slag rim, solidifying shell, and meniscus are graphically tracked to visualize the formation of oscillation mark no. 1 in Figure 7. This figure shows three consecutive hook-type oscillation marks observed on an ultra-low carbon steel slab cast at Posco Gwangyang Works, South Korea.⁴ They are separated by ~8 mm, which is very close to the theoretical “pitch” of casting speed divided by oscillation frequency. The alloy composition and casting details are given in Table I. The variation of mold and shell velocity with time during the oscillation period is shown in Figure 8a, which reveals the negative and positive strip periods. The corresponding positions relative to the top liquid surface (i.e., in the laboratory frame of reference) are shown in Figure 8b.

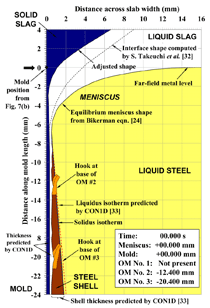
Each frame in the animation was created by systematically plotting the positions of the mold, meniscus, slag rim, solid shell, mold slag channel, hooks, and oscillation marks in x-z Cartesian space. The x-direction represents distance through the slab thickness, measured from x = 0 at the mold wall. The z-direction represents vertical distance along the strand/slab length. The first frame is shown in Figure 9, and corresponds to time, t = 0 s in Figure 8b. The z = 0 line indicates the mold position midway between oscillations and at t = 0, coincides with the far-field metal level in the mold, which is assumed to remain unperturbed at all times.

At t = 0, the mold acceleration is zero, as its mean position (z = 0) matches the far-field metal level. Thus, the positive pressure in the slag channel during the negative strip period from the previous cycle is assumed to be completely released by the time the mold reaches the start of the next cycle. Thus, in the absence of surface waves and inertial forces, the meniscus shape in the first frame is at equilibrium, determined solely by the balance of surface tension and ferrostatic pressure forces given by Bikerman’s equation.^24,29 In calculating this shape, a surface tension of 1.6 N/m was chosen,³⁰ corresponding to the sulfur content of 0.01% (Table I), and the steel density was assumed be 7,000 kg/m³ at 1,560°C.

The position of the solid slag rim was extrapolated from the isothermal line at the solidification temperature of the slag in the temperature distribution computed by Takeuchi et al.³¹ Taking into account the differences in slag melting temperature (1,130°C³¹ vs. 1,145°C at Posco³²) and superheat (20°C³¹ vs. 32°C at Posco³²), the position of the solid slag rim during the plant trial was adjusted upward in constructing Figure 9.

The thicknesses of the liquid and re-solidified slag layers separating the shell and mold surfaces were computed using a one-dimensional finite-difference model, CON1D,³³ for the conditions of the plant trial (Table I). Computed thicknesses of 0.22 mm and 0.34 mm for liquid and solid slag layers were used in the “results” frames. The profile of the left edge of the slab including the oscillation marks and the hook shapes were traced from Figure 7. The thickness profile of the solid steel shell along the mold was also taken from computations with CON1D. The shell thickness at the bottom of the figure (~18 mm below the shell tip) is ~1.3 mm. In this way, Figure 9 was constructed by assembling together realistic data from many sources.

Each frame of the animation of events that form oscillation mark (OM) no. 1 was constructed by altering the preceding frame using logical scientific principles and the following constraints. The mold position is taken from Figure 8b. The solid slag rim was assumed to be attached to the mold wall (no-slip condition), so its profile shifts with time accordingly. The oscillation marks and hooks move down the left edge of the solid shell at the casting speed. The shell thickness profile is constant with time, except at the shell tip and opposite the hooks.

The meniscus shape changes due to pressure changes during the positive and negative strip periods. Dynamic effects near the meniscus that force its shape to deviate from the equilibrium shape during an oscillation cycle were first observed by T. Tanaka and K. Takatani,³⁴ on a silicon oil-water interface inside an oscillating acrylic mold. The meniscus flattens due to the positive pressure in the slag channel during the negative strip period and bulges outwards due to the negative pressure in the slag channel during the positive strip period. Thus, movement of the solid slag rim was assumed to vary the slag pressure and distort the meniscus appropriately. The instantaneous shape of the meniscus becomes the line of hook origin for OM no. 1 when it freezes. The hook growth from this line then evolves into hook shell thickness. As the shell moves downwards, OM no. 1 and its hook form and grow, while OM no. 3 gradually moves out of the frame of this Cartesian space.

In total, 36 “results” frames were constructed in Microsoft PowerPoint® 2003 to illustrate the phenomena occurring at the meniscus region during one oscillation cycle, in steps of 0.01 s for a total time of 0.345 s. The process of logically creating the figures while satisfying the many constraints revealed the specific events leading to the formation of a hook and oscillation mark. Frame numbers 1 through 36 were exported to a vector-graphics-based program such as Deneba Canvas® 9.0 to create graphics interchange format (GIF) files that were finally stitched together to produce a movie in audio-video interleave format (AVI) using RAD Video Tools™.

ANIMATION OF NEW MECHANISM

Hook and oscillation mark formation can be viewed in real time in Animation 1a. In real time, the events occur too fast to see clearly. Therefore, a slow-motion version (1/10th speed with high-resolution) is presented in Animation 1b, where the events occurring during each oscillation cycle can be studied more easily. A low-resolution version of this animation has also been presented in Animation 1c to enable faster downloading from the website.

The animations reveal how the mold moves upward together with the slag rim during the positive strip period between 0 s to 0.110 s (see Figure 8b). Thus, the gap between the far-field top-surface metal level and the solid slag rim gradually opens up, creating negative pressure on the curved meniscus. The meniscus bulges upward from its equilibrium shape, due to the combined effects of this negative pressure and the inertia imparted by the upward mold movement. The negative pressure draws liquid slag into the gap, thereby initiating mold slag consumption during this time. The rate of suction gradually decreases as the mold approaches its maximum height of +2.938 mm at 0.090 s. As the mold velocity decreases, the negative pressure is gradually neutralized by the slag inflow.

Eventually, the mold reaches its highest point and moves downward with increasing velocity, overtaking the speed of the solid shell after 0.110 s. This begins the negative strip period. The slag rim moving down with the mold builds up positive pressure near the meniscus, which pumps liquid slag out of the gap. Some of this liquid slag is pumped into the channel between the mold and shell. This contributes to mold slag consumption during this negative strip time and tends to push the shell slightly away from the mold. This lubrication effect facilitates smooth withdrawal of the solid shell from the mold, which is why the mold is oscillated.

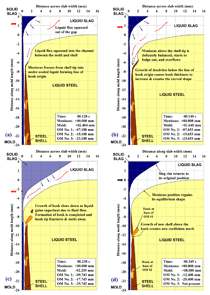
The first crucial event in the formation of hook no. 1 is meniscus freezing, which starts at 0.120 s and dictates the ultimate shape of this hook. This particular frame is shown in Figure 10a for the benefit of closer analysis. As the frozen meniscus travels downward with the casting velocity, the liquid meniscus continues to freeze (i.e., dendrites grow from the line of origin into the liquid steel, extending the hook). Until t = 0.140 s, the meniscus of heavy molten steel supported above the (new) shell tip is precariously balanced by surface tension.

This unstable situation soon triggers the second crucial event: the liquid steel overflows. Overflow occurs when inertial forces instantaneously exceed surface tension forces, as shown in Figure 10b. Although possible at any time during the cycle, this seems most likely shortly after the beginning of the negative strip period. The heavier liquid steel naturally falls into the interfacial channel, displaces some of the liquid mold slag, and melts through some of the solid mold slag layer. This brings undercooled liquid steel closer to the mold wall during the negative strip period. The heat transfer rate increases during this time due to the gradually decreasing thickness of the mold slag layer that separates the mold and the molten steel. The heat transfer rate is largest while the steel is still liquid, before solidification produces a surface roughness and solid layer that slows down heat transfer. This mechanism is consistent with experimental observations by Badri et al. that the maximum heat flux occurs during the negative strip time.^26,27 It also explains the shape of the slab surface, which is observed to bulge toward the mold wall just above the oscillation mark.⁵

The start of the overflow obviously dictates the maximum possible length of the hook. The contact angle stays constant as liquid flows over the top of the hook. The rapid heating of the cold side of the shell tip would also cause thermal expansion, slightly increasing hook curvature due to thermal distortion. The overflowing liquid is also likely to carry mold slag droplets, gas bubbles, inclusions, and other contaminants collected near the meniscus, which become entrapped just above the oscillation mark and hook, leading to defects.

For a short time, the colder hook is able to grow rapidly in both directions away from its line of origin. As the hook reheats, solidification naturally slows down, allowing inter-dendritic liquid and contaminants such as mold powder to concentrate between the gradually coarsening dendrite arms.⁶ Very soon, the hook growth stops. This explains the microstructural observations of Sengupta.⁶

During the overflow event, small inertial forces may fracture the tip from the hook by brittle hot tearing. This third crucial step in the mechanism, shown in Figure 10c, renders the typical truncated shape of the hook, as shown in Figure 1b. This explains the fractured hook tip observed by Sengupta.^5,6 Alternatively, the fractured tip is carried away by the incoming liquid steel and gradually melts, as shown in the animation.

The positive strip time period begins just before the mold reaches its lowest position in the oscillation cycle (i.e., –2.944 mm at 0.260 s). As the mold moves upward, the gap above the new metal meniscus that had been closing during negative strip starts to open up. The direction of slag flow reverses as the positive pressure is released. As the mold gains upward speed, the intake of slag into the gap increases and mold powder consumption continues to rise. Additionally, the meniscus shape is pulled up. This process also facilitates the beginning of conventional shell growth next to the mold, which is the fourth and final crucial event.

The oscillation mark accompanying hook no. 1 is created at this time, as the overflowing liquid steel incompletely fills the bottom of the interfacial gap. The extent of the penetration of liquid steel into filling the interfacial gap and re-melting the solid slag layer determines the final shape of the upper side of the oscillation mark. The liquid slag trapped during this event accounts for most of the slag consumption. The sudden rise in tracer velocity observed by Tsutsumi et al.²⁸ corresponds to the extra slag that is drawn in to refill the expanding gap region caused by the rise of the slag rim and mold during positive strip.

Normal solidification continues until 0.345 s, which ends the complete mold oscillation cycle. The first (Figure 9) and the last (Figure 10d) frames are the same, except that hooks 1 and 2 in the latter replace hooks 2 and 3 in the former. The animation runs continuously as all of the events described above are repeated periodically, producing a hook and oscillation mark during each mold oscillation cycle.

Obviously, chaotic events such as metal level fluctuations may occur at any time during the oscillation cycle and will alter the shapes of the resulting oscillation marks and hooks. These events can also create additional oscillation marks/surface depressions or alter their spacing, as seen in Figure 5, by triggering the overflow event at a different time during the cycle. Each overflow event naturally can create at most one hook.

After forming, the hook and its associated oscillation mark move down the mold at the casting speed. Hook nos. 1 and 2 stick out past the solidification front into the liquid. This allows the dendrites in the hook to further coarsen, before the shell eventually catches up, embeds the hooks, and solidification continues past. In addition to this, inclusions and argon bubbles circulating in liquid steel pool (refer to Figure 2) near the meniscus and ~15 mm below (for this case) can be easily entrapped by these protruding hooks. The events depicted in the animation clearly reveal the salient features of the new mechanism for hook and oscillation marks presented in this work. Further details and justification of the new mechanism are presented elsewhere.^4–6

This paper reveals the details of a new mechanism for the formation of hooks and oscillation marks during continuous casting of ultra-low carbon steel, with the aid of an animation generated from a series of carefully constructed schematics. These schematics simultaneously satisfy separate pieces of knowledge from several different sources. The animation presented in this paper allows easy visualization of the crucial events that govern formation of the as-cast surface and its associated features, which include hooks, oscillation marks, and other defects. This new fundamental understanding should ultimately lead to practices that will minimize or eliminate these surface defects.

The authors wish to thank the Natural Sciences and Engineering Research Council of Canada, the National Science Foundation (Grant DMI-04-23794), and the Continuous Casting Consortium at the University of Illinois at Urbana-Champaign for support of this project.

1. E. Takeuchi and J.K. Brimacombe, “The Formation of Oscillation Marks in the Continuous Casting of Steel Slabs,” Metallurgical Transactions B, 15B (1984), pp. 493–509.
2. E. Takeuchi and J.K. Brimacombe, “Effect of Oscillation-Mark Formation on the Surface Quality of Continuously Cast Steel Slabs,” Metallurgical Transactions B, 16B (1985), pp. 605–625.
3. T. Emi et al., “Influence of Physical and Chemical Properties of Mold Powders on the Solidification and Occurrence of Surface Defects of Strand Cast Slabs,” Proceedings of National Open Hearth and Basic Oxygen Steel Conference, 61 (1978), pp. 350–361.
4. H.-J. Shin et al., “Analysis of Hook Formation Mechanism in Ultra Low Carbon Steel using CON1D Heat Flow–Solidification Model,” Materials Science & Technology 2004 (Warrendale, PA: TMS and AIST, 2004), Vol. II, pp. 11–26.
5. J. Sengupta et al., “Mechanism of Hook Formation during Continuous Casting of Ultra-low Carbon Steel Slabs,” Metallurgical and Materials Transactions A, 37A (5) (2006), pp. 1597–1611.
6. J. Sengupta et al., “Micrograph Evidence of Meniscus Solidification and Sub-Surface Microstructure Evolution in Continuous-Cast Ultra-Low Carbon Steels,” Acta Materialia, 54 (4) (2006), pp. 1165–1173.
7. K. Bo et al., “Mechanism of Oscillation Mark Formation in Continuous Casting of Steel,” Journal of University of Science and Technology Beijing, 7 (3) (2000), pp. 189–192.
8. K.D. Schmidt et al., “Consequent Improvement of Surface Quality by Systematic Analysis of Slabs,” Steel Research International, 74 (11-12) (2003), pp. 659–666.
9. J.-P. Birat et al., “The Continuous Casting Mold: A Basic Tool for Surface Quality and Strand Productivity,” Steelmaking Conference Proceedings, 74 (1991), pp. 39–40.
10. E.S. Szekeres, “Overview of Mold Oscillation in Continuous Casting,” Iron and Steel Engineer, 73 (7) (1996), pp. 29–37.
11. R. Sato, “Powder Fluxes for Ingot Making and Continuous Casting,” Proceedings of National Open Hearth and Basic Oxygen Steel Conference, 62 (1979), pp. 48–67.
12. J. Savage and W.H. Pritchard, “Problem of Rupture of Billet in Continuous Casting of Steel,” Iron and Steel, 27 (14) (1954), pp. 649–652.
13. K. Schwerdtfeger and H. Sha, “Depth of Oscillation Marks Forming in Continuous Casting of Steel,” Metall. Mater. Trans. B, 31B (2000), pp. 813–826.
14. B.G. Thomas and H. Zhu, “Thermal Distortion of Solidifying Shell Near Meniscus in Continuous Casting of Steel,” Solidfication Science and Processing, ed. I. Ohnaka and D.M. Stefanescu (Warrendale, PA: TMS, 1996), pp. 197–208.
15. H. Tomono, “Elements of Oscillation Mark Formation and Their Effect on Transverse Fine Cracks in Continuous Casting of Steel” (Ph.D. Thesis, Federal Institute of Technology, 1979).
16. J. Sengupta and B.G. Thomas, “Effect of a Sudden Level Fluctuation on Hook Formation During Continuous Casting of Ultra-Low Carbon Steel Slabs,” Modeling of Casting, Welding, and Advanced Solidification XI, ed. C.A. Gandin and J.E. Allison (Warrendale, PA: TMS, 2006), pp. 727–236.
17. I.G. Saucedo, “Early Solidification during the Continuous Casting of Steel,” Steelmaking Conference Proceedings (Warrendale, PA: ISS-AIME, 1991), pp. 43–53.
18. H. Yamamura, Y. Mizukami, and K. Misawa, “Formation of Solidified Hook-like Structure at the Subsurface in Ultra Low Carbon Steel,” ISIJ International (Supplement), 36 (1996), pp. S223–226.
19. O. Putz, O. Breitfeld, and S. Rodl, “Investigations of Flow Conditions and Solidification in Continuous Casting Moulds by Advanced Simulation Techniques,” Steel Research, 74 (11-12) (2003), pp. 686–692.
20. H. Mizukami, A. Yamanaka, and T. Watanabe, “High Temperature Deformation Behavior of Peritectic Carbon Steel during Solidification,” ISIJ International, 42 (9) (2002), pp. 964–973.
21. W. Lai, M. Milone, and I.V. Samarasekera, 83rd Steelmaking Conference Proceedings (Warrendale, PA: ISS-AIME, 2000, pp. 261–274.
22. Y. Kitano, “Improvement of Slab Surface Quality of Ultra-Low Carbon Steel,” Tetsu-To-Hagane, 80 (1994), pp. T165–168.
23. M. Suzuki, “Initial Solidification Behaviour of Ultra Low Carbon Steel,” CAMP-ISIJ, Vol. 11 (1998), pp. 42–44.
24. J.J. Bikerman, Physical Surfaces (New York: Academic Press, Inc., 1970).
25. I. Jimbo and A.W. Cramb, “Calculations of the Effect of Chemistry and Geometry on Free Surface Curvature during Casting of Steels,” Iron & Steelmaker, 20 (6) (1993), pp. 55–63.
26. A. Badri et al., “A Mold Simulator for the Continuous Casting of Steel: Part I. The Development of a Simulator,” Metallurgical & Materials Transactions B, 36B (2005), pp. 355–371.
27. A. Badri et al., “A Mold Simulator for Continuous Casting of Steel: Part II. The Formation of Oscillation Marks during the Continuous Casting of Low Carbon Steel,” Metallurgical & Materials Transactions B, 36B (2005), pp. 373–383.
28. K. Tsutsumi, J. Ohtake, and M. Hino, “Inflow Behavior Observation of Molten Mold Powder between Mold and Solidified Shell by Continuous Casting Simulator Using Sn-Pb Alloy and Stearic Acid,” ISIJ International, 40 (2000), pp. 601–608.
29. H. Fredriksson and J. Elfsberg, “Thoughts about the Initial Solidification Process during Continuous Casting of Steel,” Scandinavian Journal of Metallurgy, 31 (2002), pp. 292–297.
30. J. Lee and K. Morita, “Evaluation of Surface Tension and Adsorption for Liquid Fe-S Alloys,” ISIJ International, 42 (6) (2002), pp. 588–594.
31. S. Takeuchi et al., “Control of Oscillation Mark Formation during Continuous Casting,” Steelmaking Conference Proceedings (Warrendale, PA: ISS-AIME, 1991), pp. 37–41.
32. H.-J. Shin et al, “Effect of Mold Oscillation on Powder Consumption and Hook Formation in Ultra-Low Carbon Steel Slabs,” AISTech 2004 Iron & Steel Technology Conference Proceedings Vol II (Warrendale, PA: The Association for Iron & Steel Technology, 2004), pp. 1157–1170.
33. Y. Meng and B.G. Thomas, “Modeling Transient Slag Layer Phenomena in the Shell/Mold Gap in Continuous Casting of Steel,” Metallurgical & Materials Transactions B, 34B (2003), pp. 707–725.
34. T. Tanaka and K. Takatani, “Hydrodynamics of Molten Powder in the Vicinity of Meniscus in Continuous Casting,” CAMP-ISIJ, 2 (1989), p. 1263.

Joydeep Sengupta is a senior researcher with Dofasco Research & Development in Hamilton, Ontario, Canada. Brian G. Thomas is a professor in the Department of Mechanical Science and Engineering at the University of Illinois at Urbana-Champaign.

For more information, contact Brian G. Thomas, University of Illinois at Urbana-Champaign, Department of Mechanical Science and Engineering, 1206 West Green Street, Urbana, IL 61801; (217) 333-6619; fax (217) 244-6534; e-mail bgthomas@uiuc.edu.